曼德博集合|最直观的数学之美——用Python看到“上帝的指纹”

1. 关于曼德博集合的简单介绍：

曼德博集合（Mandelbrot set，或译为曼德布洛特复数集合）是一种在复平面上组成分形的点的集合，以数学家本华·曼德博的名字命名。曼德博集合与朱利亚集合有些相似的地方，例如使用相同的复二次多项式来进行迭代。
将曼德博集合无限放大都能够有精妙的细节在内，而这瑰丽的图案仅仅由一个简单的公式生成。因此有人认为曼德博集合是“人类有史以来做出的最奇异、最瑰丽的几何图形”，曾被称为“上帝的指纹”。

---

这是引自百度百科的一段介绍。总而言之，曼德博集合的发现使我们能以最直观的方式看到所谓的“数学之美”。

---

2. 如何获得曼德博集合：

从上一段介绍中，我们知道首先曼德博集合是定义在复平面上的。实际上关于复数概念，我们可以把它看作一种将(x,y)两个变量用一个复变量z代替的简单写法，无需顾虑太多。其次，曼德博集合是通过一个迭代方程以及一些分类规则获得的点的集合，我们来考虑这些问题。

曼德博集合使用到的简单的迭代方程如下：

其中，z是复数变量，c是一个复数常量，而非我们通常见到的实数常量。
我们从z = 0开始对这个函数进行迭代，即

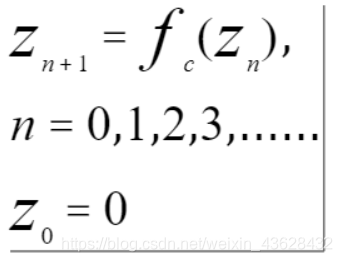
上面这个迭代公式最终可能趋近于无穷大，也可能趋近于某一个收敛值，这取决于复数常量c。所以，我们将所有可以产生收敛值的c归为一类，用某种颜色的点把它们都绘制出来，另一类产生无限大的c则用另一种颜色绘制。通过这几个简单的步骤，我们就能得到“上帝的指纹”——曼德博集合。

借助于计算机，我们将尝试进行这一过程。

---

3. 一些基础知识：

由于曼德博集合需要进行迭代，如果我们使用简单的方法进行计算的话（可能要用到许多层循环），既存在运行时间过长的问题，而且绘制的图形通常比较粗糙。为了快速获得漂亮的图形，我们将使用到NumPy来对计算过程进行矢量化，也就是在计算过程中加入矩阵表示。

下面介绍一些在编程方面的有用知识以及一些数学内容。

---

(1). 绘图必备——函数meshgrid()：

在使用matplotlib进行绘图时，需要传入x和y的坐标值，而通常情况下我们使用向量来进行（也就是使用列表），比如说

import matplotlib.pyplot as plt

plt.figure()
plt.plot([1,2,3],[1,2,3],marker='.',linestyle='')
plt.show()

通过设置参数，我们将得到三个散点，如图：

但是，我们的画布是二维的，如果能使用二维数组传递坐标值，我们将方便的多。matplotlib也为我们提供了支持：

import matplotlib.pyplot as plt

plt.figure()
plt.plot([[1,2,3],[1,2,3],[1,2,3]],[[1,1,1],[2,2,2],[3,3,3]],marker='.',linestyle='')
plt.show()

通过具有平面结构的二维数组，我们更加直观的绘制了这些点：

在上面的例子中，传递坐标值时，我们使用的是矩阵而不是简单的列表。

这样的二维矩阵，我们把它称为坐标矩阵，而meshgrid()就是在需要绘制大量点，而这些点的平面位置有一点规律（比如网格点）时用来帮助我们生成这样的坐标矩阵的。

我们通过使用这个函数绘制上一幅图，来看看这个函数的用法：

import matplotlib.pyplot as plt
import numpy as np

plt.figure()
X,Y = np.meshgrid([1,2,3]