数理方程与特殊函数|波动方程：杆的纵振动方程

---

考虑一均匀细杆，沿杆长方向作小振动。假设在垂直杆长方向的同一截面上各点的振动情况（即位移）完全相同，那么，这个位移是空间位置与时间的函数。

我们令任意时刻t此截面相对于平衡位置的位移为u(x, t)，取杆长方向为x轴方向，垂直于杆长方向的各截面均用它的平衡位置x标记，在杆中隔离出一小段(x, x + dx)，通过截面x，受到弹性力P(x, t)·S的作用，其中P(x, t)为单位面积所受的弹性力，即应力，方向沿x方向为正。同样的，通过截面x + dx，微元也受到弹性力P(x + dx, t)·S的作用。

我们将重力忽略，可以得到方程

我们通过dm进行一步变化：

这个方程中，P是未知的。所以，我们要继续寻找P的方程。

---

如果略去垂直干长方向的形变，根据Hooke定理，应力P与应变（相对位移）δu / δx成正比，即

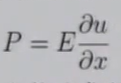
E即为杨氏(Young)模量，是一个物质常数。

---