图算法二 —— 单源最短路径（Bellman-Floyd算法、SPFA算法、Dijkstra算法）

最新推荐文章于 2024-05-19 16:50:57 发布

L☆★

最新推荐文章于 2024-05-19 16:50:57 发布

阅读量608

点赞数

分类专栏： # 图文章标签：算法图论数据结构

本文链接：https://blog.csdn.net/weixin_43662553/article/details/125001127

版权

图专栏收录该内容

3 篇文章 0 订阅

订阅专栏

文章目录

单源最短路径

单源最短路径

Bellman-Floyd 算法

算法描述

需要一个一维数组dist[]来存储每个点到起点的距离，设起点为S，终点为D，那这条最短路径一定是 S->p1->p2->...->D的形式。

思想上和上述的算法保持一致，就是暴力解法

你想求出某点到其他所有点的最短路径：

第一次遍历，你求得固定点一步可以到达的点的结果，其余点结果为知；
第二次遍历，你求得固定点两步可以到达的点的结果；
……
只要图中不存在环，你遍历节点个数-2次，一定会得到所有的最短路径结果。这里用的是链式前向星存图。

实现代码

void Bellman_floyd(int n, int m) {
    for (int j = 0; j < n - 1; j++) {
        for (int i = 1; i <= m; ++i) {
            dist[edges[i].to] = min(dist[edges[i].to], dist[edges[i].from]) + edges[i].w;
        }
    }
}

SPFA 算法（ Shortest Path Faster Algorithm ）

算法描述

观察发现，Bellman-Floyd算法第一次遍历时，可能更新的点只有S可以直接到达的点；

然后下一次遍历可能被更新的只可能是S能直接到达的点能直接到达的点。

SPFA算法正是利用这种思想，并进行优化。

借用队列这一数据结构，在每次对点操作时更新它能到达的点，并把队列中不存在的点加入队列，并出队操作结束的点，这样直到队列为空，也就满足了要求。

然而，该方法的时间复杂度不稳定，和上一种算法的思路是相同的，因此在最坏的情况下，时间复杂度为 $O (m n)$

题目

给定一个n个点m条边的有向图，图中可能存在重边和自环， 边权可能为负数。

请你求出1号点到n号点的最短距离，如果无法从1号点走到n号点，则输出impossible。

数据保证不存在负权回路。

输入格式

第一行包含整数n和m。

接下来m行每行包含三个整数x，y，z，表示存在一条从点x到点y的有向边，边长为z。

输出格式

输出一个整数，表示1号点到n号点的最短距离。

如果路径不存在，则输出”impossible”。

数据范围

1≤n,m≤10^5

图中涉及边长绝对值均不超过10000。

输入样例：

输出样例：

python 代码实现

 
n, m = map(int, input().split())
idx = 0
h = [-1]*(n+1)
e, ne, w = [0]*(2*m+1), [0]*(2*m+1), [0]*(2*m+1)
dist = [float('inf')]*(n+1)
def add(a, b, wei):
    global idx
    e[idx], w[idx] = b, wei
    h[a], ne[idx] = idx, h[a]
    idx += 1
 
def spfa():
    queue = [1]
    st = [False]*(n+1) # 用来判断当前点是否在队列中
    dist[1] = 0
    hh, tt = 0, 0
    while hh <= tt:
        t = queue[hh]; hh += 1
        st[t] = False
        i = h[t]
        while i != -1:
            j, wei = e[i], w[i]
            if dist[j] > dist[t] + wei:
                dist[j] = dist[t] + wei
                if not st[j]:
                    queue.append(j)
                    st[j] = True
                    tt += 1
            i = ne[i]
for _ in range(m):
    a, b, wei = map(int, input().split())
    add(a, b, wei)
 
spfa()
if dist[n] == float('inf'): print('impossible')
else: print(dist[n])

c++ 代码实现

void SPFA(int s) //s为固定点编号， inqueue数组判断节点是否在队列中
{
    queue<int> Q;
    Q.push(s);
    while (!Q.empty()) {
        int p = Q.front();
        Q.pop();
        inqueue[p] = 0;
        for (int e = head[p]; e != 0; e = edges[e].next) {
            int to = edges[e].to;
            if (dist[to] > dist[p] + edges[e].w) {
                dist[to] = dist[p] + edges[e].w;
                if (!inqueue[to]) {
                    inqueue[to] = 1;
                    Q.push(to);
                }
            }
        }
    }
}

Dijkstra 算法

算法思想

Dijkstra算法基于一种贪心的思想，我们假定有一张没有负边的图。

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中
在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。
此外，每个顶点对应一个距离，S中的顶点的距离就是从v到此顶点的最短路径长度，U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。

例子

重点需要理解这句拗口的"按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度"

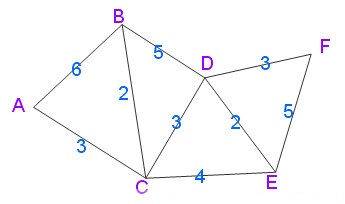
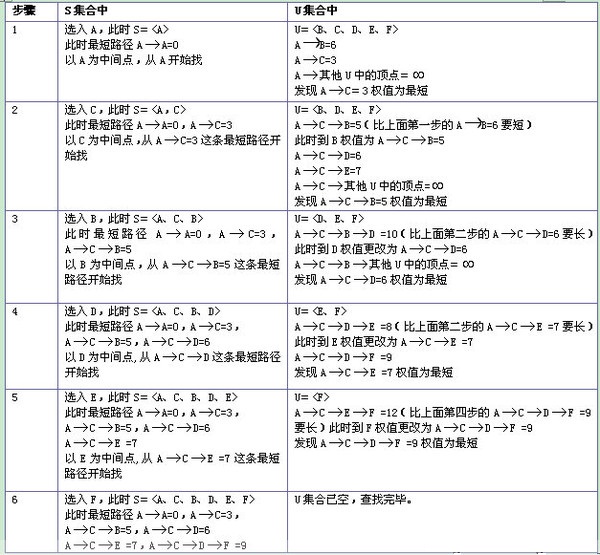
实际上，Dijkstra 算法是一个排序过程，就上面的例子来说，是根据A到图中其余点的最短路径长度进行排序，路径越短越先被找到，路径越长越靠后才能被找到，要找A到F的最短路径，我们依次找到了

A --> C 的最短路径 3
A --> C --> B 的最短路径 5
A --> C --> D 的最短路径 6
A --> C --> E 的最短路径 7
A --> C --> D --> F 的最短路径 9
Dijkstra 算法运行的附加效果是得到了另一个信息，A到C的路径最短，其次是A到B, A到D, A到E, A到F

再举一例，初点a到b最短有权10，b到c有权50，a到d有权30，d到c有权20，求a到c的最短路径。

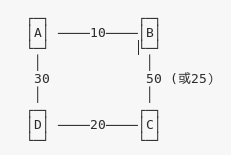
dijkstra

迪杰斯特拉算法的运行过程是一个排序的过程，既不是深度优先也不是广度优先算法。

根据A->某个点权值最小来判断下一个点是哪个点

就这个简单的例子而言，a和b都被加入S集合后，这时下一个要加入S集合结点，并不一定是c节点。 请把a和b节点组成的集合作为一个整体来考虑，当算法运行到 a和b 都被加入S集合后，你甚至都可以把 a 和 b在图中去掉用一个虚拟的s节点来表示，a 和 b 作为一个整体后，和这个整体相连接的边，最短的就是 a 到 d 这条边，但是，这时并不能直接因为这条边的权最小就将d 加入 S 集合；现在，再来假设 b 到 c的权不是50，而是25；现在和 S 集合相连接的边有a到d 30， b到c 25；这时，b到c的权值最小，但却不能加入S集合，因为 a 到 b 再到 c的权是 10 + 25 已经大于 a 到 d的权 30，所以 d 应该加入 S 集合，而不是 c；如果b 到 c的权值小于20，就是 c先加入 S 集合，而不是 d 了； b 到 c的权值恰好等于20，那么随便，先把d加入 S 还是先把 c 加入 S，都是一样的，没有区别。

另外，任意一点k，加入s集合后，就已经找到了从源点a到k的最短路径，前提条件是图中不能有带负数的权值边。我这样表述可以让算法更清楚，还是这个例子， a和b都被选入 S 集合后，去更新整个图，把a和b都去掉，用新节点 s 代替a和b，s 到 d 有权30， s 到 c 有权 10+50，下一步该选哪个节点并入 S 集合一目了然了吧。 d点选入 S 集合后，再把d点从图中抹去，更新虚拟的节点 s到c的权

C++ 代码实现

⾸先写⼀个结构体,⽤于保存最短距离和节点编号。

struct Polar {
    int dist, id;
    Polar(int dist, int id): dist(dist), id(id) {}
};

然后确定

struct cmp {
    bool operator()(Polar a, Polar b) { // 重载 ()运算符，使其称为一个仿函数
        return a.dist > b.dist;            // 这里是大于，使得距离短的先出队
    }
};
priority_quene<Polar, vector<Polar>, cmp> Q; // 小堆顶
int vis[n];    // 建立是否访问过的节点判断数组

算法实现：

void Dij(int s) {
    dist[s] = 0;
    Q.push(Polar(0, s));
    while(!Q.empty()) {
        int p = Q.top().id;
        Q.pop();
        if (vis[p])
            continue;
        vis[p] = 1;
        for (int e = head[p]; e != 0; e = edge[e].next) {
            int to = edges[e].to;
            dist[to] = min(dist[to], dist[p] + edges[e].w);
            if (!vis[to])
                Q.push(Polar(dist[to], to));
        }
    }
}

怎样打印路径？

只需要建立一个pre数组，在更新dist时候更新pre即可。由于算法最后的结果是一棵树，因此数组中保存此编号节点的父节点即可。每条路有且仅有一个祖先节点，一步步溯源上去的路径是唯一的。

python 代码实现

 
class Dijkstra:
    def __init__(self, graph, goal):
        self.graph = graph
        self.goal = goal
        self.open_list = {}
        # open_list初始化为一个空字典，keys为节点'1''2'...,values为distance即从'1'到该点的实际代价
        self.closed_list = {}
        # closed_list初始化为一个空字典，键和值与open_list相同
        self.open_list['1'] = 0
        # 因为我们初始节点为'1'，并且'1'到'1'的值为0,将其传入open_list列表中
        self.parent = {'1': None}
        # 初始父节点为字典型，初始键为'1'值为None，其中键是子节点，值是父节点
        self.min_dis = None
        # 初始最短路径长度为None
 
    def shortest_path(self):
 
        while True:
            if self.open_list is None:
                print('搜索失败， 结束！')
                break
 
            distance, min_node = min(zip(self.open_list.values(), self.open_list.keys()))  # 取出距离最小的节点
            self.open_list.pop(min_node)  # 将其从 open_list 中去除
 
            self.closed_list[min_node] = distance  # 将节点加入 closed_list 中
 
            if min_node == self.goal:  # 如果节点为终点
                self.min_dis = distance
                shortest_path = [self.goal]  # 记录从终点回溯的路径
                father_node = self.parent[self.goal]
                while father_node != '1':
                    shortest_path.append(father_node)
                    father_node = self.parent[father_node]
                shortest_path.append('1')
                print(shortest_path[::-1])  # 逆序
                print('最短路径的长度为：{}'.format(self.min_dis))
                print('找到最短路径， 结束！')
                return shortest_path[::-1], self.min_dis  # 返回最短路径和最短路径长度
 
            for node in self.graph[min_node].keys():  # 遍历当前节点的邻接节点
                if node not in self.closed_list.keys():  # 邻接节点不在 closed_list 中
                    if node in self.open_list.keys():  # 如果节点在 open_list 中
                        if self.graph[min_node][node] + distance < self.open_list[node]:
                            self.open_list[node] = distance + self.graph[min_node][node]  # 更新节点的值
                            self.parent[node] = min_node  # 更新继承关系
                    else:  # 如果节点不在 open_list 中
                        self.open_list[node] = distance + self.graph[min_node][node]
                        # 计算节点的值，并加入 open_list 中
                        self.parent[node] = min_node  # 更新继承关系
 
 
if __name__ == '__main__':
    g = {'1': {'2': 2, '3': 1, '4': 4},
         '2': {'4': 3, '6': 2},
         '3': {'5': 3},
         '4': {'6': 1},
         '5': {'4': 4, '6': 2}
         }
    goal = '6'
    dijk1 = Dijkstra(g, goal)