多米诺骨牌——变形版0,1背包问题

1、题目描述

多米诺骨牌有上下2个方块组成，每个方块中有1~6个点。现有排成行的上方块中点数之和记为S1，下方块中点数之和记为S2，它们的差为|S1-S2|。

例如在下图中，S1=6+1+1+1=9，S2=1+5+3+2=11，|S1-S2|=2。每个多米诺骨牌可以旋转180°，使得上下两个方块互换位置。 编程用最少的旋转次数使多米诺骨牌上下2行点数之差达到最小。

对于图中的例子，只要将最后一个多米诺骨牌旋转180°，可使上下2行点数之差为0。

输入格式
输入文件的第一行是一个正整数n(1≤n≤1000)，表示多米诺骨牌数。接下来的n行表示n个多米诺骨牌的点数。每行有两个用空格隔开的正整数，表示多米诺骨牌上下方块中的点数a和b，且1≤a，b≤6。

输出格式
输出文件仅一行，包含一个整数。表示求得的最小旋转次数。

输入输出样例
输入
4
6 1
1 5
1 3
1 2
输出
1

2、问题分析

这道题刚拿到手时不知道是个什么类型的题目，虽说这道题目被归类在线性动归模块里，但一开始看着有点像贪心，搞了一下，才20来分。。。。于是才想到用动态规划,但用动态规划吧，又比较麻烦，如果不是自己熟悉的那几个套路，就得自己定义状态、求状态转移方程、考虑边界、后效性等问题…而且一顿操作过后，如果发现自己搞错了，比如其实是一道区间动归的问题，但在那用线性思想搞了半天,最后才得个50分。。。那就是真的炸了。。

所以,我决定,下次不管遇到啥问题,能用数学思想建模的，通通先用数学思想建模。先把路子摸透了再开干,避免走些弯路。。。（谁叫计算机学的鼻祖是数学呢？两位公认的计算机学之父:艾伦·图灵，冯·诺依曼,可都是数学家)

因此,这道题目也不例外,直接用数学思想把它先摸透~

就这道题目而言吧,我管它有多少个骨牌呢,我先从1个开始考虑,设这个骨牌上端的值为a,下端的值为b,则它的差值就是a-b,(题目要求加绝对值,那为了避免一开始差值就出现负数,我就先设目前以及接下来出现的骨牌上端的值都大于下端的值)

接下来的推论如下图所示:

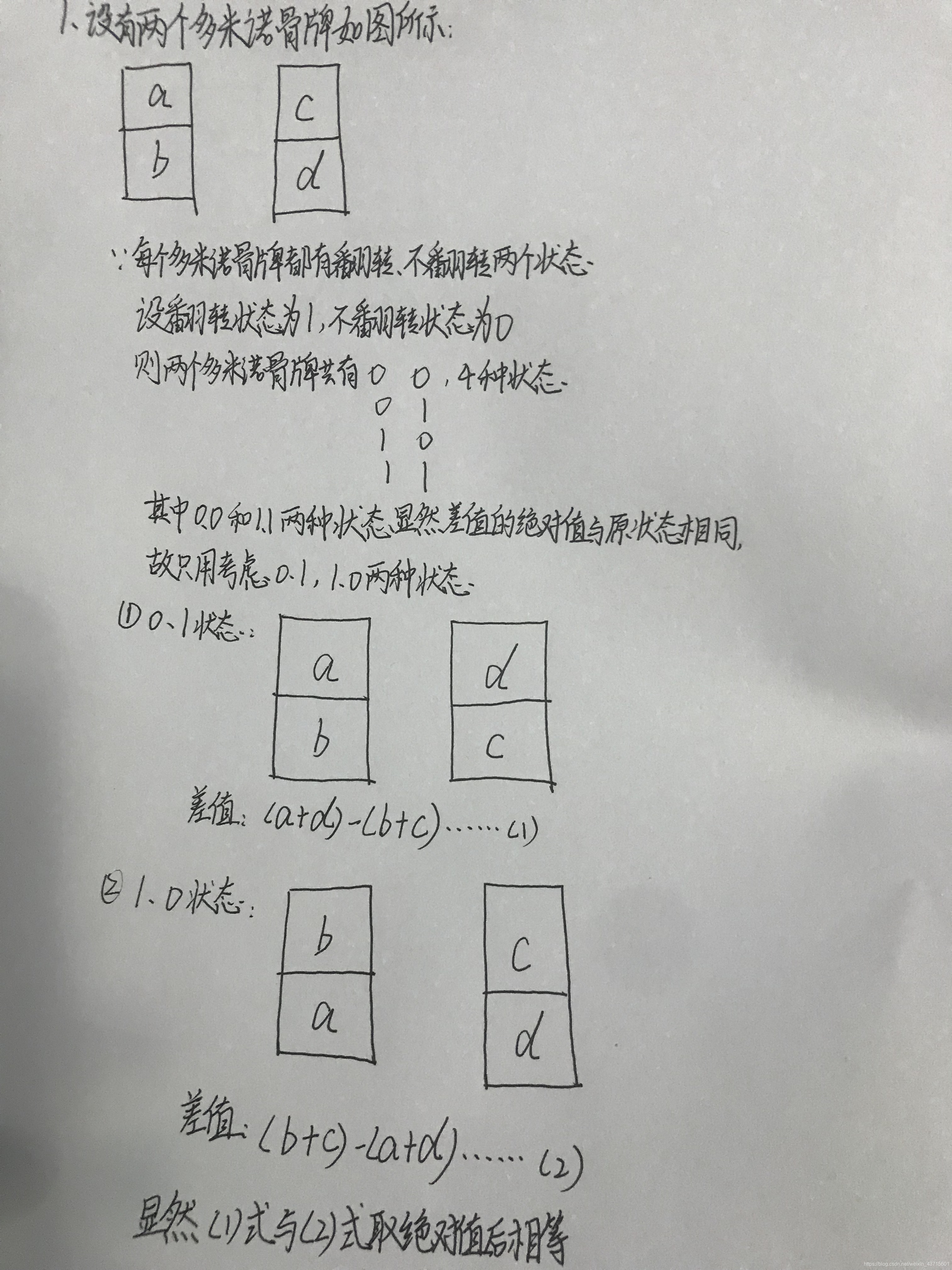
推到这里说明了啥？说明了如果动归来做是可行的,因为解决了无后效性问题，什么是无后效性呢？

无后效性是指如果在某个阶段上过程的状态已知，则从此阶段以后过程的发展变化仅与此阶段的状态有关，而与过程在此阶段以前的阶段所经历过的状态无关。利用动态规划方法求解多阶段决策过程问题，过程的状态必须具备无后效性。

因为动态规划一般都是从前往后推，求最优解，所以无后效性通俗点说就是求某个状态的最优解时,该状态的最优解只和当前状态与前一阶段计算的最优解有关,而与前一阶段的过程无关。

我这里计算的0,1状态和1,0状态差值无异说明：就算如果我是计算n个骨牌,我只需要从第一个骨牌开始推,将第一个骨牌的状态固定为0,后面根据第一个骨牌开始求解递推出了加上k个骨牌的最优解,我将这k+1个骨牌共同看做一个整体,这个整体的状态为0,而求解后面的n-k-1骨牌时,我只需要考虑引入它们后对当前状态的影响以及前面整体的状态即可。

搞到目前目前为止,还只解决了第一个问题，就是可以用动态规划解决这道题,但具体怎么搞,还是得再推几个栗子。

但显然这道题目中要考虑翻转的次数，因而我们开始建模，设n个物品分别为n个多米诺骨牌,每个物品的体积v[i]为每个多米诺骨牌上下点数差值的两倍，每个物品的重量w[i]为每个多米诺骨牌初始状态的翻转次数,背包的容量V为每个多米诺骨牌上下点数差值之和，便将问题转化为了一个背包问题，而考虑到每个物品只能取1次，因而便转换成了一个0-1背包问题。

对于这个0-1背包问题，我们思考的问题是如何使得背包内的物品体积v[i]之和尽可能大的情况下,物品的重量w[i]之和尽可能的小。

因此，尽管我们前面进行了一系列的操作，但依旧还存在两个需要考虑的问题:
(1)、如何定义w[i],即每个多米诺骨牌初始状态的翻转次数。
(2)、如何求解使得体积尽可能大的状态下重量之和最小的0-1背包问题。

对于第一个问题，个人认为还是比较好解决的。因为我上面的推论都建立在一个前提下——每个多米诺骨牌初始状态时上端点数大于下端点数,因此,初始时多米诺骨牌的翻转次数可定义为背包的初始重量,相当于一开始我便把它们装进了背包内。但在后续过程中若我发现了它们中某些多米诺骨牌一开始还是不装进去更好，我也可以把它们取出来(就相当于没装,1+(-1)=0)。因此，这些一开始就为使上端点数大于下端点数而被翻转的多米诺骨牌的初始重量设置为-1，而一开始未被翻转的多米诺骨牌的初始重量设置为1。

对于第二个问题,个人认为稍微有点难度,因为背包模板题里大多都是求价值之和最大的问题,求价值之和最小的问题比较少见。原因是用动态规划解决问题时定义的状态数组dp一般被定义在全局变量区内,或被初始化边界值为0,然而,根据这些边界值求最大值时,题目给的数据一般不会是负数,所以用0作为dp数组的边界值,一般也能求解正确，问题也不是很大。但求最小值的时候,问题就比较严重了,因为题目一般所给的数据都是正数,如果此时定义dp数组边界的值还是0,那用状态方程求解的很多状态,都会是错误的,可能都是0,0,0…因此,用动态规划解题时,很重要的一点就是考虑边界值的问题。

但只要处理好了边界值的问题,背包类问题就基本上是一个模子的了,因此,求解价值之和最大的背包问题时,边界值应尽量定义成-INF(负无穷,可根据题目自定义),而求解价值之和最大的背包问题时，边界值尽量定义成INF（正无穷）。

3、算法源码

#include<bits/stdc++.h>
#define INF 1e9
using namespace std;
int n,x,y;
int base;//初始背包重量(初始时为使每个骨牌上端点数大于下端点数共翻转的骨牌数) 
int volumn;//初始背包体积(所有骨牌的上下差值之和,即可能变化的最大差值) 
int v[1001];//每个物品的体积(每个骨牌翻转前后变化的差值) 
int w[1001];//每个物品的重量(每个骨牌,是否翻转的状态,已翻转记为-1,未翻转记为1) 
int dp[1001][5005];//dp[i][j]表示将前i个物品放入容量为j的背包的最小重量
//若有两个多米诺骨牌分别为 a c
//                         b d
//其中a>b,c>d,则若c,d交换,则变化值为[(a-b)+(c-d)]-[(a-b)+(d-c)]=2*(c-d) 
int main(){
	cin >> n;
	for(int i = 1; i <= n; i++){
	cin >> x >> y;
	if(x > y){
		v[i] = 2*(x - y);
		volumn += (x - y);
		w[i] = 1;
	}
	else if(x < y){
		v[i] = 2*(y - x); 
		volumn += (y - x);
		w[i] = -1;
		base++;
	}
   }
	
	for(int i = 1; i <= volumn; i++)
	dp[0][i] = INF; 
	
	for(int i = 1; i <= n; i++){
		for(int j = 1; j <= volumn; j++){
			if(j < v[i])
			dp[i][j] = dp[i-1][j];
			else if(j >= v[i]){
				if(dp[i-1][j-v[i]] != INF)
				dp[i][j] = min(dp[i-1][j],dp[i-1][j-v[i]] + w[i]);
				else dp[i][j] = dp[i-1][j];
			}
			} 
		}
	int p = volumn;
    for(int i = volumn; i >= 1; i--)
    if(dp[n][i] != INF){
    	p = i;
    	break;
	}
	cout << base + dp[n][p]; 
} 

背包类问题一般都可以降成一维的,但二维的好理解一些,我这个代码就是用二维写的，除此之外，还需要注重的两处细节为:

1、边界值的处理。因为我初始化了第0行,第1~volumn列全为INF,所以根据这一行这几列推出的状态，需要进行特判。

	else if(j >= v[i]){
				if(dp[i-1][j-v[i]] != INF)
				dp[i][j] = min(dp[i-1][j],dp[i-1][j-v[i]] + w[i]);
				else dp[i][j] = dp[i-1][j];
			}

2、最大体积的找寻。因为一般的背包问题都是装满体积V,而这道题可能装不满体积V,所以需要从V开始倒着找最大的体积,除此之外,最后的背包容量一定要加上背包的初始容量。

int p = volumn;
    for(int i = volumn; i >= 1; i--)
    if(dp[n][i] != INF){
    	p = i;
    	break;
	}
	cout << base + dp[n][p];