DETR二分图匹配

DETR基于集合的目标函数，也正是因为有目标函数，所以我们才可以进行一对一的出框方式，才可以不需要NMS。

DETR最后模型的输出是一个固定的集合。无论图片是什么，我们最后都会输出N个输出。在论文里，任何一个图片进来，最后都会有N=100个输出框。这对于一般的图片来讲，框数是远多于真实的。例如，COCO数据集中一张图片里包含的最大物体数也没有超过100。所以，设置为100对于论文中是完全够用的。

问题便是：DETR每次都会输出100个，但是，一张图片的ground truth的bounding box可能只有几个。我们如何进行匹配？如何计算loss？如何知道哪个预测框对应ground truth框呢？在此，作者便把这个问题转换成了一个二分图匹配问题。

二分图匹配到底是个什么问题呢？

我们看百度或者维基百科，大多都是举得这样一个例子，如何使用一些工人去干一些活儿？从而让我们的支出是最小的。

例如我们有三个工人abc，我们需要完成三个工作xyz，因为每个工人有各自的长处短处，所以，完成工作所需要的时间和工钱也不一样。

那列出的矩阵里就可以填写每个工人完成每个任务所需要的时间或者完成任务所需要的钱数，这个矩阵叫做Cost Matrix（损失矩阵）。Cost Matrix不要求必须是正方形。

最优二分图匹配的意思，便是最后我们可以找到一个唯一解，每个人都可以分配到他最擅长的那项工作。然后使得这三个工作完成，使用的价钱最低。

其实，我们使用遍历的算法也可以将这项工作做出来。但是这样的话，成本较高。

所以有很多算法对此进行改进。其中，匈牙利算法是比较有名且高效的。

现在，一般遇到这种问题，大家会使用Scipy包里提供的一个函数，叫做Linear sum assignment去完成。

Linear sum assignment的输入便是Cost Matrix。我们只需要将Cost Matrix输入进去便可以得到一个最优序列。

DETR这篇论文使用的也正是这个函数。

我们可以把abc看作这100个预测框，将xyz看作是ground truth框，以此，我们可以得到一个最有匹配。

我们知道了可以使用这方法来解决问题，那我们矩阵里的值应该填什么呢？即损失loss。对于一般的目标检测来说，我们可以使用以下损失公式进行计算。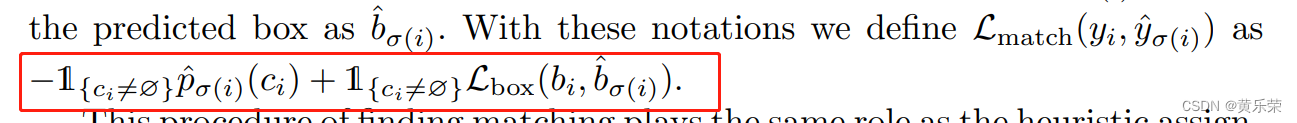

 其包含两部分，一个是分类损失，一个是框的准确率损失。

即遍历所有预测框，将预测框和所有真实框计算loss，然后将loss放入cost matrix，有了loss，我们便可以使用Linear sum assignment（匈牙利算法）得到最优解。

我们知道这100个框中哪几个框和ground truth框是对应的，接下来，我们可以算真正的目标函数，然后用这个loss做梯度回传。来更新我们的参数。

最后目标函数是：