有不足之处,还请大家私信交流。
- 版权声明:本文为自创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。(该文与课程报告相关,转载请务必附上出处),非常感谢。
- 本文链接:https://blog.csdn.net/weixin_43748432/article/details/102620916?spm=1001.2014.3001.5501
社会消费品零售总额预测
本次分析主要是基于《统计学案例与分析》中4.2节的案例数据进行分析,其主要是关于社会消费品零售总额的预测问题。数据来源于国家统计局公布的2002-2007年的月度数据,题目要求根据这些数据,运用适当的预测方法,预测2008年各月份的社会消费品零售总额。
对于这个问题,我将从以下方面入手:
- 序列的平稳性检验和纯随机性检验。即绘制时序图或自相关图进行检验。
- 根据序列的变化趋势,建立相应的模型并进行预测。
- 对比不同模型的预测均方根误差,选出最优模型。
本文使用的数据分析软件主要是SPSS21.0和excel。但对于时间序列问题来说,建议使用Eviews软件进行分析,由于时间有限,我只用了SPSS进行分析。
由于该书所提供的是2002年—2007年的数据,数据较少,有历史局限性,对得到的结果可以不具有很好的代表性。所以我又重新选取了2000年—2018年19年的数据进行建模,预测2019年各月份的数据,观察所得到的结果是否符合实际,判断其拟合效果的好坏。
社会消费品零售总额: 指批发和零售业、餐饮业、新闻出版业、邮政业和其他服务业等,售予城乡居民用于生活消费的商品和社会集团用于公共消费的商品之总量。它包括: 批发和零售业企业(单位)售予城乡居民用于生活消费和社会集团用于公共消费的商品;餐饮业出售的主食、菜肴、烟酒饮料和其他商品;新闻出版业、邮政业售予城乡居民、企事业单位、军队和武警等机构的书报杂志、音像制品、邮品等;其他服务业出售的食品、烟酒饮料、服装鞋帽、日常生活用品、医药保健用品、艺术品、工艺美术品、玩具以及其他消费品。
研究意义:各年度的社会消费品零售总额不仅反映了一个社会当期的消费水平,也能反映出消费的成长潜力和趋势,进而反映出对经济的拉动程度,因而成为制定宏观经济政策的一个重要参考指标。合理预测未来的社会消费品零售总额,对未来政策的制定具有极其重要的参考价值。
1 预备知识
1.1平稳性检验
要对时间序列进行预测,其前提是要确实时间序列数据之间是否存在相关关系,通过这种关系,我们才可以根据现在和过去的数据来预测未来的变化。
判断某序列是否平稳的方法有:
-
根据时序图和自相关图显示的特征做出判断;
时序图的数据若分布在某个常数附近上下随机波动,且波动范围有界,无明显趋势及周期特征,则为平稳序列;若有明显的趋势性或周期性,则不为平稳序列。自相关图中,一个坐标轴表示延迟时期数,一个坐标轴表示自相关系数,若自相关系数 p k p_k pk随着延迟期数k的增加而很快的衰减至0 ,则表示为平稳序列;若衰减速度太慢,则不平稳。
如下列时序图:(例子来源于《应用时间序列分析》)

从上面的时序图可以看出,北京市的最高气温始终围绕在37°附近随机波动,没有明显的趋势和周期,基本可以视为平稳序列。当然这个数据量不足以代表现在的一些实际情况,可能现在随全球变暖的趋势,每年的最高气温会有所上涨。

北京市最高气温序列自相关图如上所示,从上面的自相关图可以看出,自相关系数一直相对较小,且始终控制在2倍标准差范围内,且较快的衰减至0,也可认为该序列始终都在零轴附近波动,这明显属于平稳序列。

从该时序图可以看出,每头奶牛的月产奶量随时间逐年增长且呈现以年为周期的非平稳时间序列。

从上面的自相关图可以看出,自相关系数长期位于零轴一边,这是序列呈现单调趋势的明显特征;且其还呈现明显的正弦波动规律,这是序列具有周期性的特征。该序列是带长期递增趋势的具有周期性的时间序列图。
1.2 纯随机性检验
当一个观察完一个序列的平稳性之后,我们还需要对序列进行纯随机性检验。
- 原因是:如果序列值彼此之间没有任何相关性,则意味着该序列是一个没有记忆的序列,过去的行为对将来的发展不会造成丝毫的影响,则称这种序列为纯随机序列(也称白噪声序列),若用这种序列进行预测就没有意义了。
1.2.1定义:
对于一个时间序列
X
t
{X_t}
Xt满足如下性质:
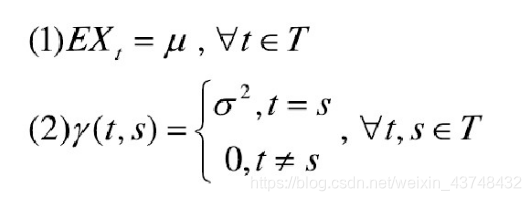
称为纯随机序列(白噪声序列)。
用R软件随机产生1000个服从标准正态分布的白噪声序列观察值,并绘制时序图。
代码和结果如下:
data1=rnorm(1000,0,1)
data1
plot(data1,type='l',xlab = 'time')

该数据始终围绕在零均值附近随机上下波动,为标准的正态白噪声序列。
1.2.2 性质
- (1)纯随机性
指白噪声序列的各项之间没有任何相关关系,也指“没有记忆”的序列。
该序列是完全无序的随机波动,没有任何值得提取的有用的相关信息,这时自协方差和自相关系数都为0,即:
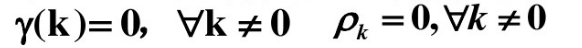
注:对于一个观察值序列,一旦相关信息提取完毕,则剩余的残差序列为纯随机性质,所以纯随机性还是判断相关信息提取是否充分的一个判别标准。 - (2)方差齐性
指白噪声序列中每个变量的方差都相等,

且根据马尔科夫定理,只有方差齐性的序列,用最小二乘法得到的未知参数估计值才是最准确,最有效的。
1.2.3 纯随机性检验
判定一个序列是否为纯随机序列,则看它是否满足纯随机性的定义和性质,即:

如果满足以上条件,则为纯随机序列。
但,现实中,一般自相关系数是很难严格等于0的,其从数学角度讲,都会有所偏差。所以需要从统计性质方面出发,来判断序列的纯随机性。

所以可提出假设条件如下:
-
原假设:延迟期数小于或等于m期的序列值之间相互独立。
备择假设:延迟期数小于或等于m期的序列值之间有相关性。 -
H 0 : ρ 1 = ρ 2 = . . . = ρ m = 0 , ∀ m ⩾ 1 H_0:\rho _1=\rho _2=...=\rho _m=0,\forall m\geqslant1 H0:ρ1=ρ2=...=ρm=0,∀m⩾1
H 1 H_1 H1:至少存在某个 ρ k ≠ 0 , ∀ m ⩾ 1 , k ⩽ m \rho _k\neq 0,\forall m\geqslant1,k\leqslant m ρk=0,∀m⩾1,k⩽m -
引入检验统计量

对刚刚所作出的标准白噪声序列计算延迟6期,12期的 Q L B Q_{LB} QLB统计量,判断该序列的随机性,( α = 0.05 \alpha =0.05 α=0.05) -
代码及结果如下:
Box.test(data1,type = c("Ljung-Box"),lag=6)
Box.test(data1,type = c("Ljung-Box"),lag=12)

从结果可以看出,该p值显著大于0.05,不能拒绝原假设,即该序列中数据之间无任何关系,没有后序分析的必要。
- ①一个平稳序列短期延迟的的序列值之间无显著相关性,则长期延迟 一般也不存在相关性。
②一个平稳序列存在短期相关性,则该序列一定不是白噪声序列。
2、案例分析
2.1 数据的预处理

上表是该案例所给的相关数据,为便于后续的分析,需要在excel中对该数据按列展示每年的消费品总额数据。
-
(1)平稳性检验

从上面的时序图可以看出,社会消费品零售总额的时序图明显为不平稳序列,其中既包含趋势上升的成分,也有明显的季节成分,且其季节周期为12(月度数据),这也比较符合经济实际。且从上图还可以看出其季节波动的振幅随着序列水平的变化而变化,则可认为该季节效应不独立,可以考虑采用乘法模型进行相应的预测建模。
Y t = T t × S t × I t Y_t=T_t×S_t×I_t Yt=Tt×St×It -
(2)纯随机性检验
引入LB统计量,检验序列的纯随机性,可以得到该检验值的P值均小于0.05,拒绝原假设,即该序列不平稳,且含有多种相关关系。因此,综合上述分析,可以考虑选择传统的分解预测方法,也可以考虑使用Holt指数平滑模型,或者ARIMA模型进行预测。在此我将用这三种方法建立模型,并对所得到的结果进行对比,判断哪种模型更为合适。
2.2 模型一:分解预测模型
由于该数据存在趋势和季节成分,一般还含有随机成分,对于课本中所给的数据来说,年份较短,周期性暂时还不能完全得到(多年的数据)。所以以下分析主要考虑趋势、季节和随机成分。
步骤如下:
- (1)确定并分离季节成分。计算季节指数,以确定时间序列中的季节成分。然后将季节成分从时间序列中分离出去,即用每一个时间序列的观测值初一相应的季节指数,消除季节性。
(2)建立预测模型并进行预测。对消除了季节影响的时间序列建立适当的预测模型,并计算预测值。
(3)计算最后的预测值。即用预测值乘以相应的季节指数,得到最终的预测值。
季节指数是衡量一个年度各月或季度的典型季节特征。一般大于1的指数对应的季节为旺季, 小于1的为淡季。
1、计算季节成分
季节指数的计算方式:移动平均趋势剔除法
步骤如下:
(1)计算12项移动平均值,并进行中心化处理。
(2)计算观察值序列与相应的中心化移动平均值的比值,再计算各比值的月份的平均值。
(3)季节指数调整。若各季节指数的平均数不等于1,则需进行调整;用每个季节比率的平均值除以他们的总平均值。
excel中部分计算过程及结果如下:


画出季节变动图如下所示:

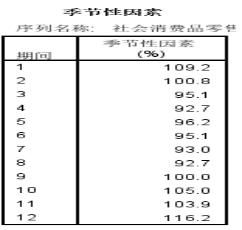
- 显然,从上图可以看出,中国社会消费品零售总额序列具有显著的季节变动特征,每年春夏季节3—8月是淡季(5,6月稍有回弹),冬季是销售旺季。
- 另外,在spss中计算季节指数,得到以下结果:(与excel计算的结果有一定的出入)。在spss中分析含有季节周期性的时间序列数据,需要先进行日期创建(数据—定义日期)。

分析—预测——季节性分解


2、分离季节成分并建模预测
第一步计算完季节指数后,需要将其分离出来,即将实际的观察值分别除以相应的季节指数,通用公式表示为:
Y t S t = T t × S t × I t S t = T t × I t \frac{Y_t}{S_t}=\frac{T_t×S_t×I_t}{S_t}=T_t×I_t StYt=StTt×St×It=Tt×It
结果可如下:
经过季节性分解之后,该序列已经不在含有季节成分,且从上图还可以看出,其社会零售总额有明显的线性趋势。因此,可以用一元线性回归模型预测各月份的社会零售总额。
在SPSS中进行线性回归,得到以下结果:

Y ^ = 2652.428 + 67.97998 t ( t = 1 , 2 , 3 , . . . , 72 ) \hat{Y}=2652.428+67.97998t (t=1,2,3,...,72) Y^=2652.428+67.97998t(t=1,2,3,...,72)
且其每月的预测数值及误差值可从表格观察得知。
3、计算最后的预测值
利用上面的回归预测值乘以相应的季节指数,可得到最终的预测值。即:
Y
t
^
=
Y
^
×
S
t
\hat{Y_t}=\hat{Y}×S_t
Yt^=Y^×St

则根据此种形式,我们可以预测出2008年各月份的数据,最终预测值如下表所示:

且可绘制最终的预测值与实际观测值的对比走势图如下:

从上图可以看出,预测效果非常显著。
可计算出其均方根误差值为:242.24。
2.3 模型二:指数平滑法模型
由于本文的数据中既含有趋势成分,还含有季节成分,所以需要构造Holt-Winters三参数指数平滑模型。其计算公式如下所示:
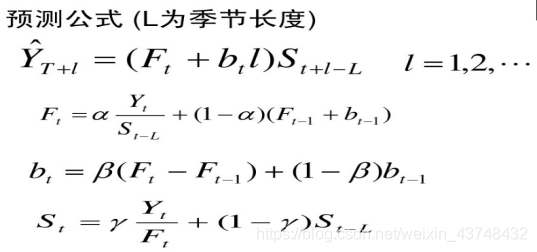
其中:Ft为t期的预测值,bt为该序列的趋势部分,St为该序列的季节因子部分,L=12。

得到最终的预测值和趋势拟合图如下:




从上图可以看出,该模型拟合的效果也相对较好,其预测均方根误差为:114.42,比分解预测的模型稍好一些。
2.3 模型三:ARIMA模型预测
2.3.1 原理
- ARIMA模型又称求和自回归移动平均模型,其是由AR模型和MA模型经过差分将序列变得平稳后得到的。所谓差分,就是指每一个观测值减去其前面的一个观测值,即 X t − X t − 1 X_t-X_{t-1} Xt−Xt−1。其中I就是指加入的整合项或差分项;d表示差分的阶数;p为自回归AR的项数;q为移动平均MA的项数。
- 由于ARIMA模型要求序列是平稳的,对于包含季节成分的非平稳序列,在使用ARMA模型预测时,需要将季节因素予以消除。
- 消除季节因素的具体办法是采用季节差分使其平稳化,季节差分是用季节周期的长度S作为滞后期的长度,对于季度数据,一阶季节差分的S=4,月份数据S=12。
- 如果季节差分后序列是平稳的,这时使用的模型表示为
A
R
I
M
A
(
p
,
d
,
q
)
(
P
,
D
,
Q
)
s
ARIMA(p,d,q)(P,D,Q)^s
ARIMA(p,d,q)(P,D,Q)s。即结合之前的分析,需要构建此类乘法模型。这里的(p,d,q)表示非季节部分;(P, D, Q)表示季节部分,即季节自回归和季节移动平均部分,S为季节周期的长度。

一般不是做研究等方面的报告,对于乘积季节模型可以直接用 A R I M A ( p , d , q ) ( P , D , Q ) s ARIMA(p,d,q)(P,D,Q)^s ARIMA(p,d,q)(P,D,Q)s来表示。
2.3.2 建模步骤
模型识别的步骤大体如下:
- 第1步:将序列平稳化。 经过d和D阶差分后,序列的自相关函数 r k r_k rk在k增大时迅速衰减并趋于0,这时d和D的差分阶数就是d和D的取值。
- 第2步:识别模型的阶数。 对于平稳的原始序列(或差分平稳的序列)的偏自相关函数有p个显著不为0的峰值,也就是在p个值后截尾,它的自回归阶数就是p;如果自相关函数有q个显著不为0的峰值,也就是在q个值后截尾,它的移动平均阶数就是q。如果季节偏自相关函数有P个显著不为0的峰值,季节自回归的阶数就是P;如果季节自相关函数有Q个显著不为0的峰值,季节移动平均的阶数就是Q。
即如下表所示,具体的判别方法后面会根据数据所得到的图表进行分析:
| ACF | Q、q |
|---|---|
| PACF | p、P |
注:
p:出去季节性变化之后的序列所滞后的p期,通常为0或1,大于1的情况很少;
d:除去季节性变化之后的序列进行d阶差分,通常取值为0,1或2;
q:除去季节性变化之后的序列进行q次移动平均,通常取值0或1,很少会超过2;
P,D,Q分别表示包含季节性变化的序列所做的事情。
- 第3步:模型诊断。 诊断所选择的模型是否正确,其方法通常是考察残差序列的自相关图。如果所选择的模型是正确的,那么利用该模型预测产生的误差应该是白噪声序列,此时,残差序列的自相关图没有固定模式。
具体步骤如下所示:
为判断社会消费品零售总额序列的平稳性,(其时序图在之前已经给出)。
- 1、首先绘制出原始序列的自相关图和偏自相关图。社会消费品零售总额自相关图和偏自相关图如下所示。
在SPSS中:分析—预测—自相关

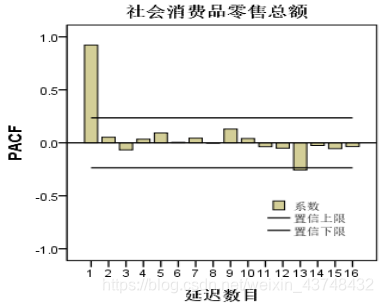
从上面的序列自相关图和偏自相关图可以看出,与之前分析的时序图结果一致,其自相关函数没有快速的收敛到0,严重拖尾,具有明显的趋势特征,且偏自相关系数有明显的峰值,序列不平稳,需要将序列平稳化,即对序列先进行1阶差分。 - 2、差分使序列平稳化,并确定相应的阶数
- 将序列1阶差分

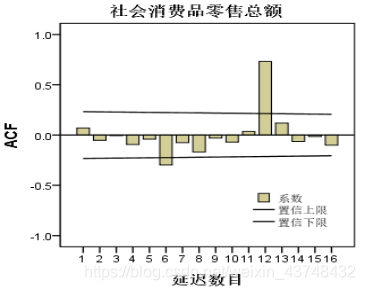

从上面的图可以看出,该序列的趋势特征已基本消除,序列已经平稳。此时,可以确定d=1,即差分的阶数。且其自相关图和偏自相关图都含有一个明显的峰值,可以直接确定p=1,q=1。
其自相关图在k=12的滞后期数处,有明显的峰值,说明该序列存在典型的季节成分。需要进行季节差分。差分的滞后期长度为S=12(月度)。 - 季节差分




从上面的自相关表可以看出,所有P值都大于0.05,满足白噪声检验,说明季节差分后的序列已经平稳化,且不再含有其他未提取的信息。
且可确定季节差分的阶数D=1;且其自相关图相对含有两个明显的峰值,则Q=2;偏自相关图含有一个明显的峰值,P=1。
所以可以确定最终的模型为:ARIMA(1,1,1)(1,1,2)12。 - 3、模型拟合

可以得到相应的拟合结果如下:
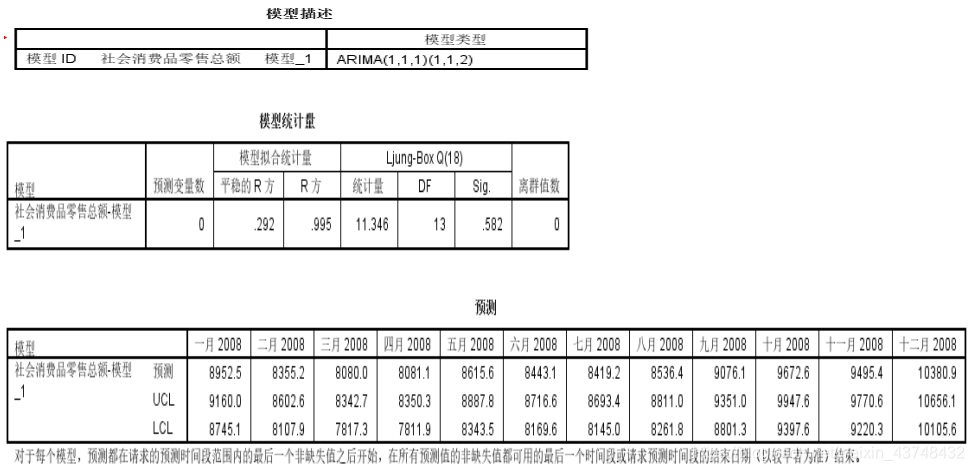
从上面的图中,我们可以看出,该模型的拟合效果非常好,R方达到了99.5%左右。

从拟合的趋势线来看,也可以得出其拟合的效果很好。 - 4、模型诊断
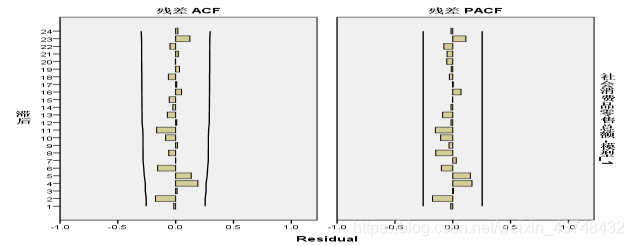
且从上面的残差序列的自相关图和偏自相关图来看,都是随机分布在0点附近,无任何规律性,可说明其满足白噪声检验,其结果拟合效果很好。
3、模型比较
对上述三个模型的预测结果进行比较,可以得到最优的预测模型。

从其均方根误差来看,季节ARIMA(1,1,1)(1,1,2)12优于其他两个模型,对于类似此类问题, 即既含有趋势又含有季节成分的序列来说,可以此种模型进行建模,可以达到较好的预测效果。

从上面的预测趋势线直观上看不出有多大的差异,但是从均方根误差来看还是有比较大的误差。
4、2000-2019年社会消费品总额预测分析
从国家统计局网站获取相应的数据如下:

4.1 数据处理
由于国家统计局中2012年之后社会消费品总额的统计方法有所改变,只提供1-2月的总的消费品总额数据,需要进行相应的数据缺失处理。在spss中采用专家建模法,用预测曲线来拟合相应的缺失值数据,拟合效果达到99%以上,再根据2个月的总额差值,平分到每个月中,可能会造成相应的偏差。得到完整的数据。

4.2 平稳性检验与纯随机性检验
1、绘制时序图

从上面的时序图来看,很明显可以看出,其序列不平稳,其而含有明显的趋势和季节成分。
2、纯随机性检验
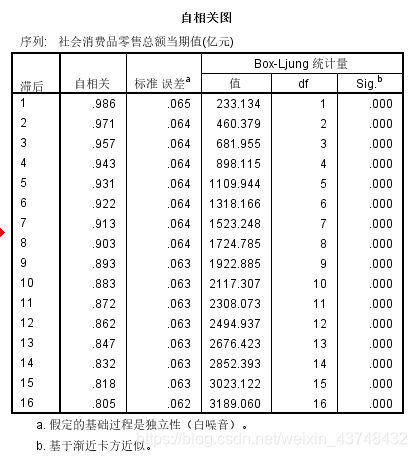
p值都小于0.05,不满足白噪声序列的检验。

从其自相关图和偏自相关图来看,也不满足平稳性的条件。
4.3 建立预测模型
在此不考虑其分解预测的模型。
- 在spss中分析—预测—创建模型
- 利用专家建模器建模,其可以自动对非平稳序列进行平稳化,运用指数平滑法和ARIMA模型进行预测,并最终显示拟合最优的模型结果。

结果如下所示:

专家判别,所拟合的模型为 A R I M A ( 0 , 1 , 1 ) ( 1 , 1 , 0 ) 12 ARIMA(0,1,1)(1,1,0)12 ARIMA(0,1,1)(1,1,0)12

模型的拟合优度达到了99.9%左右,拟合效果非常好。

且其残差值序列的自相关系数和偏自相关系数都在2倍标准差以内,满足白噪声序列的条件。

5 python分析
5.1 Python时间序列分析相关原理
(1)Python版本及相应的编译环境
本次编程环境下主要在python3.7下进行,在pycharm2019社区版编辑器中编写相应的代码。其中还集成了anaconda中的一些标准库或第三方库等。
(2)时间序列分析所需第三方库
本次所进行的时间序列分析总共需要用到下面这些第三方库或标准库:warnings,itertools,itertools ,numpy,pandas(数据分析库),csv,matplotlib(绘图库)和statsmodels(时间分析处理)库。
在程序开头,需要导入这些库名:如import matplotlib.pyplot as plt等。
(3)所涉及的时间序列分析的相关指标

③ADF检验:又称单位根检验。如果序列平稳,则不存在单位根,否则就会存在单位根。若数据不平稳,则可以做差分变换,查看差分后是否平稳。
ADF原假设为:序列存在单位根,即序列为非平稳序列;对于一个平稳的时序数据,就需要在给定的置信水平上满足显著性条件,即p值小于置信水平,此时拒绝原假设,序列为平稳序列。
若得到的统计量显著小于3个置信度(1%,5%,10%)的临界统计值时,说明是拒绝原假设的。另外是看P-value是否非常接近0。(4位小数基本即可)
(4)模型选择的判别准则
在模型选择的时候,对于模型的参数估计问题均采用似然函数作为目标函数,当训练数据足够多时,可以不断提高模型精度,但是以提高模型复杂度为代价的,同时也会带来一个非常普遍的问题——过拟合。所以,模型选择问题在模型复杂度与模型对数据集描述能力(即似然函数)之间需要找寻一个最佳的平衡。
在此案例中主要介绍两种选择方法——赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则(Bayesian Information Criterion,BIC)。
①AIC准则:是衡量统计模型拟合优良性的一种标准,由日本统计学家赤池弘次在1974年提出,它建立在熵的概念上,提供了权衡估计模型复杂度和拟合数据优良性的标准。其公式定义如下所示:

其中k是模型参数个数,L是似然函数。从一组可供选择的模型中选择最佳模型时,通常选择AIC最小的模型。当模型之间存在较大差异时,差异主要体现在似然函数项,当似然函数差异不显著时,上式第一项,即模型复杂度则起作用,从而参数个数少的模型是较好的选择。
一般而言,当模型复杂度提高(k增大)时,似然函数L也会增大,从而使AIC变小,但是k过大时,似然函数增速减缓,导致AIC增大,模型过于复杂容易造成过拟合现象。所以当要选取AIC最小的模型时,AIC不仅要提高模型拟合度(极大似然),就需要引入惩罚项,使模型参数尽可能少,这有助于降低过拟合的可能性。
②BIC准则:1978年由Schwarz提出。当训练模型时,增加参数数量,也就是增加模型复杂度,会增大似然函数,但是也会导致过拟合现象,针对该问题,BIC也引入了与模型参数个数相关的惩罚项,BIC的惩罚项比AIC的大,考虑了样本数量,样本数量过多时,可有效防止模型精度过高造成的模型复杂度过高的问题。用公式表示如下所示:

其中,k为模型参数个数,n为样本数量,L为似然函数。kln(n)惩罚项在维数过大且训练样本数据相对较少的情况下,可以有效避免出现维度灾难现象。
在模型选择时,都是选择使两个准则最小的对应模型。
5.2实际操作
在python程序中,总共分为以下七个部分:
(1)首先是导入相关库名和所需数据:如:import statsmodels.api as sm
data_files = csv.reader(open(‘yuce2019.csv’,‘r’))
(2)①用pandas和matplotlib库绘制原始数据的时序图
df = pd.DataFrame(dataSet,index=dateSet,columns=[‘real value’])
所绘制的时间序列图与SPSS中绘制的结果大致相同。

②将序列均值化并进行一阶差分,检验差分后的ADF值,判断序列的平稳性。df_kill_mean_1 = df_kill_mean.diff(1).dropna() #对序列1阶差分

从序列图可以看出,均值化后在进行1阶差分的序列是不平稳的。
ADF检验值为:(-1.6607210413504088, 0.4514552596360234, 13, 222, {‘1%’: -3.460154163751041, ‘5%’: -2.874648939216792, ‘10%’: -2.5737567259151044}, 3151.985392670633)。从结果可以看出P值为0.45大于置信水平,不能拒绝原假设,即序列不平稳。
(3)分解建模,确定模型参数,即绘制ACF和PACF图。
①绘制ACF和PACF图
#绘制自相关图
plot_acf(df_kill_mean_1,lags=24).show() # 其中lags参数是指横坐标最大取值
#绘制偏相关图
plot_pacf(df_kill_mean_1,lags=24).show()
结果如下所示:

从两个图形来看,都呈现拖尾的现象,且每隔12个月份会出现明显的峰值,该序列明显含有季节因素,序列不平稳。
我们可以通过分解的方式将时序数据分离成不同的成分,它主要将时序数据分离为Trend(成长趋势)、seasonal(季节性趋势)、Residuals(随机成分)。然后我们分别对这三个分离的序列进行ARIMA建模得到较好的模型,最后再将模型相乘便可以得到最后的ARIMA模型。
decomposition = seasonal_decompose(df_kill_mean_1, freq=12)
trend = decomposition.trend # 趋势部分
seasonal = decomposition.seasonal # 季节性部分
residual = decomposition.resid # 随机部分
得到如下图形:
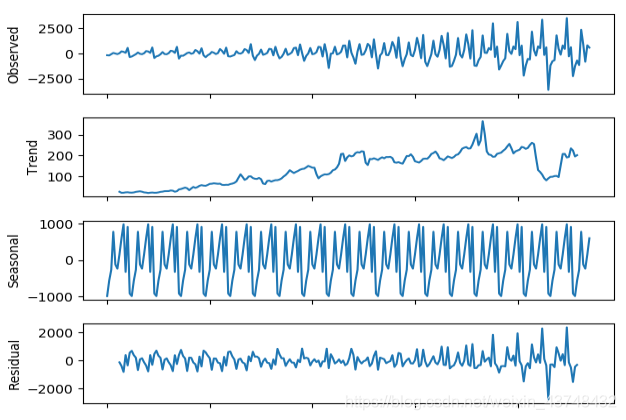
从上述图形中也明显可以看出,序列由一种明显的上升趋势,且存在明显的季节性因素。
②确定参数
由于上述图形不能尽快确定模型的参数值,我们接着引入季节ARIMA模型对序列进行拟合。
(4) ARIMA时间序列模型的参数选择
①使用“网格搜索”来迭代地探索参数的不同组合。即使用statsmodels模块的SARIMAX()函数拟合一个新的季节性ARIMA模型,并评估其整体质量。
seasonal_pdq = [(x[0], x[1], x[2], 12) for x in list(itertools.product(p, d, q))]
②引入AIC判别准则,选取最小的模型
print(‘ARIMA{}x{} - AIC:{}’.format(param, param_seasonal, results.aic))
得到部分结果如下所示:
ARIMA(0, 1, 0)x(0, 1, 0, 12) -AIC:3401.083246271593
ARIMA(0, 1, 0)x(0, 1, 1, 12) - AIC:3222.9120035730584
ARIMA(0, 1, 1)x(1, 1, 0, 12) - AIC:3054.0059015131374
…
ARIMA(0, 1, 1)x(0, 1, 1, 12) - AIC:3027.6415321321565
ARIMA(0, 1, 1)x(1, 1, 1, 12) - AIC:3027.774444326872
ARIMA(1, 1, 0)x(0, 1, 1, 12) - AIC:3163.799545880843
ARIMA(1, 1, 0)x(1, 1, 0, 12) - AIC:3162.729511047489
ARIMA(1, 1, 0)x(1, 1, 1, 12) - AIC:3164.353850738278
ARIMA(1, 1, 1)x(0, 1, 1, 12) - AIC:3019.1824357360438
ARIMA(1, 1, 1)x(1, 1, 1, 12) - AIC:3018.546787777849
从上述结果中可以得出,模型ARIMA(1, 1, 1)x(1, 1, 1) 12的AIC是最小的,由此判定该模型为最佳模型。
(5)得到最佳模型的特征参数
将上一步所得到的模型参数代入,得到具体的模型指标值。
mod = sm.tsa.statespace.SARIMAX(df,order=(1,1,1),seasonal_order=(1, 1, 1,12),
enforce_stationarity=False,enforce_invertibility=False)
得到下面的结果:

从上面的系数表输出结果可以得到大量的信息,coef列显示每个特征的重量(即重要性)以及每个特征如何影响时间序列。 P>|z| 列通知我们每个特征重量的意义。 这里,每个重量的p值都低于或接近0.05 ,所以在我们的模型中保留所有权重是合理的。
(6)模型诊断
主要确保我们的模型中的残差是不相关的,并且平均分布为零。 如果季节性ARIMA模型不能满足这些特性,那模型就需要进一步改进。
result.plot_diagnostics(figsize=(15, 12)) #模型诊断
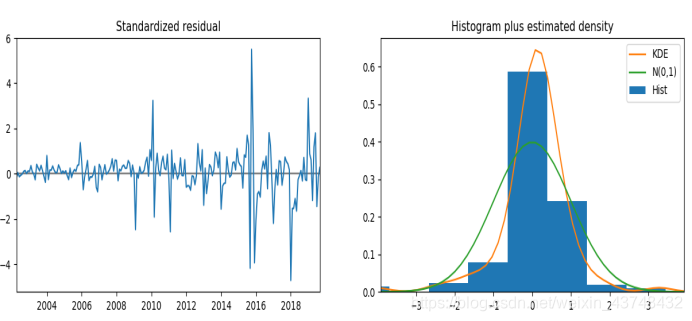

随着时间的推移(左上图)的残差不会显示任何明显的季节性,大致可以判定该序列为白噪声序列。 也可通过右下角的自相关来证实,基本都在0附近波动,这表明时间序列残差与其本身的滞后值具有低相关性。
在右上图中,可以看到红色KDE线与N(0,1)蓝色的线的对比情况,后者是标准正态分布,平均值0 ,标准偏差为1 ),从图形来看,有一定小偏差,但大致呈现正态分布的形式。
左下角的qq图显示,残差(蓝点)的有序分布遵循采用N(0, 1)的标准正态分布采样的线性趋势。 只是偶尔有部分异常点出现,可以忽略。
(7)预测及图形的绘制
pred_uc = result.get_forecast(steps=15) #预测15期的结果。即2019.09-2020.12的数据
ax.set_xlabel(‘Date’)
ax.set_ylabel(‘cunsumer goods’)
可以得到下面的结果。
2019年10-12月的社会消费品零售总额预测值为:38005.88514999,37757.53354921,38355.92553522。与SPSS所得到的结果有一些出入。将结果导入到spss中,计算其均方根误差,可以得到下面的结果。

从上述结果可以看出,ARIMA(1,1,1)(1,1,1)12稍微比ARIMA(0,1,1)(1,1,0)12模型的拟合效果要好一些。由于在python中所绘制的图形不是特别理想,将其结果导入SPSS中,绘制预测图形如下所示:

从图形来看,该模型拟合效果非常好。
5.3最终结果
对于本案例所提到的社会消费品的数据,要预测其未来的走势,经过分析,其属于时序问题,要挖掘其潜在的信息,拟合相应的季节ARIMA模型,并对后期进行预测。所拟合的ARIMA(1,1,1)(1,1,1)12具有较高的精度,可为后期的一些预测和政策制定提供相应的依据。
总结
- 从拟合趋势线来看,模型拟合效果非常好。
- 通过上面的分析和预测,我们看到各月的社会消费品零售总额当期值存在明显的季节性波动。
一年之中整体呈上升趋势,近10年来都保持着4月零售总额较低,7月小幅回落,10月迅速增长的模式。 - 每个数据波动的背后都有着复杂的社会因素,有的有规律可循,有的属于偶然突发。
- 季节性ARIMA模型的预报是基于一定规律下的预测,无法应对外生的随机干扰。对国民经济发展趋势进行分析,除了要善用模型,还要对市场发展、政策形势有足够深入的了解。



























 1296
1296

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








