离线强化学习系列3(算法篇): AWR(Advantage-Weighted Regression)算法详解与实现

论文信息：Xue Bin Peng, Aviral Kumar, Grace Zhang, Sergey Levine: “Advantage-Weighted Regression: Simple and Scalable Off-Policy Reinforcement Learning”, 2020;
xbpeng.github.io/projects/AWR/2019_AWR.pdf

本篇论文由伯克利Sergey Levine团队的Xue Bin Peng以第一作者提出，投稿到ICLR 2020和ICLR 2021，尽管都被Reject了，但是论文的观点和方法实验还是很值得学习的。

摘要：Advantage-Weighted Regression (AWR)，从名字上来看，就是Advantage版本的Reward-Weighted Regression (RWR)。AWR通过对RWR进行改进，包括两个标准的监督学习步骤，一个通过利用累积奖励的回归来训练价值函数基线，另一个通过加权回归来训练策略。核心思想是将策略优化过程看成是极大似然估计问题，在策略提升过程中，用优势函数进行权重似然估计。作者在Mujoco环境中和其他算法进行了比较，展现了算法的有效性。

1、预备知识

1.1 累计奖励

$$J(\pi )={\mathbb{E}}_{\tau \sim p_{\pi }(\tau )}\left[\sum _{t=0}^{\infty }{\gamma }^t{r}_t\right]={\mathbb{E}}_{\mathbf{s}\sim d_{\pi }(\mathbf{s}),a\sim \pi (\mathbf{a}\mid \mathbf{s})}[r(\mathbf{s},\mathbf{a})]$$
策略$\pi$的累计奖励的期望，$r(s,a)$换成$R(s,a)$更好。

1.2 RWR

$${\pi }_{k+1}=\underset{\pi }{\mathrm{argmax}}{\mathbb{E}}_{\mathbf{s}\sim d_{{\pi }_k}(\mathbf{s})}{\mathbb{E}}_{\mathbf{a}\sim {\pi }_k(\mathbf{a}\mid \mathbf{s})}\left[\log \pi (\mathbf{a}\mid \mathbf{s})\exp \left(\frac{1}{\beta }{\mathcal{R}}_{\mathbf{s},\mathbf{a}}\right)\right]$$
通过使用当前策略${\pi }_k$生成数据，新策略${\pi }_{k+1}$（使用最大似然准则下的监督学习）拟合到给定状态的动作条件分布上，加权表示后返回。

2、AWR

2.1 策略评估

策略$(\pi )$相对于策略$(\mu )$的提升用下式来表示：
$$\eta (\pi )=J(\pi )-J(\mu )$$
然后进行拟合，可以写成在策略$(\pi )$下进行采样，对$(\mu )$的优势函数计算期望
$$\eta (\pi )={\mathbb{E}}_{\mathbf{s}\sim d_{\pi }(\mathbf{s})}{\mathbb{E}}_{\mathbf{a}\sim \pi (\mathbf{a}\mid \mathbf{s})}\left[{\mathcal{R}}_{\mathrm{s},\mathbf{a}}^{\mu }-V^{\mu }(\mathbf{s})\right]$$

为求得约束条件下的最优策略，可以采用拉格朗日乘数法进行求解，约束条件是策略$\pi$和策略$\mu$尽可能相似，利用KL散度的概念进行表示：
$$\begin{array}{rl}\arg \underset{\pi }{\max }& {\int }_{\mathbf{s}}{d}_{\mu }(\mathbf{s}){\int }_{\mathbf{a}}\pi (\mathbf{a}\mid \mathbf{s})\left[{\mathcal{R}}_{\mathbf{s},\mathbf{a}}^{\mu }-V^{\mu }(\mathbf{s})\right]d\mathbf{a}d\mathbf{s}\\ & \text{ s.t. }{\int }_{\mathbf{s}}{d}_{\mu }(\mathbf{s})D_{\mathrm{K}\mathrm{L}}(\pi (\cdot \mid \mathbf{s})||\mu (\cdot \mid \mathbf{s}))d\mathbf{s}\le ϵ\end{array}$$

构建拉格朗日方程，带入化简得：
$$\mathcal{L}(\pi ,\beta )={\int }_{\mathbf{s}}{d}_{\mu }(\mathbf{s}){\int }_{\mathbf{a}}\pi (\mathbf{a}\mid \mathbf{s})\left[{\mathcal{R}}_{\mathrm{s},\mathbf{a}}^{\mu }-V^{\mu }(\mathbf{s})\right]d\mathbf{a}d\mathbf{s}+\beta \left(ϵ-{\int }_{\mathbf{s}}{d}_{\mu }(\mathbf{s}){\mathrm{D}}_{\mathrm{K}\mathrm{L}}(\pi (\cdot \mid \mathbf{s})\Vert \mu (\cdot \mid \mathbf{s}))d\mathbf{s}\right)$$

对$pi$求偏导得到的最优解是：
$${\pi }^{\ast }(\mathbf{a}\mid \mathbf{s})=\frac{1}{Z(\mathbf{s})}\mu (\mathbf{a}\mid \mathbf{s})\exp \left(\frac{1}{\beta }\left({\mathcal{R}}_{\mathrm{s},\mathbf{a}}^{\mu }-V^{\mu }(\mathbf{s})\right)\right)$$

若要将其用神经网络的形式进行表示，也就是最优策略投影到策略网络上，${\pi }^{\ast }$和${\pi }^{\ast }$的KL散度尽可能小，转换成优势函数回归的样式：

$$\begin{array}{rl}& \underset{\pi }{\mathrm{argmin}}{\mathbb{E}}_{\mathbf{s}\sim d_{\mu }(\mathbf{s})}\left[{\mathrm{D}}_{\mathrm{K}\mathrm{L}}\left({\pi }^{\ast }(\cdot \mid \mathbf{s})\Vert \pi (\cdot \mid \mathbf{s})\right)\right]\\ & =\underset{\pi }{\mathrm{argmin}}{\mathbb{E}}_{\mathrm{s}\sim d_{\mu }(\mathbf{s})}\left[{\mathrm{D}}_{\mathrm{K}\mathrm{L}}\left(\frac{1}{Z(\mathbf{s})}\mu (\mathbf{a}\mid \mathbf{s})\exp \left(\frac{1}{\beta }\left({\mathcal{R}}_{\mathrm{s},\mathbf{a}}^{\mu }-V^{\mu }(\mathbf{s})\right)\right)||\pi (\cdot \mid \mathbf{s})\right)\right]\\ & =\underset{\pi }{\mathrm{argmax}}{\mathbb{E}}_{\mathbf{s}\sim d_{\mu }(\mathbf{s})}{\mathbb{E}}_{\mathbf{a}\sim \mu (\mathbf{a}\mid \mathbf{s})}\left[\log \pi (\mathbf{a}\mid \mathbf{s})\exp \left(\frac{1}{\beta }\left({\mathcal{R}}_{\mathbf{s},\mathbf{a}}^{\mu }-V^{\mu }(\mathbf{s})\right)\right)\right]\end{array}$$

2.2 伪代码

AWR算法利用Off-policy获取的数据队列D，每次迭代包括以下步骤：

• 使用策略${\pi }_k$对一系列轨迹进行采样，将其存储在回放缓冲区$D$中，采样得到的数据以先进先出队列的形式进行储存。
• 在$D$中对数据进行采样，利用数据去拟合一个V函数。
• 使用优势加权回归在相同的缓冲区内来拟合新策略，进行策略优化，其中缓冲区中的状态动作对根据指数优势函数进行加权，并对其进行拟合。

2.3 off policy

on policy的采样效率很低，每次迭代中收集到的数据在一次更新迭代之后会被丢弃，为了充分提升样本的利用效率，算法利用了Off-policy思想，最新策略${\pi }_k$收集到的数据存储到缓冲区$D$中。对V函数进行拟合和策略改进时，采样策略为之前的策略或者其他不同策略共同组成的一个复合策略。

2.3.1 样本分布

经验池$D$是之前的策略采集的数据，轨迹分布、状态动作分布和状态分布如下：

$$\mu (\tau )=\sum _{i=1}^k{w}_i{d}_{{\pi }_i}(\tau ),\mu (\mathbf{s},\mathbf{a})=\sum _{i=1}^k{w}_i{d}_{{\pi }_i}(\mathbf{s}){\pi }_i(\mathbf{a}\mid \mathbf{s}),d_{\mu }(\mathbf{s})=\sum _{i=1}^k{w}_i{d}_{{\pi }_i}(\mathbf{s})$$

2.3.2 策略提升

添加策略权重
$$\begin{array}{rl}\eta (\pi )& =J(\pi )-J(\mu )\\ & =J(\pi )-\sum _{i=1}^k{w}_{i}J\left({\pi }_i\right)\\ & =\sum _{i=1}^k{w}_i\left(J(\pi )-J\left({\pi }_i\right)\right)\\ & =\sum _{i=1}^k{w}_i\left({\mathbb{E}}_{\mathbf{s}\sim d_{\pi }(\mathbf{s}),\mathbf{a}\sim \pi (\mathbf{a}\mid \mathbf{s})}\left[A^{{\pi }_i}(\mathbf{s},\mathbf{a})\right]\right)\end{array}$$
构建拉格朗日方程：
$$\begin{array}{rl}\mathcal{L}(\pi ,\beta ,\alpha )=& \left(\sum _i{w}_i{\mathbb{E}}_{\mathbf{s}\sim d_{{\pi }_i}(\mathbf{s})}{\mathbb{E}}_{\mathbf{a}\sim \pi (\mathbf{a}\mid \mathbf{s})}\left[{\mathcal{R}}_{\mathbf{s},\mathbf{a}}^{{\pi }_i}-V^{{\pi }_i}(\mathbf{s})\right]\right)\\ & +\beta (ϵ-{\mathbb{E}}_{\mathbf{s}\sim d_{\mu }(\mathbf{s})}{\mathrm{D}}_{\mathrm{K}\mathrm{L}}\left(\pi (\cdot \mid \mathbf{s})\Vert \frac{{\sum }_{i=1}^k{w}_i{d}_{{\pi }_i}(\mathbf{s}){\pi }_i(\cdot \mid \mathbf{s})}{{\sum }_{j=1}^k{w}_j{d}_{{\pi }_j}(\mathbf{s})}\right)\\ & +\int {\alpha }_{\mathbf{s}}\left(1-\int \pi (\mathbf{a}\mid \mathbf{s})d\mathbf{a}\right)d\mathbf{s},\end{array}$$

求解得到的结果：
$$\underset{\pi }{\mathrm{argmax}}\sum _{i=1}^k{w}_i{\mathbb{E}}_{\mathbf{s}\sim d_{{\pi }_i}(\mathbf{s})}{\mathbb{E}}_{\mathbf{a}\sim {\pi }_i(\mathbf{a}\mid \mathbf{s})}\left[\log \pi (\mathbf{a}\mid \mathbf{s})\exp \left(\frac{1}{\beta }\left({\mathcal{R}}_{\mathbf{s},\mathbf{a}}^{{\pi }_i}-\frac{{\sum }_j{w}_j{d}_{{\pi }_j}(\mathbf{s})V^{{\pi }_j}(\mathbf{s})}{{\sum }_j{w}_j{d}_{{\pi }_j}(\mathbf{s})}\right)\right)\right]$$

2.3.3 价值函数

设置baseline，在$D$中采样数据进行拟合得到价值函数：
$$\bar{V}=\underset{V}{\mathrm{argmin}}\sum _i{w}_i{\mathbb{E}}_{\mathbf{s},\sim d_{{\pi }_i}}(\mathbf{s}),\mathbf{a}\sim {\pi }_i(\mathbf{a}\mid \mathbf{s})\left[{\Vert {\mathcal{R}}_{\mathrm{s},\mathbf{a}}^{{\pi }_i}-V(\mathbf{s})\Vert }^2\right]$$

3、实验

在mujoco、Humanoid和Dog上实验

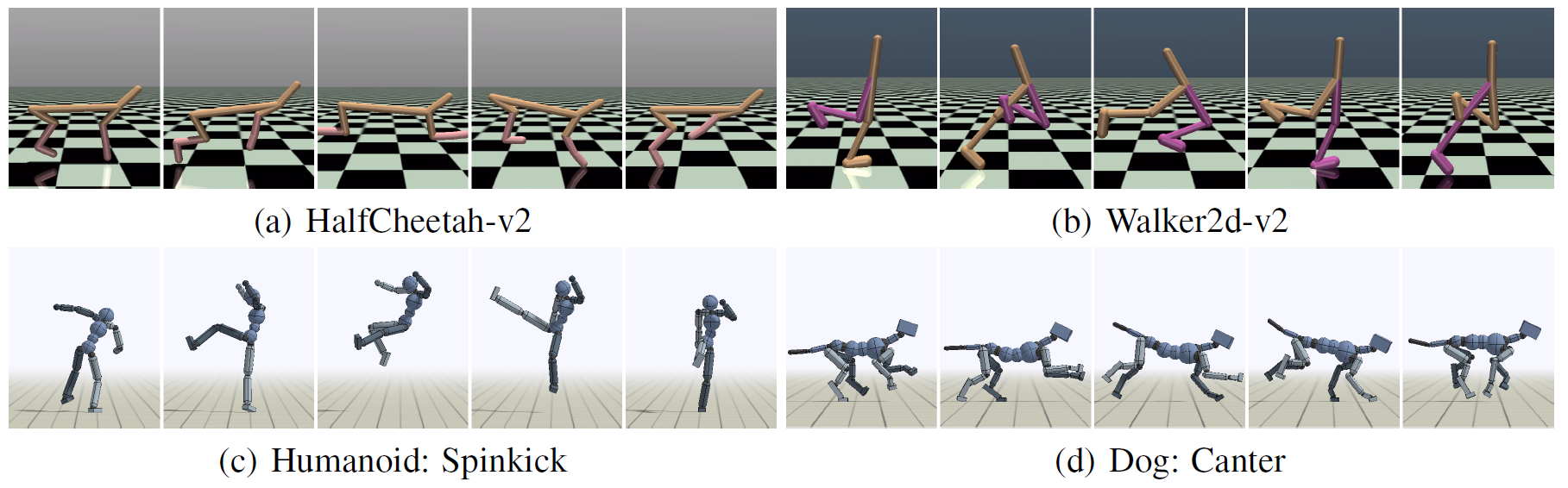
和其他算法进行比较

AWR在某些环境上表现很好

AWR相对于RWR有了明显提升

时间更短，可以更快的收敛

在静态数据集上效果也不错

Github
结构很清楚，而且比较简单

参考文献

[1]. Xue Bin Peng,Aviral Kumar,Grace Zhang,Sergey Levine: “Advantage-Weighted Regression: Simple and Scalable Off-Policy Reinforcement Learning”, 2019; xbpeng.github.io/projects/AWR/2019_AWR.pdf7.