参考:https://blog.csdn.net/qq_29180475/article/details/105779644
同名端
可以理解为从这端输入电流,两个线圈产生的磁通方向相同。根据右手定则也很好判断,两个线圈在同一条直的铁芯缠绕方式相同时,开始的两端就是同名端。

下面这个是一个环形铁芯可根据在铁芯中产生磁通方向判断。

磁通链和电流变化关系
参考:https://zhuanlan.zhihu.com/p/149830125
直流加在电感两端的电流和电压变化曲线。

电流和磁通链的关系是
ψ
L
=
N
Φ
L
=
L
⋅
i
ψ_{L}\ =\ NΦ_{L}=L\cdot i
ψL = NΦL=L⋅i
电压和磁通的关系
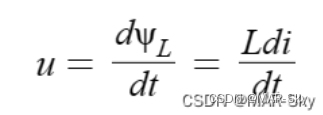
变压器两端电压电流通过磁通链变化传递关系

通过直流激励电感分析原线圈和副线圈的电流电压变化
原线圈端加直流电源后原线圈的电压电流随时间变化如下,

根据感应电压和磁通链的关系,以及磁通链和电流的关系可知副线圈的感应电压和原线圈的电流变化斜率成正比。副线圈电压变化和原线圈基本走向一致,不同的是线圈匝数导致的数值不同。

原线圈和副线圈的电压方向分析
从下图可以看出,虽然是同名端,但原线圈是电流从同名端流入而副线圈是从同名端流出。


从电源和负载方面分析
将变压器做为一个整体来看,变压器的原线圈在一次侧就是做为负载,而变压器的副线圈在二次侧做为负载的电源。所以同名端相对另一端的电压正负性是一样的。

从磁通链变化分析
当铁芯中磁通链增加,副线圈会产生阻止这种磁通链变化的电压。根据同名端定义,同时流入同名端会产生相同方向的磁通链。但这种阻止的感应电压会在原线圈增加磁通链,而副线圈会产生相反方向的磁通链,这样的电流必然是相反的。如下图,若判断同名端,则同时流入产生相同磁通链,但做为感应电流为了阻止这种磁通链变化,所以一定产生相反电流。
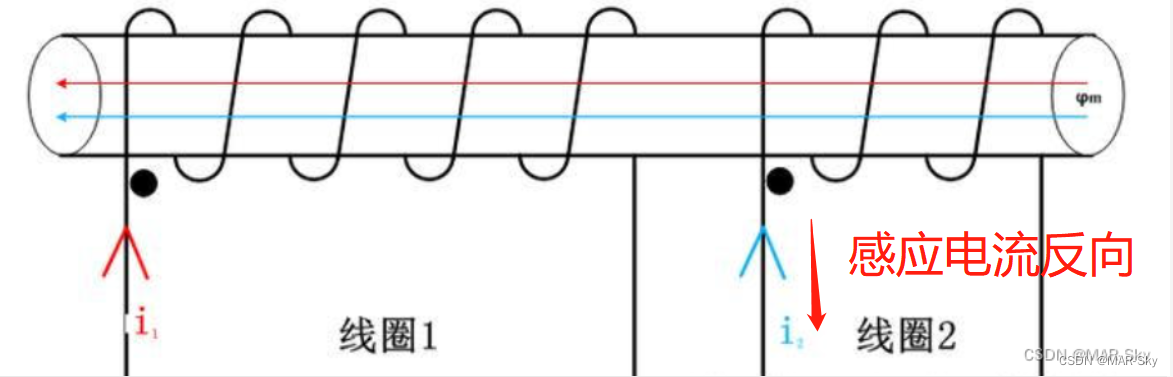
一个小实验
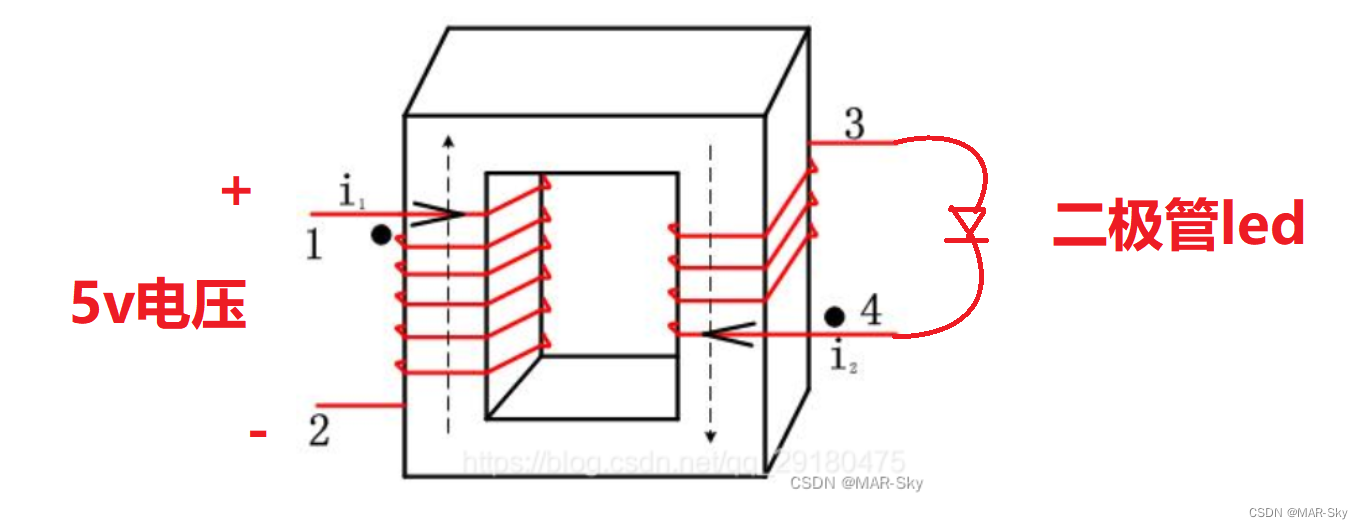
如上图,在铁芯的副线圈端连接一个二极管,注意方向。
操作步骤,(为了防止电源烧毁,尽量减少原线圈通电时间,和增加线圈匝数,一般电源有防短路功能。)
1,先接好电源一端,不要把电源两端都连接上,把二极管先连接好
2,然后把电源另一端触碰接触,并快速断开,发现断开的时候二极管闪一下
分析
同名端的电压相对于另一端电压的极性是不改变的。当左侧接入电源,导致副线圈的同名端4的电压高于3,这时由于二极管的特性不能导通,当断电后磁通链减少,副线圈产生相反电流,所以导通。
当然若这个二极管接的是反向的,那么但接接通电源时led灯会闪一下

























 2212
2212

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








