Pytorch 学习第【6】天

原创已于 2022-05-02 23:43:04 修改 · 1.5k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#pytorch #学习 #深度学习

于 2022-05-02 23:42:12 首次发布

Pytorch 专栏收录该内容

7 篇文章

订阅专栏

本文详细介绍了PyTorch中的填充层（ReflectionPad2d和ReplicationPad2d）、非线性激活（ReLU和Sigmoid）以及归一化层（BatchNorm2d和InstanceNorm2d）。通过实例代码展示了各层的使用方法，解释了参数含义和计算过程，加深了对这些关键层的理解。

1. Pytorch 学习

今天主要学习Pytorch的Padding Layers，Non-linear Activations、Normalization Layers等的内容【PS：注意结合前边内容。】
Pytorch 学习第【1】天
 Pytorch 学习第【2】天
 Pytorch 学习第【3】天
 Pytorch 学习第【4】天
 Pytorch 学习第【5】天

2. 填充层 Padding Layers

2.1 torch.nn.ReflectionPad2d 和 torch.nn.ReplicationPad2d

使用输入边界的反射来填充输入张量。
参数：

torch.nn.ReflectionPad2d(padding)
torch.nn.ReplicationPad2d(padding)

解析：
padding (int, tuple) ：填充的大小。如果是int，在所有边界使用相同的padding。如果是4元组，则使用padding_left、padding_right、padding_top、padding_bottom

2.1.1 padding 参数

（1）例子：
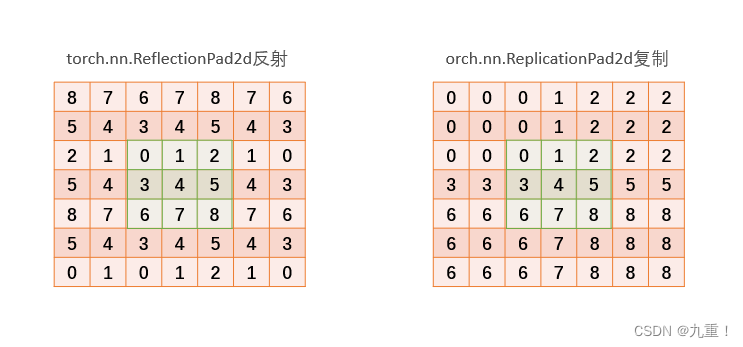
在这里插入图片描述

2.1.2 python代码例子

2.1.2.1 上边的例子复现代码

from torch import nn
import torch

jiuchong  = nn.ReflectionPad2d(2)
input = torch.arange(9, dtype=torch.float).reshape(1, 1, 3, 3)
output=jiuchong(input)
print(input)
print(output)

jiuchong2  = nn.ReplicationPad2d(2)
output2=jiuchong2(input)
print(output2)

输出结果：

ensor([[[[0., 1., 2.],
          [3., 4., 5.],
          [6., 7., 8.]]]])
tensor([[[[8., 7., 6., 7., 8., 7., 6.],
          [5., 4., 3., 4., 5., 4., 3.],
          [2., 1., 0., 1., 2., 1., 0.],
          [5., 4., 3., 4., 5., 4., 3.],
          [8., 7., 6., 7., 8., 7., 6.],
          [5., 4., 3., 4., 5., 4., 3.],
          [2., 1., 0., 1., 2., 1., 0.]]]])
tensor([[[[0., 0., 0., 1., 2., 2., 2.],
          [0., 0., 0., 1., 2., 2., 2.],
          [0., 0., 0., 1., 2., 2., 2.],
          [3., 3., 3., 4., 5., 5., 5.],
          [6., 6., 6., 7., 8., 8., 8.],
          [6., 6., 6., 7., 8., 8., 8.],
          [6., 6., 6., 7., 8., 8., 8.]]]])

进程已结束,退出代码0

3.非线性激活 Non-linear Activations

3.1 torch.nn.ReLU 和 torch.nn.Sigmoid

应用整流的线性单位函数的元素
参数：

torch.nn.ReLU(inplace=False)
torch.nn.Sigmoid()

解析：
inplace ：可以有选择地进行就地操作。默认值。假的
形状：
input(∗)：其中∗表示任何数目的维度。
output(∗)：与输入的形状相同。

3.1.1 torch.nn.ReLU 和 torch.nn.Sigmoid 计算

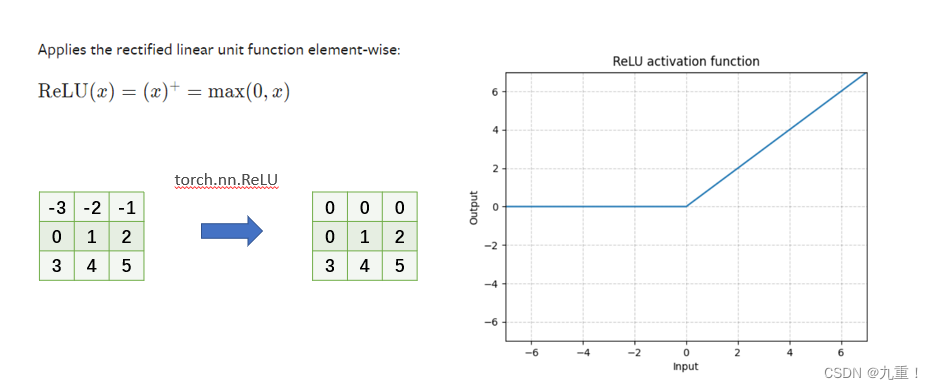
(1)torch.nn.ReLU
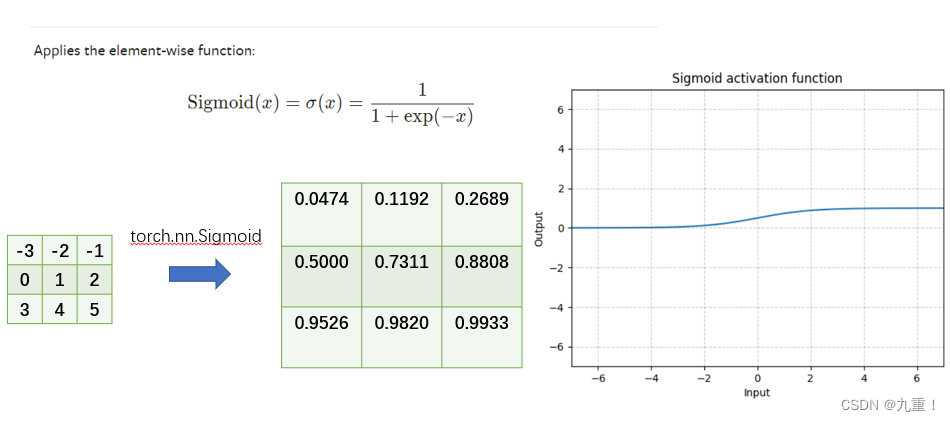
在这里插入图片描述
(2) torch.nn.Sigmoid

3.1.2 python 代码例子

3.1.2.1 上边的例子复现代码

from torch import nn
import torch
m = nn.ReLU()
mm = nn.Sigmoid()

input = torch.arange(-3, 6, dtype=torch.float).reshape(1, 1, 3, 3)
print(input)
output = m(input)
output2 = mm(input)
print(output)
print(output2)

输出结果：

tensor([[[[-3., -2., -1.],
          [ 0.,  1.,  2.],
          [ 3.,  4.,  5.]]]])
tensor([[[[0., 0., 0.],
          [0., 1., 2.],
          [3., 4., 5.]]]])
tensor([[[[0.0474, 0.1192, 0.2689],
          [0.5000, 0.7311, 0.8808],
          [0.9526, 0.9820, 0.9933]]]])

进程已结束,退出代码0

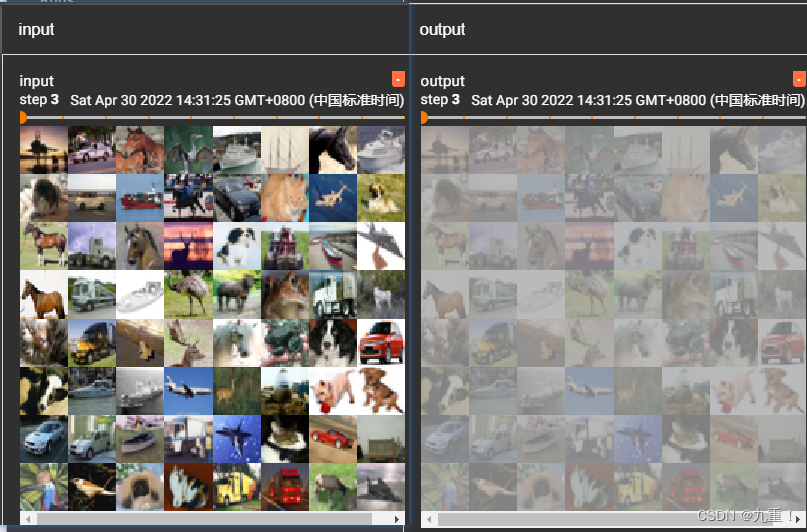
3.1.2.2 CIFAR10数据集合的一个例子

import torch
from torch.utils.tensorboard import SummaryWriter
import torchvision
from torch.utils.data import DataLoader
from torch import nn

dataset = torchvision.datasets.CIFAR10("./dataset", train=False, transform=torchvision.transforms.ToTensor(),
                                       download=True)
dataloader = DataLoader(dataset, batch_size=64)


class example(nn.Module):
    def __init__(self):
        super(example, self).__init__()
        self.Sigmoid1 = nn.Sigmoid()

    def forward(self, x):
        x = self.Sigmoid1(x)
        return x


jiuchong = example()

writer = SummaryWriter("./logs")
step = 0
for data in dataloader:
    imgs, targets = data
    outputs = jiuchong(imgs)
    print(imgs.shape)
    print(outputs.shape)
    writer.add_images("input", imgs, step)
    writer.add_images("output", outputs, step)
    step = step + 1

输出结果：
在这里插入图片描述

4. 归一化层Normalization Layers

归一化是什么？为什么要归一化？
如论文《批量归一化》中所述进行批量归一化。通过减少内部协变量偏移来加速深度网络训练。
简单举个例子简单理解下：
在这里插入图片描述
以上三张图相同？当然不相同，每个像素点都不相同。但是它们要表达的信息都相同：一只猫。在神经网络训练的过程中，我们主要的就是提取其本质的信息，重要的信息。
在上边三张图中，其数据信息不尽相同。因此需要将不同的信息去掉，尽可能提取我们需要的信息部分，所以引入了正则化。
正则化操作：
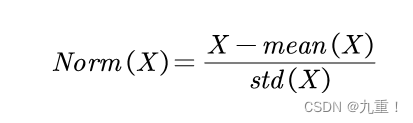
在这里插入图片描述

4.1 torch.nn.BatchNorm2d

如论文《批量归一化》中所述，对4D输入（具有额外通道维度的小型批量2D输入）进行批量归一化。通过减少内部协变量偏移来加速深度网络训练。
参数：

torch.nn.BatchNorm2d(num_features, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True, device=None, dtype=None)

解析：
num_features ：从预期输入的大小(N,C,H,W)中得到的C。

eps ：为了数值的稳定性而加到分母上的一个数值。默认值：1e-5

momentum ：用于running_mean和running_var计算的值。对于累积移动平均数（即简单平均数）可以设置为无。默认值：0.1。

affine ：一个布尔值，当设置为True时，这个模块有可学习的仿生参数。默认值。真

track_running_stats ：一个布尔值，当设置为True时，本模块跟踪运行中的平均值和方差，当设置为False时，本模块不跟踪此类统计，并将统计缓冲区running_mean和running_var初始化为None。当这些缓冲区为 "无 "时，本模块总是使用批处理统计，在训练和评估模式下都是如此。默认值。真

（1）计算公式
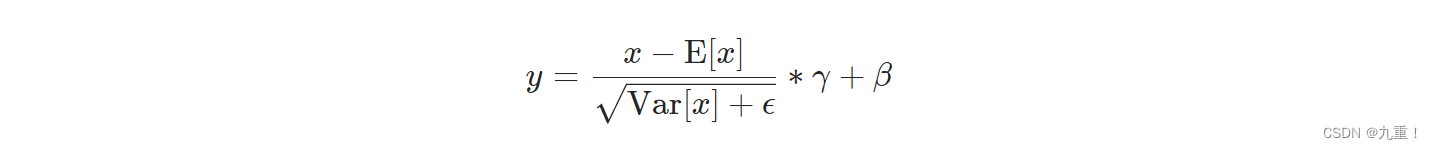
在这里插入图片描述
每个维度的平均数和标准差都是按小批量计算的。γ和β是大小为C的可学习参数向量（其中C是输入大小）。默认情况下，γ的元素被设置为1，β的元素被设置为0。标准差是通过有偏估计器计算的，相当于torch.var(input, unbiased=False)。
另外，默认情况下，在训练期间，该层保持其计算的平均值和方差的运行估计值，然后在评估期间用于归一化。运行估计值的默认动量为0.1。
如果track_running_stats被设置为False，那么这个层就不会保持运行估计，而在评估时间内也会使用批处理统计。

这个动量参数与优化器类中使用的动量参数和传统的动量概念不同。在数学上，这里运行统计的更新规则是：
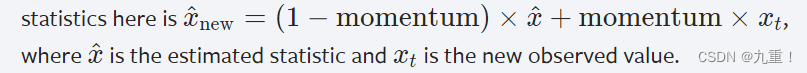
在这里插入图片描述
因为批量归一化是在C维上进行的，计算（N，H，W）片上的统计数据，所以通常的术语是把这称为空间批量归一化。
【PS：好吧，以上的官方文档可能有些地方没有看明白…下边在重新提下】

（1）其中参数num_features就比较好理解了，就是通道C。eps也不难理解就是Var[x]加上一个小的偏置，干嘛用的呢？简单理解就是为了让分母不为零。
（2）affine：首先需要知道的Norm的公式就是：
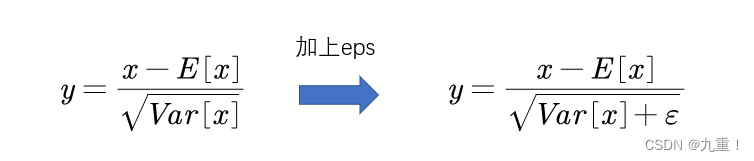
在这里插入图片描述
但是有个问题：我们在进行训练的，使用的是随机梯度下降的训练。在训练的过程当中E[x],Var[x]不是所有数据的均值和方差，只是一小部分的数据的均值和方差。因此在在最终算得的norm在乘以γ，加上β。

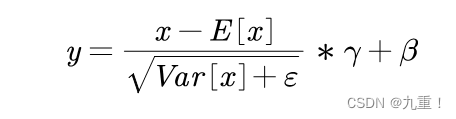
γ相当于对Var[x]进行修正。加上β相当于E[x]进行修正。其中γ，β是可以学习两个参数。若参数affine为False，就γ，β不学习即γ=1，β=0就是一个常量。若参数affine为True，就γ，β可以进行学习即γ，β就是变量了。在训练的过程中通过梯度下降对γ，β进行更新
（3）track_running_stats ：对应E[x]，Var[x]只是一小部分的数据的均值和方差。因此需要对于x进行修正：因此计算E[x]，Var[x]是经过修正的x。
在这里插入图片描述
track_running_stats为True，对X进行修正。为False不进行。momentum 就是x修正公式中momentum。
（4）在BatchNorm2d 中沿着（N，H，W）的维度计算均值方差。

4.1.1 运算例子

import torch
from torch import nn

eps =1e-5
inputs = torch.randn(3,5,6,2) # 随机生成

inputs_mean = torch.mean(inputs,[0,2,3],keepdim=True)   # 0，2，3 维度进行计算均值

inputs_var = torch.var(inputs,[0,2,3],keepdim=True,unbiased=False)  # 0，2，3 维度进行计算方差

out = (inputs-inputs_mean)/torch.sqrt(inputs_var+eps)   # 归一化
print(out)

#BatchNorm2d进行的归一化，其中affine=False,track_running_stats=False
jiuchong = nn.BatchNorm2d(5, affine=False,track_running_stats=False)  
out2 =jiuchong(inputs)
print(out2)

#计算两者平均差值
print(torch.mean(out-out2))

输出结果：
out：

tensor([[[[ 3.0536e+00, -2.4068e-01],
          [ 7.0966e-01,  5.5591e-01],
          [ 7.3400e-01,  8.8354e-01],
          [-2.3530e-01,  5.7989e-01],
          [ 6.8488e-01, -2.7980e-02],
          [ 1.8442e+00, -1.8052e-01]],
          ....
           [[ 1.6221e+00, -1.4393e+00],
          [ 5.9213e-02, -3.3249e-01],
          [ 4.5410e-01,  3.5074e-01],
          [ 2.5822e-01,  3.3709e-01],
          [ 6.8354e-01, -7.2697e-01],
          [-6.1930e-01,  2.2866e-01]]]])

out2：

tensor([[[[ 3.0536e+00, -2.4068e-01],
          [ 7.0966e-01,  5.5591e-01],
          [ 7.3400e-01,  8.8354e-01],
          [-2.3530e-01,  5.7989e-01],
          [ 6.8488e-01, -2.7980e-02],
          [ 1.8442e+00, -1.8052e-01]],
          ....
           [[ 1.6221e+00, -1.4393e+00],
          [ 5.9213e-02, -3.3249e-01],
          [ 4.5410e-01,  3.5074e-01],
          [ 2.5822e-01,  3.3709e-01],
          [ 6.8354e-01, -7.2697e-01],
          [-6.1930e-01,  2.2866e-01]]]])

两者平均差值

tensor(4.4639e-09)

4.2 torch.nn.InstanceNorm2d

参数：

torch.nn.InstanceNorm2d(num_features, eps=1e-05, momentum=0.1, affine=False, track_running_stats=False, device=None, dtype=None)

解析：
num_features - 从一个预期大小为(N,C,H,W)或(C,H,W)的输入的C。

eps - 为了数值的稳定性而加到分母上的一个数值。默认值：1e-5

momentum - 用于running_mean和running_var计算的值。默认值：0.1

affine - 一个布尔值，当设置为 "True "时，该模块有可学习的仿生参数，初始化的方式与批量规范化的方式相同。默认值。为假。

track_running_stats - 一个布尔值，当设置为True时，该模块会跟踪运行中的平均值和方差，当设置为False时，该模块不会跟踪这些统计数据，在训练和评估模式下都会使用批量统计。默认值。False

（1）计算公式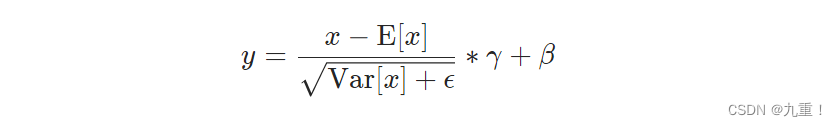 在这里插入图片描述
平均数和标准差是针对小批量中的每个物体分别计算的。γ和β是大小为C（其中C是输入大小）的可学习参数向量，如果affine是True的话。标准差是通过有偏估计器计算的，相当于torch.var(input, unbiased=False)。
默认情况下，该层在训练和评估模式下都使用从输入数据中计算出的实例统计数据。
如果track_running_stats被设置为True，在训练过程中，该层会保持其计算的平均值和方差的运行估计值，然后在评估过程中用于归一化。运行估计值的默认动量为0.1。

【PS：看到这里感觉和torch.nn.BatchNorm2d很像。不同的在BatchNorm2d 中沿着（N，H，W）的维度计算均值方差。而torch.nn.InstanceNorm2d是沿着【H，W】的维度计算均值方差。】

4.2.1 运算例子

import torch
from torch import nn

eps =1e-5
inputs = torch.randn(3,5,6,2) # 随机生成

inputs_mean = torch.mean(inputs,[2,3],keepdim=True)   # 0，2，3 维度进行计算均值

inputs_var = torch.var(inputs,[2,3],keepdim=True,unbiased=False)  # 0，2，3 维度进行计算方差

out = (inputs-inputs_mean)/torch.sqrt(inputs_var+eps)   # 归一化
print(out)

#InstanceNorm2d进行的归一化，其中affine=False,track_running_stats=False
jiuchong = nn.InstanceNorm2d(5, affine=False,track_running_stats=False)
out2 =jiuchong(inputs)
print(out2)

#计算两者平均差值
print(torch.mean(out-out2))

本文作者：九重！
本文链接：https://blog.csdn.net/weixin_43798572/article/details/124509977
关于博主：评论和私信会在第一时间回复。或者直接私信我。
声援博主：如果您觉得文章对您有帮助，可以点击文章右下角【点赞】【收藏】一下。您的鼓励是博主的最大动力！