卷积码的基本原理

        卷积码是1955 年由Elias提出的，又由Forney完成其代数理论基础研究工作。

卷积码的编码过程中，本组中的校验比特不仅与本组中的信息比特有关，而且还与以前各时刻输入至编码器的信息比特有关。同样，在卷积码译码过程中，不仅从此时刻收到的码组中提取译码信息，而且还要利用以前或以后各时刻收到的码组提取相关信息。

        正由于卷积码编码过程中充分利用了每个码组之间的相关性，因此，在与分组码同样的码率和设备条件下，无论从理论上还是实际上均证明了卷积码的性能优于分组码。

        由于卷积码能够简化编译码电路，并得到较好的差错控制性能，因此卷积码在通信领域，特别是在卫星通信，空间通信领域得到了广泛的应用。

1 卷积码的基本概念

        通常情况下，卷积码可以记为(n, k,m)，表示卷积码码字中码元的个数为n，码字中信息元个数为k，编码器由m−1级移位寄存器构成。

m 称为卷积码的约束长度，它是表示卷积码编码器复杂性的一个重要参数。约束长度越大，编码器和译码器越复杂，但卷积码的纠错能力也越强。因此这是一个矛盾，在具体设计时要根据应用要求进行折中处理，选择适当的码型。

        卷积码的码率定义为R = k/n，它表示卷积码的编码效率。卷积码可分为系统码和非系统码，将k个信息比特放在最左边，n − k 个校验比特放在右边，组成一个码字，这就是系统码的形式。

2 卷积码的表示方法

卷积码的表示方法主要有多项式矩阵表示法、状态图表示法和网格图表示法三种

        多项式矩阵表示的方法多用于介绍卷积码的代数译码方式，而在介绍Viterbi译码算法时习惯于采用网格图表示方法，因为它比较直观的表现了编译码过程中各状态的转移关系。

        以简单的(2,1,3)卷积码编码器为例，其生成约束关系多项式表示为：

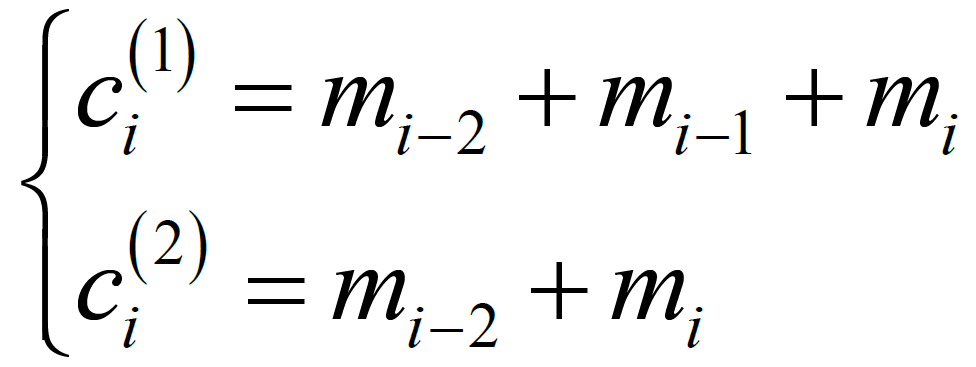
        卷积码的编码器是一个时序网络，其工作过程可以用一个状态图来描述，编码器的状态由它的移位寄存器的内容确定。状态图表示的方法提供了一个比较直观的完整的编码系统描述，但是它的缺点是不能描述随着时间变化系统状态转移的轨迹。例如(2,1,3)卷积码，有k个信息位，m-1 位移位寄存器，共有

个不同状态。其状态可以表示为

分别为 。根据(2,1,3)卷积码的生成多项式或生成矩阵，可以确定它的唯一的状态图如下图所示。

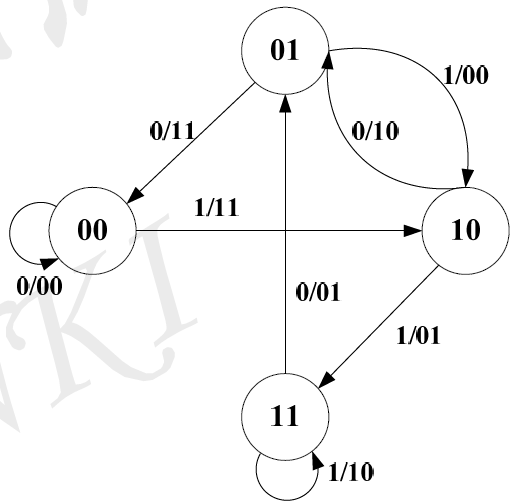
        其中状态转移线上的数字表示某一时刻编码器输入某一信息位后编码器输出的码元序列。
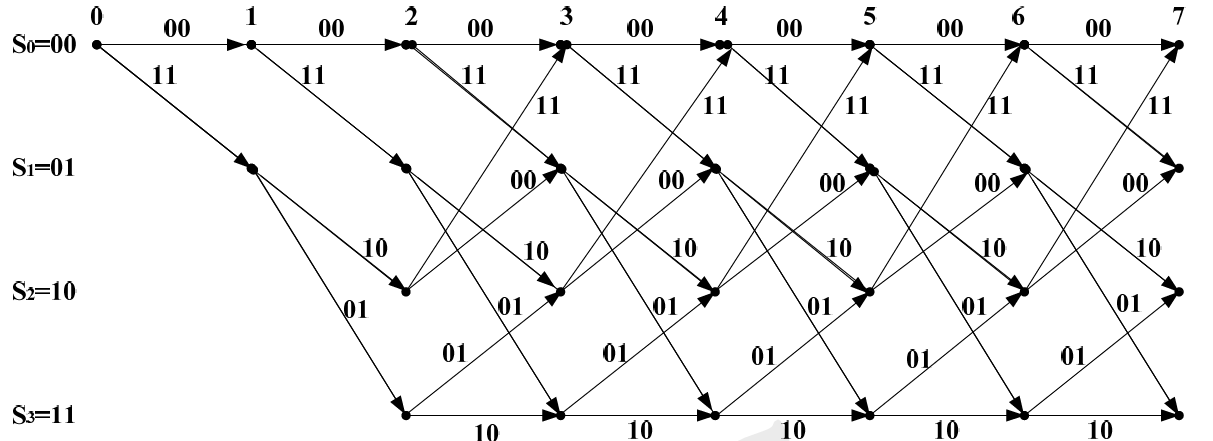
        卷积码的另一种表示方法是网格图表示法，这是一种将编码器的状态图按时间展开的方法。

网格图以状态为纵轴，以时间为横轴，描述了状态转移和转移发生时的输入信息与输出码组的关系。

        对于一般的(n, k,m)卷积编码器来说，网格图有个不同状态，从每个状态出发条分支，每条分支上标有n比特输出码字。

        网格图与状态图比较优点就在于可以体现时间的变化，体现编码的全过程，因此在译码过程中起了很重要的作用。
        下图所示的网格图画出了各种可能的输入信息序列，(2,1,3)编码器全部可能的状态转移的轨迹。网格图的中间状态均为两个输入分支和两个输出分支，对于每个状态的输出分支，上分支表示输入的信息位为0，下分支表示输入的信息位为1。