参照 中序线索二叉树
整体思路和中序线索二叉树差不多
如何在先序线索二叉树中找到结点的后继?
结点p的后继:
- p有左孩子,即p->ltag==0,则左孩子即为后继
- p无左孩子,则右指针rchild即为p在先序下的后继结点,
prchild要么指向右孩子(右孩子其实也是在先序下的后继结点),要么指向p在先序 下的后继结点
只是在先序线索void PreThread(ThreadTree &p,ThreadTree &pre)要注意添加tag的判断,不然可能会出现死循环,如下代码段所示
if(p->ltag != 1)//@@@ 这里因为p->lchild可能是p的前驱结点,//如果不判断ltag,则会死循环,
PreThread(p->lchild,pre);//递归,线索化左子树
if(p->rtag != 1)//@@@
PreThread(p->rchild, pre);//递归,线索化右子树
完整测试代码
//先序线索二叉树
#include<stdio.h>
#include<stdlib.h>
#define ElemType char
//tag为0表示指向左/右孩子,为1表示指向结点的前驱/后继
typedef struct ThreadNode{
ElemType data;//数据元素
struct ThreadNode *lchild,*rchild;//左右孩子指针
int ltag;//因为定义结构体时,并未给其分配内存,所以初值是无法存储的。应该声明结构体变量后,手工赋值
int rtag;//左右线索标记
}ThreadNode,*ThreadTree;
void visit(ThreadTree T){
printf("%c ",T->data);
}
//先序线索二叉树的构造, 根左右
void PreThread(ThreadTree &p,ThreadTree &pre){
if(p){
if(p->lchild == NULL){//左子树为空,建立前驱线索
p->lchild=pre;
p->ltag=1;
}
if(pre!=NULL && pre->rchild==NULL){
pre->rchild=p;//建立前驱结点的后继线索
pre->rtag=1;
}
pre=p;//标记当前结点成为刚刚访问过的结点
if(p->ltag != 1)//@@@ 这里因为p->lchild可能是p的前驱结点,
//如果不判断ltag,则会死循环,
PreThread(p->lchild,pre);//递归,线索化左子树
if(p->rtag != 1)//@@@
PreThread(p->rchild, pre);//递归,线索化右子树
}//if(p != NULL)
}
//通过先序遍历建立先序线索二叉树的主过程算法如下:
void CreatePreThread(ThreadTree &T){
ThreadTree pre=NULL;
if(T){ //非空二叉树,线索化
PreThread(T,pre);//线索化二叉树
pre->rchild==NULL;//处理遍历的最后一个结点
pre->rtag=1;
//printf("CreatePreThread Finished\n");
}
}
//求先序线索二叉树中,先序序列下的第一个结点
ThreadNode *Firstnode(ThreadNode *p){
return p;
}
//求先序线索二叉树中,结点p在先序序列下的后继
/*p的后继:
1. p有左孩子,即p->ltag==0,则左孩子即为后继
2. p无左孩子,则右指针rchild即为p在先序下的后继结点,
prchild要么指向右孩子(右孩子其实也是在先序下的后继结点),要么指向p在先序下的后继结点
*/
ThreadNode *Nextnode(ThreadNode *p){
if(p->ltag==0){//左孩子指针
return Firstnode(p->lchild);
}
else{// ltag==1 直接返回后继线索
return p->rchild;
}
}
//利用上面的两个算法,
//可以写出不含头结点的先序线索二叉树的先序遍历算法
void Preorder(ThreadNode *T){
for(ThreadNode *p=Firstnode(T);p!=NULL;p=Nextnode(p)){
visit(p);
}
}
//创建线索二叉树,按前序输入, #表示空节点
bool CreateThreadTree(ThreadTree &T){
ElemType ch;
scanf("%c", &ch);
if(ch == '#'){
//printf("您要创建一棵空树吗?\n");
T=NULL;
return false;
}
else{
T=(ThreadTree)malloc(sizeof(ThreadNode));
T->ltag=T->rtag=0;
if(!T){
printf("malloc failure\n");
return false;
}
T->data = ch;
CreateThreadTree(T->lchild);
CreateThreadTree(T->rchild);
return true;
}
}
//后序销毁
bool DestroyThreadTree(ThreadTree T){
if(T==NULL){
printf("空节点\n");
return false;
}
if(T->ltag!=1)//@@@
DestroyThreadTree(T->lchild);
if(T->rtag!=1)//@@@
DestroyThreadTree(T->rchild);
printf("销毁%c\n",T->data);
free(T);//@@@'
T=NULL;
return true;
}
//先序递归遍历线索二叉树
void PreOrder(ThreadTree T){
if(T){
visit(T);
if(T->ltag!=1)
PreOrder(T->lchild);
if(T->rtag != 1)
PreOrder(T->rchild);
}
}
int main(){
ThreadTree T=NULL;
printf("按前序输入二叉树中节点的值(输入#表示空节点)\n");
CreateThreadTree(T);//输入前序,建立二叉树
CreatePreThread(T);//通过先序遍历建立先序线索二叉树
ThreadNode *p=Firstnode(T);//求先序遍历下的第一个结点
printf("\n先序遍历的第一个结点p: %c\n",p->data);
ThreadNode* r=Nextnode(p);//求中序遍历下p的后继
printf("p的后继r: %c\n",r->data);
printf("先序遍历线索二叉树(递归PreOrder ≈ 正常BinaryTree遍历): \n");
PreOrder(T);
printf("\n");
printf("\n先序遍历线索二叉树(非递归Preorder ≈ Firstnode+Nextnode): \n");
Preorder(T);
printf("\n用完要记得销毁哦!\n");
DestroyThreadTree(T);
return 0;
}
测试样例:

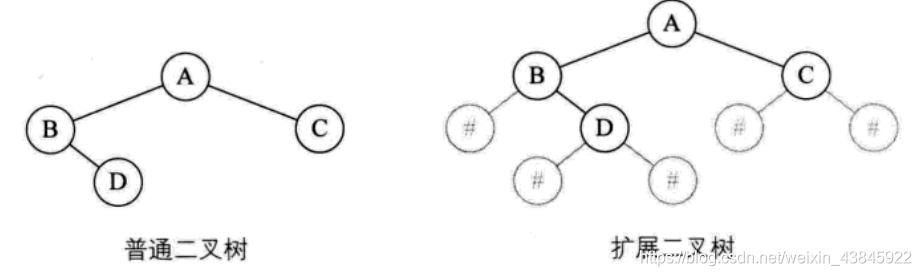
测试结果
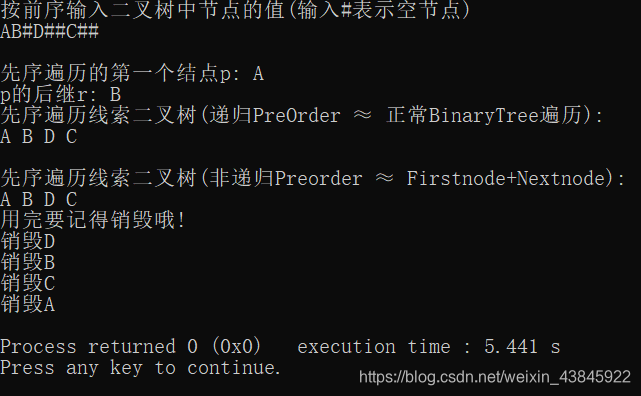
























 5756
5756

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








