【BI学习心得09-时间序列分析】

最新推荐文章于 2024-04-15 08:52:36 发布

水花

最新推荐文章于 2024-04-15 08:52:36 发布

阅读量6.2k

点赞数 1

分类专栏： BI_推荐系统文章标签： python 时间序列推荐系统

本文链接：https://blog.csdn.net/weixin_43849871/article/details/112117209

版权

BI_推荐系统专栏收录该内容

49 篇文章 15 订阅

订阅专栏

写在前面的话

如果你是一个股民，某只股票的股价就是一类时序数据，其记录着每个时间点该股票的股价。
如果你是一个运维人员，监控数据是一类时序数据，例如对于机器的CPU的监控数据，就是记录着每个时间点机器上CPU的实际消耗值。

这个世界是由数据构成的，在这个世界上存在的每个物体，每时每刻都在产生着数据。而对这些数据的挖掘和利用，在这个时代，正在默默的改变人们的生活方式。例如通过可穿戴设备对个人健康的管理，就是通过设备不断采集你的个人健康数据，例如心跳、体温等等，收集完数据后套用模型计算来评估你的健康度。

如果你的视野和想象空间足够大，你会发现你能够挖掘并利用的数据充斥在你所生活的环境中。这些能够产生数据的对象，会包括你的手机、汽车、空调、冰箱等等。当前比较火热的物联网的核心思想，其实就是构建一个可以让所有物体生产数据并挖掘其价值的网络。而通过这个网络采集的数据，就是典型的时序数据。

时序数据用于描述一个物体在历史的时间维度上的状态变化信息，而对于时序数据的分析，就是尝试掌握并把控其变化的规律的过程。随着物联网、大数据和人工智能技术的发展，时序数据也呈一个爆发式的增长。而为了更好的支持这类数据的存储和分析，在市场上衍生出了多种多样的新兴的数据库产品。这类数据库产品的发明都是为了解决传统关系型数据库在时序数据存储和分析上的不足和缺陷，这类产品被统一归类为时序数据库。

1.时间序列

1.1时间序列的概念

时间序列是按照时间排序的一组随机变量，它通常是在相等间隔的时间段内依照给定的采样率对某种潜在过程进行观测的结果。时间序列数据本质上反映的是某个或者某些随机变量随时间不断变化的趋势，而时，间序列预测方法的核心就是从数据中挖掘出这种规律，并利用其对将来的数据做出估计。

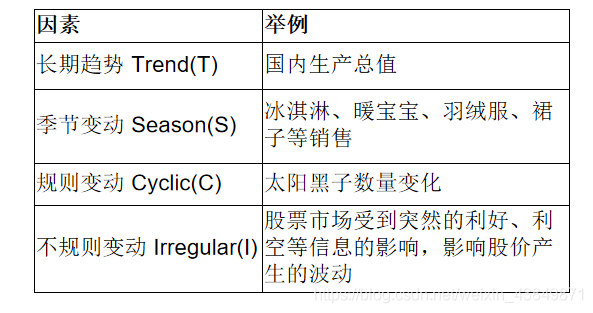
构成要素：长期趋势，季节变动，循环变动，不规则变动。

1）长期趋势（ T ）现象在较长时期内受某种根本性因素作用而形成的总的变动趋势。
2）季节变动（ S ）现象在一年内随着季节的变化而发生的有规律的周期性变动。
3）循环变动（ C ）现象以若干年为周期所呈现出的波浪起伏形态的有规律的变动。
4）不规则变动（I ）是一种无规律可循的变动，包括严格的随机变动和不规则的突发性影响很大的变动两种类型。
在这里插入图片描述

时间序列在金融、经济、商业领域拥有广泛的应用：

机器学习模型，包括AR、MA、ARMA、ARIMA
神经网络模型，用LSTM进行时间序列预测

1.2时间序列的不同分类

时间序列是按时间顺序排列的、随时间变化且相互关联的数据序列。分析时间序列的方法构成数据分析的一个重要领域，即时间序列分析。时间序列根据所研究的依据不同，可有不同的分类。

1．按所研究的对象的多少分，有一元时间序列和多元时间序列。

2．按时间的连续性可将时间序列分为离散时间序列和连续时间序列两种。

3．按序列的统计特性分，有平稳时间序列和非平稳时间序列。如果一个时间序列的概率分布与时间t无关，则称该序列为严格的（狭义的）平稳时间序列。如果序列的一、二阶矩存在，而且对任意时刻t满足：

（1）均值为常数

（2）协方差为时间间隔 $\small \tau$ 的函数。则称该序列为宽平稳时间序列，也叫广义平稳时间序列。我们以后所研究的时间序列主要是宽平稳时间序列。

4．按时间序列的分布规律来分，有高斯型时间序列和非高斯型时间序列。

2.移动平均法

移动平均法可以作为一种数据平滑的方式 ,以每天的气温数据为例，今天的天气可能与过去的十天的气温有线性关系；或者有的人对食物有一种节俭的美德，他们做的饭菜能看出有些是上一顿的，当然也有一部分是今天的做的，再假设隔两顿的都被倒掉了，并且每天都是这样的，那么这碗饭菜可能就是一部分上一顿的再加上一部分今天现做的，这就是一个一阶的移动平均。

移动平均法是根据时间序列资料逐渐推移，依次计算包含一定项数的时序平均数，以反映长期趋势的方法。当时间序列的数值由于受周期变动和不规则变动的影响，起伏较大，不易显示出发展趋势时，可用移动平均法，消除这些因素的影响，分析、预测序列的长期趋势。移动平均法有简单移动平均法，加权移动平均法，趋势移动平均法等。

2.1简单移动平均法

在这里插入图片描述
近N 期序列值的平均值作为未来各期的预测结果。一般 N 的取值范围： 5≤N≤ 200。当历史序列的基本趋势变化不大且序列中随机变动成分较多时，N 的取值应较大一些。否则 N 的取值应小一些。在有确定的季节变动周期的资料中，移动平均的项数应取周期长度。选择佳 N 值的一个有效方法是，比较若干模型的预测误差。预测标准误差小者为好。

简单移动平均法只适合做近期预测，而且是预测目标的发展趋势变化不大的情况。如果目标的发展趋势存在其它的变化，采用简单移动平均法就会产生较大的预测偏差和滞后。

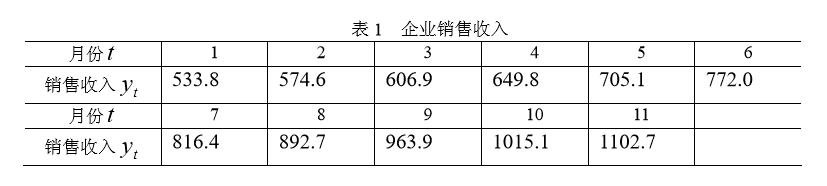
例1 某企业 1月~11月份的销售收入时间序列如表1所示。使用一次简单滑动平均法预测12月份的销售收入。

在这里插入图片描述

2.2加权移动平均法

在简单移动平均公式中，每期数据在求平均时的作用是等同的。但是，每期数据所包含的信息量不一样，近期数据包含着更多关于未来情况的信心。因此，把各期数据等同看待是不尽合理的，应考虑各期数据的重要性，对近期数据给予较大的权重，这就是加权移动平均法的基本思想。

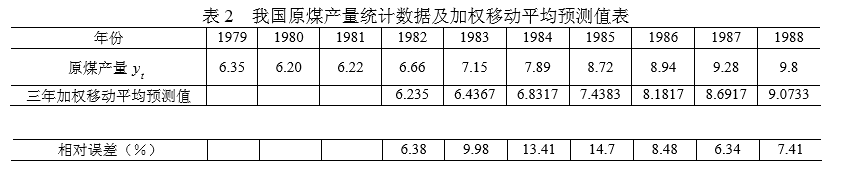
在这里插入图片描述
例 2 我国 1979～1988 年原煤产量如表 2 所示，试用加权移动平均法预测 1989 年的产量

在这里插入图片描述

在加权移动平均法中, $\small w_{t}$ 的选择，同样具有一定的经验性。一般的原则是：近期数据的权数大，远期数据的权数小。至于大到什么程度和小到什么程度，则需要按照预测者对序列的了解和分析来确定。

2.3趋势移动平均法

简单移动平均法和加权移动平均法，在时间序列没有明显的趋势变动时，能够准确反映实际情况。但当时间序列出现直线增加或减少的变动趋势时，用简单移动平均法和加权移动平均法来预测就会出现滞后偏差。因此，需要进行修正，修正的方法是作二次移动平均，利用移动平均滞后偏差的规律来建立直线趋势的预测模型。这就是趋势移动平均法。一次移动的平均数为

在这里插入图片描述

例 3 我国 1965～1985 年的发电总量如表 3 所示，试预测 1986 年和 1987 年的发电总量。

解由散点图 1 可以看出，发电总量基本呈直线上升趋势，可用趋势移动平均法来预测。

趋势移动平均法对于同时存在直线趋势与周期波动的序列，是一种既能反映趋势变化，又可以有效地分离出来周期变动的方法。

3.指数平滑法

指数平滑法是在移动平均法基础上发展起来的一种时间序列分析预测法，它是通过计算指数平滑值，配合一定的时间序列预测模型对现象的未来进行预测，其原理是任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均。利用修匀技术，削弱短期随机波动对序列的影响，使序列平滑化，从而显示出长期趋势变化的规律。

用序列过去值的加权均值来预测将来的值，序列中近期的数据被赋以较大的权重，远期的数据被赋以较小的权重。理由是一般情况下，某一变量值对其后继行为的影响作用是逐渐衰减的。

3.1基础知识

前提假设：时间序列分析一般假设我们获得的数据在时域上具有一定的相互依赖关系，例如股票价格在t时刻很高，那么在t+1时刻价格也会比较高（跌停才10%）；如果股票价格在一段时间内获得稳定的上升，那么在接下来的一段时间内延续上升趋势的概率也会比较大。
目标：（1）发现这种隐含的依赖关系，并增加我们对此类时间序列的理解；（2）对未观测到的或者尚未发生的时间序列进行预测。

我们认为时间序列由两部分组成：有规律的时间序列（即有依赖关系）+噪声（无规律，无依赖）。所以，接下来要做的就是过滤噪声：

最简单的 $\color{red}过滤噪声$ 的方法是：取平均。

3.2简单滑动平均（rolling mean）

特点：当窗口取得越长，噪声被去除的就越多，我们得到的信号就越平稳；但同时，信号的有用部分丢失原有特性的可能性就越大，而我们希望发现的规律丢失的可能性就越大。
缺点：（1）我们要等到至少获得T个信号才能进行平均，那么得到的新的信号要比原始信号短；（2）在得到S_t的时候，我们只有距离t最近的T个原始信号。但在原始信号中，可能信号之间的相互依赖关系会跨越非常长的时间长度，比如X_1可能会对X_100会产生影响，这样滑动平均就会削弱甚至隐藏这种依赖关系。

3.2指数平均(EXPMA)

接下来介绍一种稍微复杂但能克服以上缺点并且在现实中应用也更加广泛的方法：指数平均（exponential smoothing，也叫exponential weighted moving average ），这种平均方法的一个重要特征就是，S_t与之前产生的所有信号有关，并且距离越近的信号所占权重越大。

3.2.1一阶指数平滑

当时间数列无明显的趋势变化，可用一次指数平滑预测。

一阶指数平滑实际就是对历史数据的加权平均，它可以用于任何一种 $\color{red}没有明显函数规律但确实存在某种前后关联$ 的时间序列的 $\color{red}短期预测$ 。其预测公式为：（任一期的指数平滑值都是本期实际观察值与前一期指数平滑值的加权平均）

$y_{t+1}'=a*y_{t}+(1-a)*y_{t}' \ \ 或者alt="S_{t}^{(1)}=a*y_{t}+(1-a)*S_{t-1}^{(1)}"$

a：平滑系数
yt+1’：t+1期的预测值，即本期（t期）的平滑值
St ； yt：t期的实际值；
yt’：t期的预测值，即上期的平滑值St-1 。 $\color{red}本期的平滑值 = 下期的预测值$

该公式又可以写作：

$y_{t+1}'=y_{t}'+a*(y_{t}-y_{t}')$

可见：下期预测值是本期预测值与以a为折扣的本期实际值与预测值误差之和。

最突出的优点：方法非常简单，甚至只要样本末期的平滑值，就可以得到预测结果。
一次指数平滑的特点是：能够跟踪数据变化。这一特点所有指数都具有。预测过程中添加最新的样本数据后，新数据应取代老数据的地位，老数据会逐渐居于次要的地位，直至被淘汰。这样，预测值总是反映最新的数据结构。
一次指数平滑有局限性：第一，预测值不能反映趋势变动、季节波动等有规律的变动；第二，这种方法多适用于短期预测，而不适合作中长期的预测；第三，由于 $\color{red}预测值是历史数据的均值$ ，因此与实际序列的变化相比有 $\color{red}滞后现象$ 。
平滑系数：指数平滑预测是否理想，很大程度上取决于平滑系数。指数平滑法对实际序列具有平滑作用，平滑系数a 越小，平滑作用越强，但对实际数据的变动反应较迟缓。

EViews提供两种确定指数平滑系数的方法： $\color{red}自动给定和人工确定$ 。选择自动给定，系统将按照 $\color{red}预测误差平方和最小原则$ 自动确定系数。如果系数接近1，说明该序列近似纯随机序列，这时最新的观测值就是最理想的预测值。出于预测的考虑，有时系统给定的系数不是很理想，用户需要自己指定平滑系数值。一般来说：

（1）如果序列变化比较平缓，平滑系数值应该比较小，比如小于0.1；
（2）如果序列变化比较剧烈，平滑系数值可以取得大一些，如0.3～0.5；
（3）若平滑系数值大于0.5才能跟上序列的变化，表明序列有很强的趋势，不能采用一次指数平滑进行预测。

缺点：（1）只考虑历史平均，不考虑变化趋势；（2）在实际序列的线性变动部分，指数平滑值序列出现一定的滞后偏差，偏差程度随着平滑系数a 的增大而减少，但当时间序列的变动出现直线趋势时，用一次指数平滑法来进行预测仍将存在明显的滞后偏差。因此，也需要进行修正。

$\color{red}修正的方法$ 也是在一次指数平滑的基础上再进行二次指数平滑，利用滞后偏差的规律找出曲线的发展方向和发展趋势，然后建立直线趋势预测模型，故称为二次指数平滑法。

3.2.2二次指数平滑

二次指数平滑是对一次指数平滑的再平滑，同时考虑历史平均和变化趋势。它适用于具线性趋势的时间数列。

我们可以看到，虽然一次指数平均在产生新的数列的时候考虑了所有的历史数据，但是仅仅考虑其静态值，即没有考虑时间序列当前的变化趋势。如果当前的股票处于上升趋势，那么当我们对明天的股票进行预测的时候，好的预测值不仅仅是对历史数据进行”平均“，而且要考虑到当前数据变化的上升趋势。同时考虑历史平均和变化趋势，这便是二阶指数平均，公式：

$y_{t+m}=(2+\frac{am}{1-a})y_{t}'-(1+\frac{am}{1-a})y_{t}=(2y_{t}'-y_{t})+m(y_{t}'-y_{t})\frac{a}{1-a}$

式中，
$y_{t}=a*y_{t-1}'+(1-a)*y_{t-1}$

也就是：

$\begin{array}{lcl} \hat{Y}_{t+T} &=& a_t+b_t * T \tag{$2$} \\ S_t^{(2)} &=& aS_t^{(1)}+ (1-a)S_{t-1}^{(2)} \\ \end{array}$
$\begin{cases} a_t &=& 2S_t^{(1)}-S_t^{(2)} \\ b_t &=& \frac{a}{1-a}(S_t^{(1)}-S_t^{(2)}) \tag{$3$} \end{cases}$

$\hat{Y}_{t+T}$ ：第t+T期预测值；
$T$ ：由t期向后推移期数；

显然，二次指数平滑是一直线方程，其截距为： $(2 y t^{'} - y t)$ ，斜率为： $\frac{(yt’-yt) a}{(1-a)}$ ，自变量为预测天数。

在一次指数平滑的基础上得二次指数平滑的计算公式为：

$S_t^{(2)} = aS_t^{(1)}+ (1-a)S_{t-1}^{(2)}$

$S_t^{(2)}$ ：第t周期的二次指数平滑值；
$S_t^{(1)}$ ：第t周期的一次指数平滑值；
$S_{t-1}^{(2)}$ ：第t-1周期的二次指数平滑值；
$a$ ：加权系数（也称为平滑系数）。

二次指数平滑法是对一次指数平滑值作再一次指数平滑的方法。它不能单独地进行预测，必须与一次指数平滑法配合，建立预测的数学模型，然后运用数学模型确定预测值。

3.2.3三次指数平滑预测

与前两种相比，我们多考虑一个因素：季节性效应（ Seasonality）。这种平均模型考虑的季节性效应在股票或者期货价格中都会比较常见，比如在过年前A股市场通常会交易比较频繁，在小麦成熟的时候小麦期货价格也会有比较明显的波动。但是，模型本身的复杂度也增加了其使用难度，我们需要一定的经验才能比较合理地设置其中复杂的参数。
三次指数平滑预测是二次平滑基础上的再平滑。其预测公式是：

$yt+m=\frac{am*(3yt’-3yt+yt)+[(6-5a)yt’-(10-8a)yt+(4-3a)yt]}{2(1-a)2+ (yt’-2yt+yt’)*a2m2/2(1-a)2}$

式中， $y t = a y t - 1 + (1 - a) y t - 1$

它们的基本思想都是： $\color{red}预测值是以前观测值的加权和，且对不同的数据给予不同的权，新数据给较大的权，旧数据给较小的权$ 。

3.2.4二次指数平滑法实例分析

表中第③栏是我国1978-1996年全社会客运量的资料，据期绘制散点图，见下图，可以看出，各年的客运量资料基本呈线性趋势，但在几个不同的时期直线有不同的斜率，因此考虑用变参数线性趋势模型进行预测。具体步骤如下：

$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ 单位：万人$

年份	时间t	全社会客运量y	各期的一次指数平滑值 $S_t^{(1)}$	各期的二次指数平滑值 $S_t^{(2)}$	at	bt	$\hat{y}_{t+1}=a_t+b_t$
①	②	③	④	⑤	⑥	⑦	⑧
			253993.0	253993.0
1978	1	253993	253993.0	253993.0	253993.0	0.0
1979	2	289665	275396.2	266834.9	283957.5	12841.9	253993.0
1980	3	341785	315229.5	295871.7	334587.3	29036.7	296799.4
1981	4	384763	356949.6	332518.4	381380.8	36646.8	363624.0
1982	5	428964	400158.2	373102.3	427214.2	40583.9	418027.5
1983	6	470614	442431.7	414699.9	470163.4	41597.6	467798.1
1984	7	530217	495102.9	462941.7	527264.1	48241.8	511761.1
1985	8	620206	570164.8	527275.5	613054.0	64333.8	575505.8
1986	9	688212	640993.1	595506.1	686480.1	68230.5	677387.8
1987	10	746422	704250.4	660752.7	747748.2	65246.6	754710.7
1988	11	809592	767455.4	724774.3	810136.4	64021.6	812994.8
1989	12	791376	781807.8	758994.4	804621.1	34220.1	874158.1
1990	13	772682	776332.3	769397.1	783267.5	10402.8	838841.2
1991	14	806048	794161.7	784255.9	804067.6	14858.8	793670.2
1992	15	860855	834177.7	814209.0	854146.4	29953.1	818926.3
1993	16	996630	931651.5	884674.5	978628.5	70465.5	884099.5
1994	17	1092883	1028390.4	970904.0	1085876.8	86229.6	1049094.0
1995	18	1172596	1114913.8	1057309.9	1172517.6	86405.8	1172106.3
1996	19	1245356	1193179.1	1138831.4	1247526.8	81521.5	1258923.5
1997	20	1326094	1272928.0	1219289.4	1326566.7	80458.0	1329048.3
1998	21	1378717	1336401.4	1289556.6	1383246.2	70267.2	1407024.7
1999	22	1394413	1371208.4	1338547.7	1403869.1	48991.1	1453513.4
2000	23	1478573	1435627.1	1396795.4	1474458.9	58247.7	1452860.1
2001	24	1534122	1494724.1	1455552.6	1533895.5	58757.2	1532706.6
2002	25	1608150	1562779.6	1519888.8	1605670.4	64336.2	1592652.8

（1）第一步，计算一次指数平滑值，取 $a=0.6,S_0^{(2)}=S_1^{(1)}=y_1=253993$ ，根据一次指数平滑公式 $S_t^{(1)}=a*y_t+(1-a)*S_{t-1}^{(1)}$ ，可计算各期的一次指数平滑预测值：

1978年： $S_1^{(1)}=0.6*y_1+0.4*S_0^{(1)}=0.6*253993+0.4*253993=253993$
1979年： $S_2^{(1)}=0.6*y_2+0.4*S_1^{(1)}=0.6*289665+0.4*253993=275396.2$
同理可得各年的一次指数平滑预测值，见表1中第④栏。

（2）第二步，根据（1）式和第一步计算的，计算各期的二次指数平滑值，见表1中第⑤栏。
1978年： $S_2^{(2)}=0.6*S_1^{(1)}+0.4*S_0^{(2)}=0.6*253993+0.4*253993=253993$
1979年： $S_2^{(2)}=0.6*S_2^{(1)}+0.4*S_1^{(2)}=0.6*275396+0.4*253993=266834.9$

其余各期以此类推。
（3）第三步，计算各期参数变量值α、b。根据（3）式，可计算各期的α、b，分别见表第⑥、第⑦栏。如
$\begin{cases} a_2-2S_2^{(1)}-S_2^{(2)} &= & 2*275396.2-266834.9=283957.5 \\ b_2 &=& \frac{a}{1-a}(S_2^{(1)}-S_2^{(2)})=\frac{0.6}{0.4}(275396.2-266834.9)=12841.9 \end{cases}$

（4）第四步，根据（4）式和（2）式分别求各期的趋势预测值，见表中最后一栏。如：

2000年预测值： $\hat{y}_{2 3}=a_{22}+b_{22}*1=1403869.1+148991.1=1452860$

外推预测，得到
2003年预测值： $\hat{y}_{26}=\hat{y}_{25+1}=a_{25}+b_{25}*1=1605670.4+64336.2=1670006.7$

2004年预测值： $\hat{y}_{27}=\hat{y}_{26+1}=a_{25}+b_{25}*2=1605670.4+64336.2*2=1734342.9$

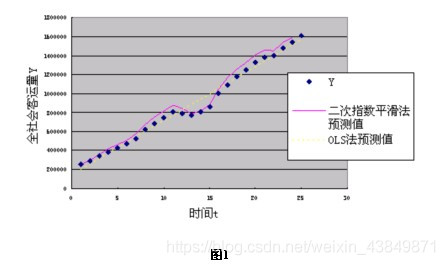
在这里插入图片描述

把各年的预测值绘成曲线与原时间序列的散点图比较（见上图），可以看出，二次指数平滑法由于考虑了时间序列在不同时期直线参数的变化，其预测值与原时间序列的拟合程度非常好。上图中也给出了用最小二乘法拟合的趋势直线，相比之下，用二次指数平滑法拟合的趋势线更好地体现了原时间序列在不同时间段的变化趋势。

4.平稳时间序列模型：自回归AR 、移动平均 MA 、ARMA 模型

4.1自回归AR(Auto Regressive)

认为过去若干时刻的点通过线性组合，再加上白噪声就可以预测未来某个时刻的点
日常生活环境中就存在白噪声，在数据挖掘的过程中，可以把它理解为一个期望为0，方差为常数的纯随机过程。

AR模型存在一个阶数p，称为AR§模型，也叫作p阶自回归模型。指的是通过这个时刻点的前p个点，通过线性组合再加上白噪声来预测当前时刻点的值。

AR是线性时间序列分析模型中最简单的模型，通过前面部分的数据与后面部分的数据之间的相关关系来建立回归方程：
AR§，表示p阶的自回归过程，为自回归系数，表示白噪声，是时间序列中的数值的随机波动。这些波动会相互抵消，即累计为0
如果只有一个时间记录点时，则为AR(1)，即一阶自回归过程：

4.2移动平均MA(Moving Average)

与AR模型大同小异，AR模型是历史时序值的线性组合，MA是通过历史白噪声进行线性组合来影响当前时刻点。

MA模型中的历史白噪声是通过影响历史时序值，从而间接影响到当前时刻点的预测值。
MA模型存在一个阶数q，称为MA(q)模型，也叫作q阶移动平均模型。AR和MA模型都存在阶数，在AR模型中，用p表示，在MA模型中用q表示，这两个模型大同小异，与AR模型不同的是MA模型是历史白噪声的线性组合。

MA模型，通过前面通过将一段时间序列中白噪声序列进行加权和，可以得到移动平均方程：

MA(q)表示q阶移动平均过程，为移动回归系数，为不同时间点的白噪声
Xt 为第t天的股票价格，而Ut为第t天的新闻影响，当天的股票价格受当天的新闻影响，也受昨天的新闻影响（但影响力要弱些，所以要乘上系数）

4.3ARMA 模型(Auto Regressive Moving Average)

AR模型和MA模型的混合，相比AR模型和MA模型，它有更准确的估计
ARMA模型存在p和q两个阶数，称为ARMA(p,q)模型：

自回归模型结合了两个模型的特点，AR解决当前数据与后期数据之间的关系，MA则可以解决随机变动，即噪声问题。

Auto Regressive Integrated Moving Average模型，中文叫差分自回归滑动平均模型，也叫求合自回归滑动平均模型。相比于ARMA，ARIMA多了一个差分的过程，作用是对不平稳数据进行差分平稳，在差分平稳后再进行建模。ARIMA的原理和ARMA模型一样。相比于ARMA(p,q)的两个阶数，ARIMA是一个三元组的阶数(p,d,q)，称为ARIMA(p,d,q)模型，其中d是差分阶数。AR，MA是ARMA的特殊形式，而ARMA是ARIMA的特殊形式。

ARIMA模型步骤：
Step1，观察时间序列数据，是否为平稳序列
Step2，对于非平稳时间序列要先进行d阶差分运算，化为平稳时间序列
Step3，使用ARIMA（p, d, q）模型进行训练拟合，找到最优的(p, d, q)，及训练好的模型
Step4，使用训练好的ARIMA模型进行预测，并对差分进行还原

ARIMA 用差分将不平稳数据先变得平稳，再用ARMA模型

4.3.1差分小知识

差分=序列之间做差值，目的是为了得到平稳的序列，也就是去掉前面数值的影响
一次差分为序列之间做一次差值，二次差分为在一次差分的基础上在做一次差分

若x=[1,4,9,16,25….]（x有二次趋势）

一次差分的结果为[4-1,9-4,16-9,25-16…] = [3,5,7,9,11…]，此时x序列仍不平稳，有一次上升的趋势
再做一次差分为[2,2,2,2…] ，此时x为平稳序列

5.时间序列实战

5.1statsmodels工具

statsmodels工具包提供统计计算，包括描述性统计以及统计模型的估计和推断

statsmodels主要包括如下子模块：
回归模型：线性回归，广义线性模型，线性混合效应模
方差分析（ANOVA）
时间序列分析：AR，ARMA，ARIMA等

import statsmodels.api as sm
# 数据加载
data = pd.read_csv('shanghai_index_1990_12_19_to_2019_12_11.csv', usecols=['Timestamp', 'Price'])
data.Timestamp = pd.to_datetime(data.Timestamp)
data = data.set_index('Timestamp')
data['Price'] = data['Price'].apply(pd.to_numeric, errors='ignore')
# 进行线性插补缺漏值
data.Price.interpolate(inplace=True)
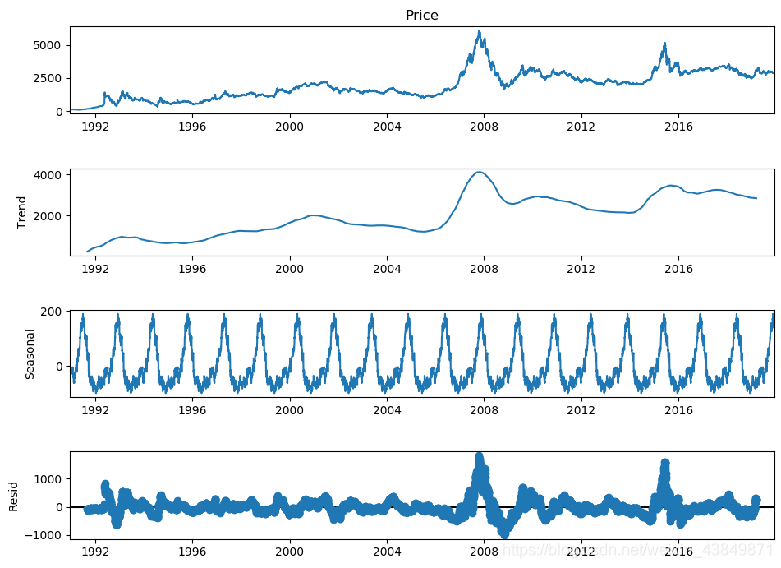
#  返回三个部分 trend（趋势），seasonal（季节性）和residual (残留)
result = sm.tsa.seasonal_decompose(data.Price, freq=288)
result.plot()
plt.show()

在这里插入图片描述

5.2时间序列分析与回归分析的区别

在选择模型前，我们需要确定结果与变量之间的关系。回归分析训练得到的是目标变量y与自变量x（一个或多个）的相关性，然后通过新的自变量x来预测目标变量y。而时间序列分析得到的是目标变量y与时间的相关性

在这里插入图片描述

回归分析擅长的是多变量与目标结果之间的分析，即便是单一变量，也往往与时间无关。而时间序列分析建立在时间变化的基础上，它会分析目标变量的趋势、周期、时期和不稳定因素等。这些趋势和周期都是在时间维度的基础上，是我们要观察的重要特征

5.3ARMA实战

# 从statsmodels导入ARMA
from statsmodels.tsa.arima_model import ARMA

ARMA(endog,order,exog=None)
endog：endogenous
variable，代表内生变量，又叫非政策性变量，它是由模型决定的，不被政策左右，可以说是我们想要分析的变量，或者说是我们这次项目中需要用到的变量
order：代表是p和q的值，也就是ARMA中的阶数
exog：exogenous
variables，代表外生变量。外生变量和内生变量一样是经济模型中的两个重要变量。相对于内生变量而言，外生变量又称作为政策性变量，在经济机制内受外部因素的影响，不是我们模型要研究的变量

如果我们想要创建ARMA(7,0)模型，可以写成：ARMA(data,(7,0))，其中data是我们想要观察的变量，(7,0)代表(p,q)的阶数。

fit函数，进行拟合
predict(start, end)函数，进行预测，其中start为预测的起始时间，end为预测的终止时间

# 用ARMA进行时间序列预测
from statsmodels.tsa.arima_model import ARMA
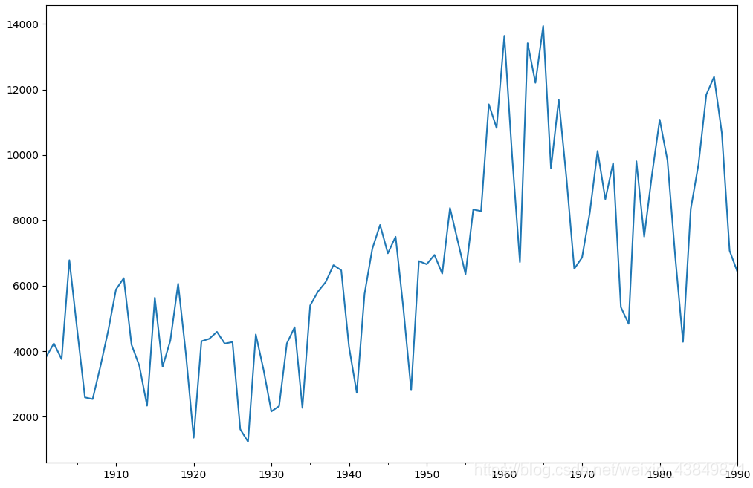
# 创建数据
data = [3821, 4236, 3758, 6783, 4664, 2589, 2538, 3542, 4626, 5886, 6233, 4199, 3561, 2335, 5636, 3524, 4327, 6064, 3912, 1356, 4305, 4379, 4592, 4233, 4281, 1613, 1233, 4514, 3431, 2159, 2322, 4239, 4733, 2268, 5397, 5821, 6115, 6631, 6474, 4134, 2728, 5753, 7130, 7860, 6991, 7499, 5301, 2808, 6755, 6658, 6944, 6372, 8380, 7366, 6352, 8333, 8281, 11548, 10823, 13642, 9973, 6723, 13416, 12205, 13942, 9590, 11693, 9276, 6519, 6863, 8237, 10122, 8646, 9749, 5346, 4836, 9806, 7502, 9387, 11078, 9832, 6886, 4285, 8351, 9725, 11844, 12387, 10666, 7072, 6429]
data=pd.Series(data)
data_index = sm.tsa.datetools.dates_from_range('1901','1990')

# 绘制数据图
data.index = pd.Index(data_index)
data.plot(figsize=(12,8))
plt.show()
# 创建ARMA模型# 创建ARMA模型
arma = ARMA(data,(7,0)).fit()
print('AIC: %0.4lf' %arma.aic)
# 模型预测
predict_y = arma.predict('1990', '2000')
# 预测结果绘制
fig, ax = plt.subplots(figsize=(12, 8))
ax = data.ix['1901':].plot(ax=ax)
predict_y.plot(ax=ax)
plt.show()

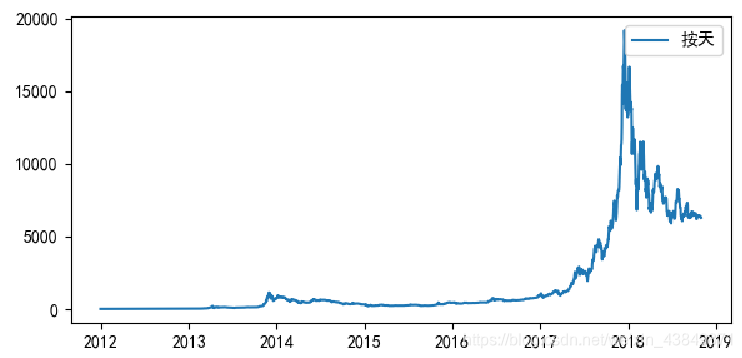
在这里插入图片描述

5.3.1ARMA工具对沪市指数进行预测

Step1，数据加载&探索
按照不同的时间尺度（天，月，季度，年）可以将数据压缩，得到不同尺度的数据，然后做可视化呈现。这4个时间尺度上，我们选择“月”作为预测模型的时间尺度

df_month = df.resample(‘M’).mean()

Step2，模型选择&训练，在给定范围内，选择最优的超参数
创建ARMA时间序列模型。我们并不知道p和q取什么值时，模型最优，因此可以给它们设置一个区间范围，比如都是range(0,3)，然后计算不同模型的AIC数值，选择最小的AIC数值对应的那个ARMA模型

Step3，模型预测，可视化呈现
用这个最优的ARMA模型预测未来3个月的沪市指数走势，并将结果做可视化呈现。
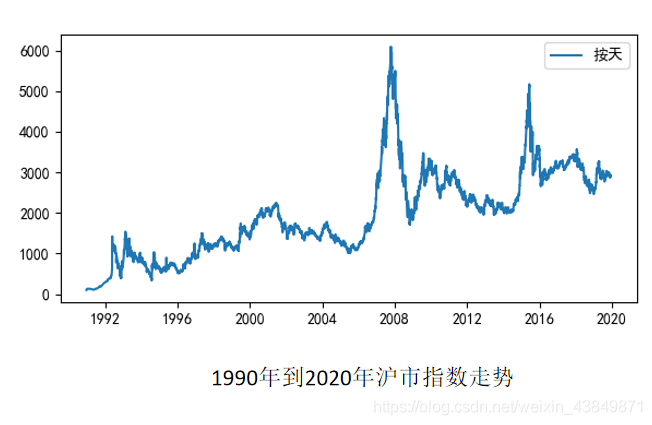
在这里插入图片描述

# 数据加载
df = pd.read_csv('shanghai_index_1990_12_19_to_2020_03_12.csv')
df = df[['Timestamp', 'Price']]
# 将时间作为df的索引
df.Timestamp = pd.to_datetime(df.Timestamp)
df.index = df.Timestamp
# 数据探索
print(df.head())
# 按照月，季度，年来统计
df_month = df.resample('M').mean()
print(df_month)
df_Q = df.resample('Q-DEC').mean()
df_year = df.resample('A-DEC').mean()

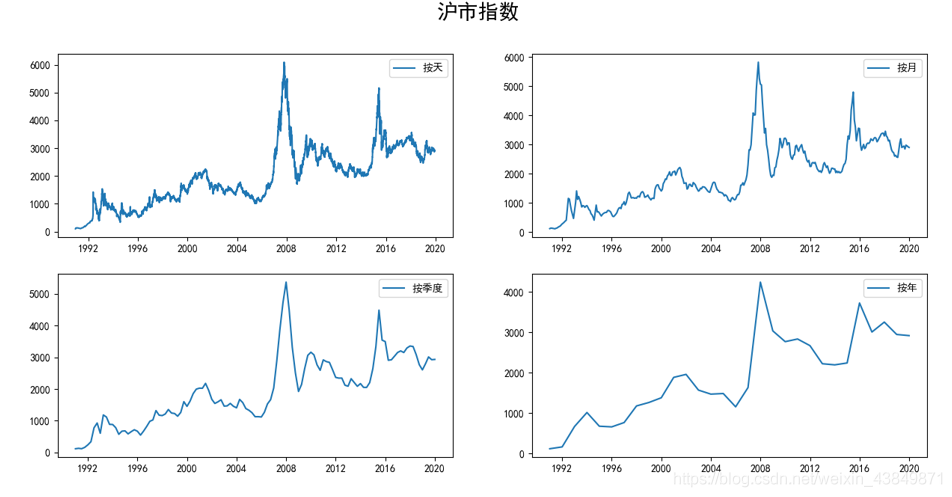
# 按照天，月，季度，年来显示沪市指数的走势
fig = plt.figure(figsize=[15, 7])
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.suptitle('沪市指数', fontsize=20)
plt.subplot(221)
plt.plot(df.Price, '-', label='按天')
plt.legend()
plt.subplot(222)
plt.plot(df_month.Price, '-', label='按月')
plt.plot(df_Q.Price, '-', label='按季度')
plt.plot(df_year.Price, '-', label='按年')
plt.legend()
plt.show()

在这里插入图片描述

# 设置参数范围
ps = range(0, 3)
qs = range(0, 3)
parameters = product(ps, qs)
parameters_list = list(parameters)
# 寻找最优ARMA模型参数，即best_aic最小
results = []
best_aic = float("inf") # 正无穷
for param in parameters_list:
    try:
        model = ARMA(df_month.Price,order=(param[0], param[1])).fit()
    except ValueError:
        print('参数错误:', param)
        continue
    aic = model.aic
    if aic < best_aic:
        best_model = model
        best_aic = aic
        best_param = param
    results.append([param, model.aic])
print('最优模型: ', best_model.summary())

在这里插入图片描述

# 设置future_month，需要预测的时间date_list
future_month = 3
last_month = pd.to_datetime(df_month2.index[len(df_month2)-1])
date_list = []
for i in range(future_month):
    # 计算下个月有多少天
    year = last_month.year
    month = last_month.month
    if month == 12:
        month = 1
        year = year+1
    else:
        month = month + 1
    next_month_days = calendar.monthrange(year, month)[1]
    #print(next_month_days)
    last_month = last_month + timedelta(days=next_month_days)
    date_list.append(last_month)
print('date_list=', date_list)

date_list= [Timestamp('2020-04-30 00:00:00', freq='M'), Timestamp('2020-05-31 00:00:00', freq='M'), Timestamp('2020-06-30 00:00:00', freq='M')]

# 添加未来要预测的3个月
future = pd.DataFrame(index=date_list, columns= df_month.columns)
df_month2 = pd.concat([df_month2, future])
df_month2['forecast'] = best_model.predict(start=0, end=len(df_month2))
# 第一个元素不正确，设置为NaN
df_month2['forecast'][0] = np.NaN
print(df_month2)
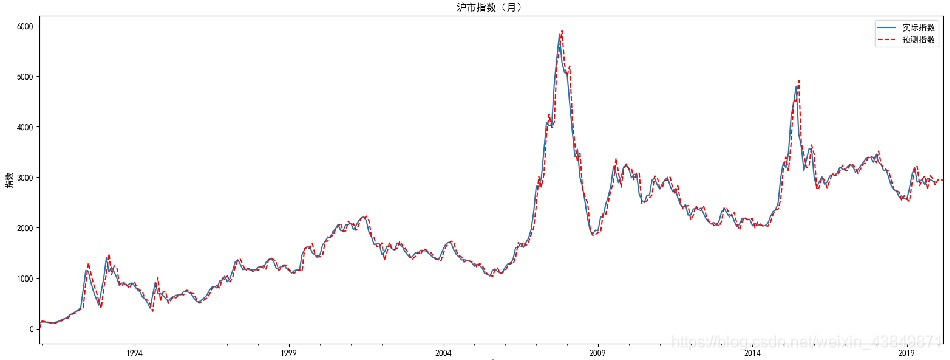
# 沪市指数预测结果显示
plt.figure(figsize=(30,7))
df_month2.Price.plot(label='实际指数')
df_month2.forecast.plot(color='r', ls='--', label='预测指数')
plt.legend()
plt.title('沪市指数（月）')
plt.xlabel('时间')
plt.ylabel('指数')
plt.show()

在这里插入图片描述

5.4使用LSTM进行时间序列预测

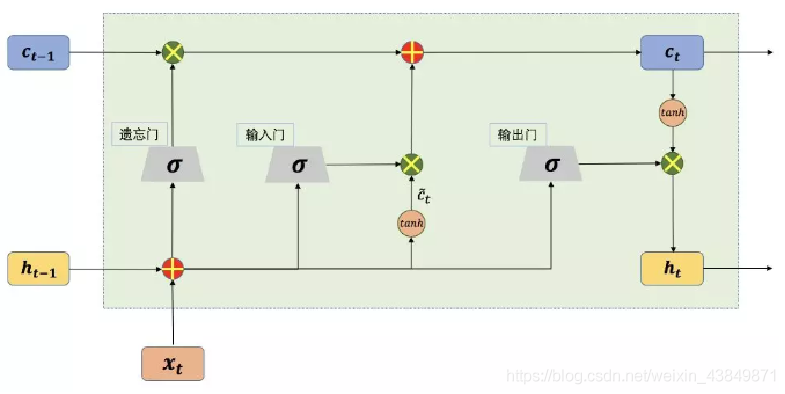
LSTM，Long Short-Term Memory，长短记忆网络
可以避免常规RNN的梯度消失，在工业界有广泛应用
引入了三个门函数：输入门（Input Gate）、遗忘门（Forget Gate）和输出门（Output Gate）来控制输入值、记忆值和输出值
输入门决定了当前时刻网络的状态有多少信息需要保存到内部状态中，遗忘门决定了过去的状态信息有多少需要丢弃 => 输入门和遗忘门是LSTM能够记忆长期依赖的关键
输出门决定当前时刻的内部状态有多少信息需要输出给外部状态。
在这里插入图片描述
一个LSTM单元在每个时间步会接收三个输入：