The PageRank Citation Ranking Bringing Order to the Web（1997 谷歌搜索引擎算法）以及用PageRank计算四大名著人物重要性及关系代码_the pagerank citation ranking: bringing order to t-CSDN博客

本文链接：https://blog.csdn.net/weixin_43856668/article/details/134576960

The PageRank Citation Ranking Bringing Order to the Web----《PageRank引用排名：给互联网带来秩序》

PageRank将互联网表示成了图（有向图），节点为网络，边为引用关系。

节点重要性排序算法：一个网页的重要性以其入度衡量，不同入度边的权重不同，需要根据引用该网页的其他网页的重要性（递归问题）。

理解 PageRank 的五个角度：

① 迭代求解线性方程（ $O({n^3})$ ）

在这里插入图片描述

$r_j^{(t + 1)} = \sum\limits_{i \to j} {\frac{{r_i^{(t)}}}{{{d_i}}}}$ ，其中， ${{d_i}}$ 是节点 $i$ 的出度数量。

注：重要节点引出的稀少链接，权重更高。

举例：

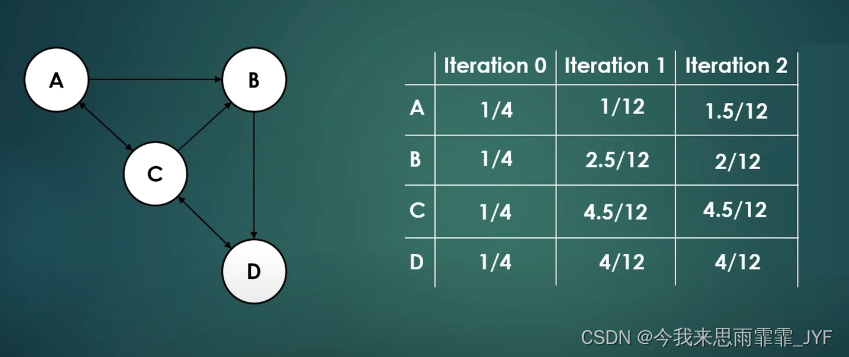
在这里插入图片描述

② 迭代左乘 $M$ 矩阵（ $M$ 矩阵每列求和为1，if $\to j,{M_{ji}} = \frac{1}{{{d_i}}}$ ）

幂迭代运算： $... M (M (M (r)))$

在这里插入图片描述

③ 矩阵的特征向量（ $O({n^3})$ ）

$\cdot {r^1} = M \cdot {r^0}$ （即特征值为1的特征向量）

其中，1是特征值， ${\vec r^0}$ 是 $M$ 矩阵的特征向量。

④ 随机游走

$\cdot p(t) = p(t)$ （稳定收敛分布）

其中， $\cdot )$ 表示访问概率。

⑤ 马尔科夫链（状态和状态之间的转移）

类似随机游走

PageRank 算法步骤：

初始化： ${r^{(0)}} = {[1/N,...,1/N]^T}$

迭代： ${r^{(t + 1)}} = M \cdot {r^{(t)}} \Leftrightarrow {r_j}^{(t + 1)}\sum\limits_{i \to j} {\frac{{r_i^{(t)}}}{{{d_i}}}}$

迭代收敛（结束）条件： $\sum\nolimits_i {{{\left| {{r^{(t + 1)}} - {r^{(t)}}} \right|}_1} < \varepsilon }$

存在问题：

① 爬虫：仅指向自己
在这里插入图片描述
② 死胡同节点

解决方案： $\beta \%$ 的概率按原路线随机游走， $\beta )\%$ 的概率被随机传送到其他节点，死胡同节点100%被传送走（即 M 矩阵中该节点的列为 0）。

${r_j} = \sum\limits_{i \to j} {\beta \frac{{{r_i}}}{{{d_i}}} + (1 - \beta )} \frac{1}{N}$

谷歌矩阵：

$\beta M + (1 - \beta ){[\frac{1}{N}]_{N \times N}}$

$\cdot r$

代码：四大名著人物重要性及关系

数据集下载地址：http://openkg.cn/dataset/ch4masterpieces

import networkx as nx  # 图数据挖掘包
import numpy as np  # 数据分析
import random
import pandas as pd

# 数据可视化
import matplotlib.pyplot as plt
import matplotlib as mpl
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# 导入数据集
df = pd.read_csv('./data/西游记/triples.csv')
# df = pd.read_csv('./data/红楼梦/triples.csv')
# df = pd.read_csv('./data/三国演义/triples.csv')
# df = pd.read_csv('./data/水浒传/triples.csv')
# 图的边
edges = [edge for edge in zip(df['head'], df['tail'])]
# 建图
G = nx.DiGraph()
# 添加边
G.add_edges_from(edges)
# print(G)
pos = nx.spring_layout(G, iterations=3, seed=5)
# 可视化
'''
plt.figure(figsize=(15, 14))
nx.draw(G, pos, with_labels=True)
plt.show()
'''
# 计算每个节点pagerank重要度
pagerank = nx.pagerank(
    G,
    alpha=0.85,
    personalization=None,
    max_iter=100,
    tol=1e-06,
    nstart=None,
    dangling=None,
)
# print(pagerank)
# 从高到低排序
# pagerank = sorted(pagerank.items(), key=lambda x: x[1], reverse=True)
# print(pagerank)
# 节点尺寸
node_sizes = (np.array(list(pagerank.values())) * 8000).astype(int)
# 节点颜色
M = G.number_of_edges()
edge_colors = range(2, M + 2)
plt.figure(figsize=(15, 14))
# 绘制节点
nodes = nx.draw_networkx_nodes(G, pos, node_size=node_sizes, node_color=node_sizes)
# 绘制连接
edges = nx.draw_networkx_edges(
    G,
    pos,
    node_size=node_sizes,
    arrowstyle="->",
    arrowsize=20,
    edge_color=edge_colors,  # 连接颜色
    edge_cmap=plt.cm.plasma,  # 连接配色方案
    width=2  # 连接线宽
)
# 设置每个连接的透明度
edge_alphas = [(5 + i) / (M + 4) for i in range(M)]
for i in range(M):
    edges[i].set_alpha(edge_alphas[i])
ax = plt.gca()
ax.set_axis_off()
plt.show()

效果显示：

西游记：
在这里插入图片描述 红楼梦：

三国演义：

水浒传：

参考资料：
Page L. The pagerank citation ranking: Bringing order to the web. Technical report[J]. Stanford Digital Library Technologies Project, 1998, 1998.

https://www.bilibili.com/video/BV1uP411K7yN/?spm_id_from=333.337.top_right_bar_window_history.content.click&vd_source=7cd832849e4c246304cfbcad8b79ff7a