拓扑排序（DFS和BFS及判断是否有环）

最新推荐文章于 2023-12-04 08:54:06 发布

‘’云腾致雨‘’

最新推荐文章于 2023-12-04 08:54:06 发布

阅读量5.2k

点赞数 4

分类专栏：拓扑排序

本文链接：https://blog.csdn.net/weixin_43918531/article/details/86740991

版权

拓扑排序通过解决谁先谁后的问题，实现有向无环图的排序。本文探讨了使用DFS和BFS两种方法进行拓扑排序，并详细解释了在无环和有环情况下如何进行操作。对于DFS，通过递归处理有向边，判断有环时增加状态标识。而BFS则从入度为0的节点开始，逐步减少相邻节点的入度，以此判断有环情况。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

拓扑排序其实还是挺奇妙的，就是解决谁先谁后的问题，~~solve contradictions and make the world peaceful~~接下来就探讨一下拓扑排序的两种实现方法。

一（DFS）：

1.（无环）

我们给定一个有向无环图：
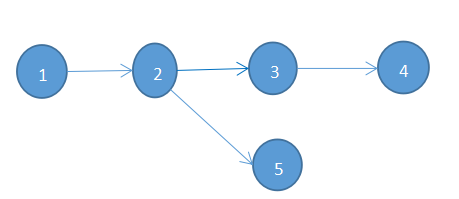
在这里插入图片描述
DFS是从一个点不断往下递归，比如说从序号1往下递归，有箭头就一直往下进行，直到到了最后一个元素，就开始往栈里（当然也可以是vector之类的，只不过需要反向再输出）push元素。比如说上面的从序号1开始，到序号2，序号3，序号4，到尽头了，就把4push进栈中，3push进栈，这个时候由于5也是2的下一个元素，所以5push进栈中，2push进栈，1push进栈，然后输出就是1 2 5 3 4.
当然这个递归的顺序是与你输入的顺序有关的，不过思路都是这样的，由起始点向下递归。
所以说dfs的代码还是比较简单的：

#include <bits/stdc++.h> 
const int inf=0x3f3f3f3f;
using namespace std;
bool vis[1001];
vector<int>G[1002];   //邻接表
vector<int>ans;
void dfs(int x)
{
   
    int i,v;
    vis[x]=1;
    for(i=0;i<G[x].size();i++)
    {
   
        v=G[x][i];
        if(!vis[v])
        {
   
            vis[v]=1;
            dfs(v);
        }
    }
    ans.push_back(x);             //这一层完毕才把它自己扔进去。
}
int main()
{
   
    int n,m,i,A,B;
    cin>>n>>

最低0.47元/天解锁文章