局部加权线性回归 实现

局部加权线性回归

依赖

import numpy as np
import matplotlib.pyplot as plt

人工数据集

n = 100
true_theta1 = np.array([1, 2]).reshape(-1,1)
true_theta2 = np.array([16, -3]).reshape(-1,1)

X = np.random.normal(3, 1, (n,1))
X = np.insert(X, 0, 1, axis = 1)

def get_y(X):
    return np.array([e @ true_theta2 if e[1]>3 else e @ true_theta1  for e in X]).reshape(-1,1)

y = get_y(X) + np.random.normal(0, 0.01, (n,1))
np.insert(X, 2, y.T, axis = 1)
plt.scatter(X[:,1], y)

<matplotlib.collections.PathCollection at 0x7efdca896fd0>

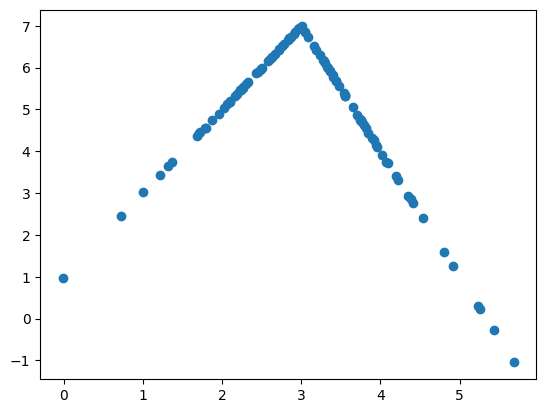
以上为人工数据集分布。

局部加权线性回归函数

本代码通过使用最小二乘法直接求最优解。

def lwlr(X, x, y, k):#直接返回最优解的theta
    m = X.shape[0]
    W = np.diag(np.exp(-(X[:,1]-x)**2/2/(k**2)))
    return np.linalg.pinv(X.T @ W @ X) @ X.T @ W @ y

#np.array([1,x]) @ theta ,np.array([1,x]) @ true_theta1, np.array([1,x]) @ true_theta2, get_y([[1,x]])

损失函数

损失函数如下，其中$w_i=e^{\frac{(x-x_i{)}^2}{2{\tau }^2}}$

$$\begin{array}{rcl}J(\theta \theta )& =& \frac{1}{n}{\sum }_{i=1}^n{w}_i({XX}_i\theta \theta -y_i{)}^2\\ & =& (XX\theta \theta -yy{)}^{T}WW(XX\theta \theta -yy)\end{array}$$
对表达式求导：
$$\begin{array}{rcl}\frac{\partial J(\theta \theta )}{\partial \theta \theta }& =& {\nabla }_{\theta \theta }((XX\theta \theta -yy{)}^{T}WW(XX\theta \theta -yy))\\ & \stackrel{xx=XX\theta \theta -yy}{=}& \frac{\partial {xx}^{T}WWxx}{\partial xx}{\nabla }_{\theta \theta }(XX\theta \theta -yy)\\ & =& (2WWxx{)}^{T}XX\\ & =& 2(XX\theta \theta -yy{)}^{T}WWXX\end{array}$$

令$\frac{\partial J(\theta \theta )}{\partial \theta \theta }=00$
得$2(XX\theta \theta -yy{)}^{T}WWXX=00$
$$\begin{array}{rcl}2(XX\theta \theta -yy{)}^{T}WWXX& =& 00\\ (XX\theta \theta -yy{)}^{T}WWXX& =& 00\\ ((XX\theta \theta {)}^T-{yy}^T)WWXX& =& 00\\ ({\theta \theta }^T{XX}^T-{yy}^T)WWXX& =& 00\\ {\theta \theta }^T{XX}^{T}WWXX-{yy}^{T}WWXX& =& 00\\ {\theta \theta }^T{XX}^{T}WWXX& =& {yy}^{T}WWXX\\ {XX}^{T}WWXX\theta \theta & =& {XX}^{T}WWyy\\ \theta \theta & =& ({XX}^{T}WWXX{)}^{-1}{XX}^{T}WWyy\end{array}$$

预测

k=1
xrange = [x for x in np.arange(-1,10,0.1)] 
t1 = [get_y([[1,x]])[0][0] for x in xrange]
print(t1)
#print(xrange)
#print([x for x in xrange])
t2 = [(np.array([[1,x]])@ lwlr(X, x, y, k))[0][0] for x in xrange]
print(t2)
c = ['o' for x in xrange] + ['+' for x in xrange]
for xx, yy, cc in zip([xrange[:],xrange[:]],[t1[:],t2[:]], c):
    plt.scatter(xx, yy, marker = cc)
for i in xrange:
    print(f"当x点为{i},真实值为{get_y([[1, i]])}，预测值为{np.array([[1, i]])@ lwlr(X, i, y, k)}")
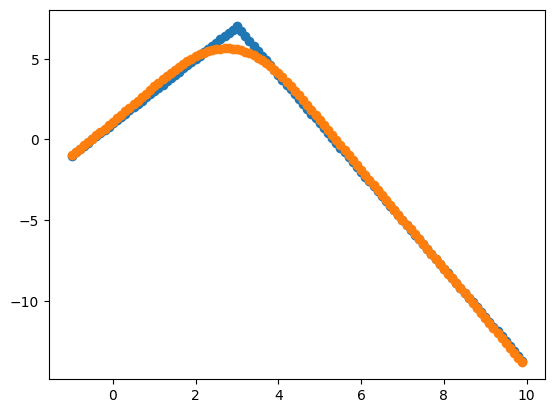
plt.show()

!

(●’◡’●)

局部加权线性回归需要保存训练的数据，能拟合不能确定模糊表达式的点集，其预测值主要会被附近的点影响，但远离预测值$x$的对预测值的影响几乎为零。通过$w$函数实现一个类钟形曲线的权重。当超参数$\tau$(代码里的k)的大小能够调节钟形曲线的瘦高还是矮胖。$\tau$越小，会更符合原数据，也会容易过拟合。而$\tau$越大，曲线将会受很远的值影响，也会能预测出数据较少或者的位置的值。

但我所构建的数据集，其实并不符合实际，生活中的数据不应该出现毛刺，应该更平滑点如预测曲线，所以我认为预测曲线更符合实际。