回溯算法套路①子集型回溯 - 灵神视频总结

养那个乐多

已于 2024-07-05 01:20:54 修改

阅读量2.3k

点赞数 49

分类专栏：算法刷题文章标签：算法数据结构

于 2024-07-05 01:20:01 首次发布

本文链接：https://blog.csdn.net/weixin_43939296/article/details/140193979

版权

算法刷题专栏收录该内容

13 篇文章

订阅专栏

我回来了，前两天模型出了问题，忙于工作。

加上回溯有点想不清楚，查了查资料。汗颜。

这节课主要讲回溯的基本概念和回溯的基本套路。

首先各位思考一个问题：如果生成一个长度为2的字符串，该怎么操作？

我们通常的想法是用两层循环拼接就好，如果用两层循环，如果我要生成长为2或者3的，甚至长度不固定的该怎么写的呢？无能为力，单纯的递归表达能力有限。

那该如何思考呢？

之前在前面讲过递归的概念，那么原问题是构造长为n的字符串，那么子问题就是构造长为n-1的字符串。那么构造长为n的字符串，在枚举了一个字符串之后，就变成构造长为n-1的字符串。这种从原问题到子问题的过程适合用递归解决。通过递归可以达到多重递归的效果。

回溯和递归有什么关系呢？

像这种题目，比如构建长度为2的字符串，有个增量构造答案的过程，这个过程通常可以使用递归来解决。

那回忆一下递归，我们不需要想很多，只需要想明白边界条件和非边界条件逻辑即可，其他的交给数学归纳法。

这里有个模版，思考问题的套路

当前操作，就是枚举一个字母。dfs(i) i 不是枚举的字母i，而是第>=i 的部分。用一个全局变量来记录结果。

好，我们看一道题

17. 电话号码的字母组合

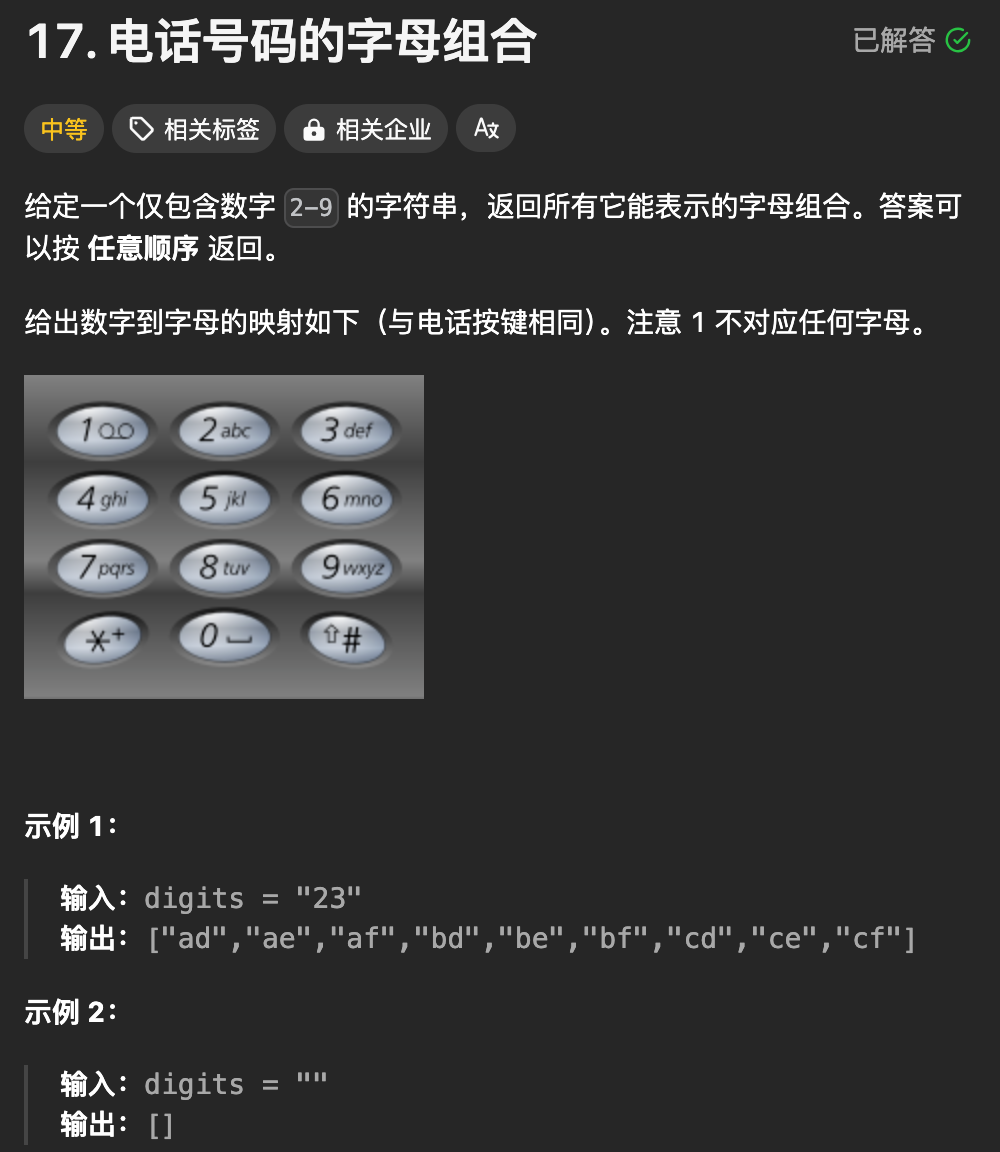
就按照刚才讲的逻辑写一下代码，如果不懂，可以看注释。

MAPPING = ["", "", "abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"] # {1:"abc"}
class Solution:
    def letterCombinations(self, digits):
        # 时间复杂度O(n*4^n)
        n = len(digits)
        if n == 0 :
            return []
        ans = []
        path = ['']*n
        def dfs(i): # 从i开始，构造到n个字符串。
            if i == n: #边界条件，当等于n时，构建完了，需要结束了。
                ans.append("".join(path)) # 把结果放进去。
                return
            for c in MAPPING[int(digits[i])]: # 可以想两层，先拿第一个字母，
                path[i] = c 
                dfs(i+1) # 从i+1开始，构造到n个字符串。
        dfs(0) # 从第0个数字开始递归。
        return ans 
    
so = Solution()
print(so.letterCombinations("29"))

分析下时间复杂度，可以从循环的角度理解，循环次数最多循环4^n次方，存储答案还需要n，时间复杂度为O(n*4^n)

回溯的套路

这里讲子集型回溯。

问题：计算[1,2]的所有子集。

每个元素都可以选或者不选，就有4中选择，1 选/不选 2 选/不选

要想生成所有子集，有两种操作，区别在于当前的操作是什么？

代码 - 看注释

当前操作是选/不选当前元素。

子问题是 -> 从大于等于i个元素开始选

下一个子问题就是已经对当前做出了选择，然后递归下标 i + 1 个元素。

这就是递归，不要想太多，只关注当前问题和当前问题和下个问题的逻辑条件，其他的交给数学归纳法。

要相信数学归纳法。

看代码

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        ans = []
        path = []
        def dfs(i): # 选不选i
            if i == n:
                ans.append(path.copy()) #why？
                return 
            dfs(i+1)

            path.append(nums[i])
            dfs(i+1)
            path.pop() # 为什么要恢复现场？
        dfs(0)
        return ans

针对代码再啰嗦两句：

首先它是递归，递归就是写边界条件和非边界条件，其他的交给数学归纳法。
要明白或者清楚你在递归什么。即递归的东西是什么，里面的参数是什么，这个就是要想清楚子问题是什么。

细节：为什么要加入path.copy() ,
如果直接将 path 添加到 ans 中，而不使用 path.copy()，那么 path 在后续的 dfs 中被修改时，已经添加到 ans 中的 path 也会被修改，这会导致答案错误。
使用 path.copy() 复制一份 path，可以确保每个子集都是独立的，不会相互影响。这样就可以正确地构建出所有的子集，避免出现错误。

为什么会要恢复现场？

在递归到某一“叶子节点”（非最后一个叶子）时，答案需要向上返回，而此时还有其他的子树（与前述节点不在同一子树）未被递归到，又由于path为全局变量。若直接返回，会将本不属于该子树的答案带上去，故需要恢复现场。
恢复现场的方式为：在递归完成后 dfs(i+1); 后，进行与“当前操作”相反的操作，“反当前操作”。

这题还有第二种解法

这里解释什么是答案的角度？就是第一个数选谁，第二个数选谁。

就固定一个遍历的顺序就行。

当前操作：枚举下一个j>= i 的数字。

子问题就需要从下表 >=j +1 的数字中构建子集。

class Solution:
    def subsets(self, nums: List[int]) -> List[List[int]]:
        n = len(nums)
        if n == 0 :
            return []

        path = []
        ans = []
        def dfs(i):
            ans.append(path.copy())
            if i == n:
                return 
            for j in range(i, n):
                path.append(nums[j])
                dfs(j+1)
                path.pop()
        dfs(0)
        return ans

枚举逗号的位置。

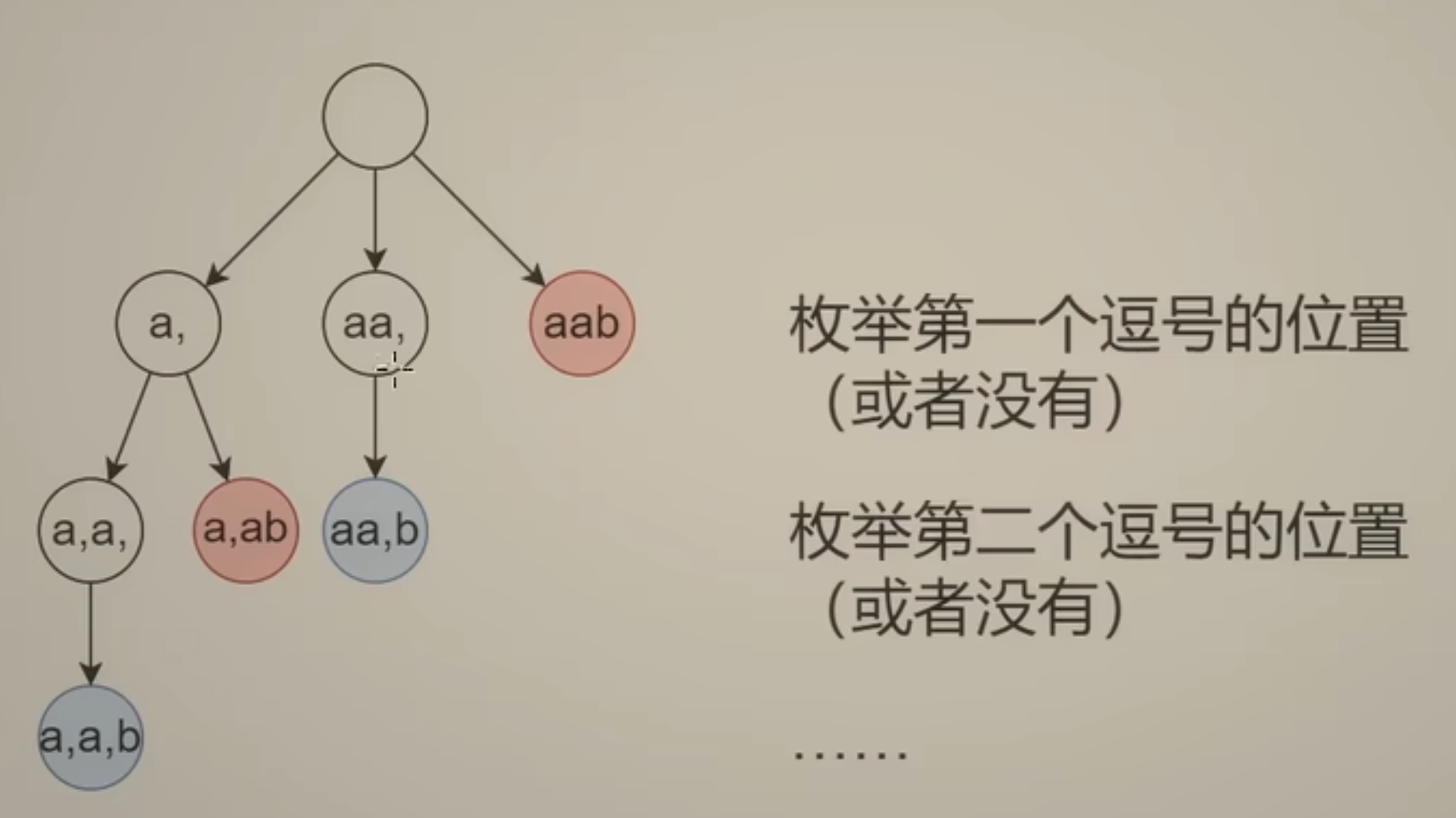
回文子串怎么弄？相向双指针

看代码：

class Solution:
    def partition(self, s: str) -> List[List[str]]:
        n = len(s)
        if n == 0:
            return []

        ans = []
        path = []
        def dfs(i): # 枚举逗号的位置。
            if i == n:
                ans.append(path.copy()) #复制path
                return 
            for j in range(i, n): #枚举子串的结束位置。
                t = s[i: j+1]
                if t == t[::-1]:
                    path.append(t)
                    dfs(j+1)
                    path.pop() #恢复现场。
        dfs(0)
        return ans