动态规划-（0-1背包问题）

前言

最近在做动态规划的练习时遇到了0-1背包问题，当时困扰了很久，在反复思考以及与人讨论和学习后，有了一些自己的理解，在这里将这类问题的思路整理一下。

0-1背包问题

这是在百度百科找到的背包问题的解释


简单来说，该问题就是：给定n种物品和一背包。物品 i 的重量为 w[i]，其价值为 v[i]，背包的容量为 c。问应该如何选择装入背包中的物品，使得装入背包中物品的总价值最大？

思路分析

我们总是用专业术语来讨论问题很容易把自己绕进去，而且容易思路混乱，理解乏力。那么我们就用一些简单易懂的例子来解释这个问题
假如你最近生活遇到了一些困难，手头上没有钱，你今天想要用一个可以背4公斤的包，背着几件物品出去换取一定的钱来支持你最近的生活，价值自然越高越好。
可以让你挑选的东西有：

1. PS5主机/4kg/4000元
2. 二手笔记本电脑/3kg/3000元
3. 键盘/1kg/1500元

此时我们就有一种最简单直接的思路：
将所有的组合全都尝试一遍，将能形成组合的搭配在一起，不能形成组合的舍弃，再比较组合中哪一个价值最高，取价值最高的那个

1. 无：0元、0kg（√）
2. PS5主机： 4000元、4kg（√）
3. 二手笔记本电脑： 3000元、3kg（√）
4. 键盘： 1500元、1kg（√）
5. PS5主机+二手笔记本电脑： 7000元、7kg（×）
6. PS5主机+键盘：5500元、5kg（×）
7. 二手笔记本电脑+键盘： 4500元、4kg（√）
8. PS5主机+二手笔记本电脑+键盘：8500元、8kg（×）

只有三种物品，我们却要列出总共8种组合，如果我们再加一种物品，就会高达16种组合，整个运算过程时间复杂度达到了O(2ⁿ)，真是太浪费时间了。

动态规划解决

既然我们使用简单的思路会导致时间复杂度太大，那么我们就换一个思路试一试。通过动态规划，我们将主问题分解成若干个子问题，我们先解决了子问题，再去逐步解决主问题。
那么在这个问题中，我们可以分解的问题是什么？
背包容量！
开始给定了一个固定的背包容量，和几个重量为正整数的物品。我们将一个大的背包分解成若干个小背包，通过比较在单个小背包中可以装下的最大价值的物品，来确定最后在整个背包中可以装下的最大价值的物品。
我们可以用一个表格来表示这样的一个关系：

商品\容量	1	2	3	4
键盘
PS5主机
二手笔记本电脑

每一行代表着在当前重量下能不能放当前物品，放进去之后整个背包中物品的价值
比如第一个单元格，表示1kg的小背包中你能将键盘放进去，放入键盘后，价值为1500

商品\容量	1	2	3	4
键盘	1500
PS5主机
二手笔记本电脑

以此类推，第一行只能将键盘放入

商品\容量	1	2	3	4
键盘	1500	1500	1500	1500
PS5主机
二手笔记本电脑

但是到了第二行，开始复杂了起来，我们多了一个选项——二手笔记本电脑
在只能装1kg、2kg和3kg的小背包中，我们现在只能放下一个键盘，背包中的价值是不变的

商品\容量	1	2	3	4
键盘	1500	1500	1500	1500
PS5主机	1500	1500	1500
二手笔记本电脑

但是到了4kg的背包时，我们知道，PS5主机价值4000元，价值高于键盘，那么我们应该将该背包中的物品替换为价值更高的PS5主机

商品\容量	1	2	3	4
键盘	1500	1500	1500	1500
PS5主机	1500	1500	1500	4000
二手笔记本电脑

我们继续往下看
在1kg和2kg的背包中，我们只能放下键盘，所以第三行开始我们也只能填充价值1500的键盘

商品\容量	1	2	3	4
键盘	1500	1500	1500	1500
PS5主机	1500	1500	1500	4000
二手笔记本电脑	1500	1500

到了3kg的背包时，我们有了新的选择——二手笔记本电脑，价值为3000元，高于键盘，我们将键盘替换为二手笔记本电脑

商品\容量	1	2	3	4
键盘	1500	1500	1500	1500
PS5主机	1500	1500	1500	4000
二手笔记本电脑	1500	1500	3000

终于我们来到了最后一个背包——4kg的最终背包，这里的价值决定了我们最后能装下的最大价值
此时我们可以放入的选择有两种

1. PS5主机：价值4000元（上一个同等重量背包中物品的价值）
2. 键盘+二手笔记本电脑：价值4500元（当前物品的价值+剩余空间能放下的最大价值的物品的价值）

显然，第二个选择更符合我们的最大价值的题目要求，所以最后我们得到的表格如下：

商品\容量	1	2	3	4
键盘	1500	1500	1500	1500
PS5主机	1500	1500	1500	4000
二手笔记本电脑	1500	1500	3000	4500

状态转移方程

所以我们是如何来比较得出到底要选择哪一种组合的价值来填充当前的单元格呢？
我们把第一行和第一列的文字部分去掉，将这个表格当成一个二维数组来看，我们再来求其状态转移方程：
我们先将这个方程文字描述一遍：
当前背包中最大价值=以下两种组合中较大的一个
（1）上一个同等重量背包中物品的价值
（2）当前物品的价值+剩余空间能放下的最大价值的物品的价值
那么我们怎么用方程来表示呢？

value[i][j]=Math.max(value[i-1][j],value[i][j-1]+value[i-1][j-w]);

注：上述代码中value表示当前单元格能放下的最大价值，i对应当前的物品，j对应当前背包，w对应当前物品的重量

完整代码

有了以上的分析，我们就可以写出背包问题的代码了

public class KnapsackProblem {

    public int MaximumValue(int c ,int[] v ,int[] w){
        int n = v.length;//物品的个数为n
        int[][] form = new int[n][c];//创建一个表格行为物品个数，列为背包容量
        for (int i = 0; i < n; i++) {//置空表
            for (int j = 0; j < c; j++) {
                form[i][j] = 0;
            }
        }
        for (int i = 0; i < n; i++) {
            for (int j = 1; j <= c; j++) {
                if (i == 0) {//确定第一行的价值
                    form[i][j -1] = (w[i] <= j ? v[i] : 0);
                } else {
                    int last = form[i - 1][j - 1];  // 上一个同等重量的背包对应的价值
                    int now = (w[i] <= j ?       //重量是否符合
                                    (j - w[i] > 0 ? //容量是否有空余
                                        v[i] + form[i - 1][j - w[i]-1] // 若有空余，背包价值=当前物品的价值 + 剩余空间的价值
                                            : v[i])//若没有空余，等于当前物品价值
                            : last);//若不符合，价值等于上一个同等重量背包的价值（之前求得的最大价值）

                    // 返回两个值中较大的一个
                    form[i][j - 1] = (Math.max(last, now));
                }
            }
        }
        // 打印结果二维数组
        System.out.println("二维数组：");
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < c; j++) {
                System.out.printf("%6d", form[i][j]);
            }
            System.out.println();
        }
        return form[n-1][c-1];//返回最大价值
    }

    public static void main(String[] args) {
        KnapsackProblem knapsackProblem = new KnapsackProblem();
        int[] v = {1500, 4000, 3000};
        int[] w = {1, 4, 3};
        int c = 4;
        System.out.println("背包中物品的最大价值为："+knapsackProblem.MaximumValue(c, v, w));
    }
}

测试结果：

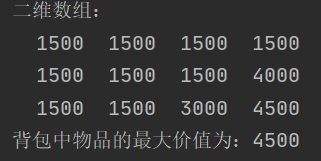
结果符合我们的问题分析

结语

学习动态规划的过程是很漫长的，当你解决了一个问题以为掌握了动态规划算法的时候，可能会出现一个新的问题开始困扰你，只有反复解决新的问题，勤加练习，多多思考，多向他人请教，才能有更多收获。