L1、L2正则化与贝叶斯先验分布的关系

最新推荐文章于 2024-03-23 20:15:53 发布

codestorm04

最新推荐文章于 2024-03-23 20:15:53 发布

阅读量2.9k

点赞数 1

分类专栏： Machine Learning Theory

Machine Learning Theory 专栏收录该内容

17 篇文章 1 订阅

订阅专栏

转自：https://note.youdao.com/ynoteshare1/index.html?id=2851b97199bcdc174001d72b1bec0372&type=note

（1）频率学观点：认为参数w是固定的，数据集D有多个，所以要解决的问题是什么样的w能使当前的D出现的可能性最大

假设给定输入x，其对应的label是t，且t服从高斯分布且均值为f(x)=wx+b
那么估计参数w的方法就是最大化w的似然函数 => 转化为最小化对数似然函数问题，得到 L = ½(f(x)-t)^2

（2）贝叶斯观点：认为D是固定的，参数w的不确定性由w的概率分布表达

即 P(w|D) 正比于 P(D|w)*P(w)
通过最小化对数似然函数，得到带正则项的loss

作者：Charles Xiao

链接：https://www.zhihu.com/question/23536142/answer/90135994

来源：知乎

著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

从贝叶斯的角度来看，正则化等价于对模型参数引入先验分布。

一. Linear Regression

我们先看下最原始的Linear Regression:

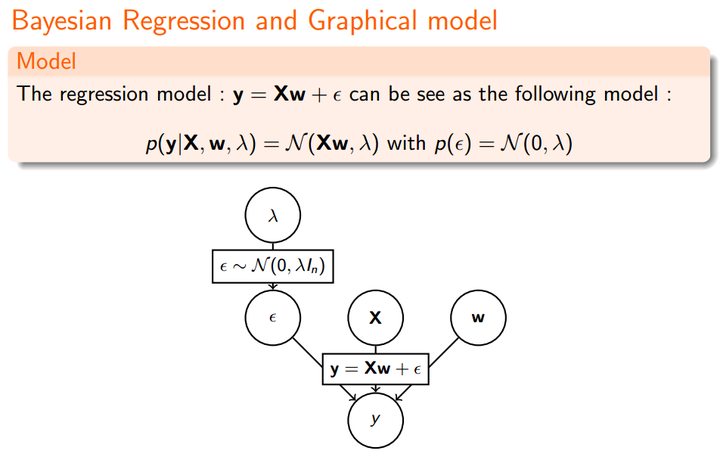
$\begin{align*} & p(\epsilon^{(i)}) = \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(\epsilon^{(i)})^2}{2\delta^2} \right)\\ \Rightarrow & p(y^{(i)}|x^{(i)};\theta) = \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right) \end{align*}$

由最大似然估计(MLE):

$\begin{align*} L(w) & = p(\vec{y}|X;w)\\ & = \prod_{i=1}^{m} p(y^{(i)}|x^{(i)};\theta)\\ & = \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right) \end{align*}$

取对数：

$\begin{align*} l(w) & = \log L(w)\\ & =\log \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})}{2\delta^2} \right)\\ & = \sum_{i=1}^{m} \log \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right)\\ & = m \log \frac{1}{\sqrt{2\pi}\delta} - \frac{1}{\delta^2}\cdot \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2 \end{align*}$

即：

$w_{MLE} = \arg \underset{w}{\min} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2$

这就导出了我们原始的 least-squares 损失函数，但这是在我们对参数 w 没有加入任何先验分布的情况下。在数据维度很高的情况下，我们的模型参数很多，模型复杂度高，容易发生过拟合。比如我们常说的 “small n, large p problem”。（我们一般用 n 表示数据点的个数，用 p 表示变量的个数，即数据维度。当 $p\gg n$ 的时候，不做任何其他假设或者限制的话，学习问题基本上是没法进行的。因为如果用上所有变量的话， p 越大，通常会导致模型越复杂，但是反过来 n 又很小，于是就会出现很严重的 overfitting 问题。

这个时候，我们可以对参数 w 引入先验分布，降低模型复杂度。

二. Ridge Regression

我们对参数 w 引入协方差为 $\alpha$ 的零均值高斯先验。

$\begin{align*} L(w) & = p(\vec{y}|X;w)p(w)\\ & = \prod_{i=1}^{m} p(y^{(i)}|x^{(i)};\theta)p(w)\\ & = \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right)\prod_{j=1}^{n}\frac{1}{\sqrt{2\pi\alpha}}exp\left( -\frac{(w^{(j)})^2}{2\alpha} \right)\\ & = \prod_{i=1}^{m} \frac{1}{\sqrt{2\pi}\delta}exp\left( -\frac{(y^{(i)} - w^Tx^{(i)})^2}{2\delta^2} \right)\frac{1}{\sqrt{2\pi\alpha}}exp\left( -\frac{w^Tw}{2\alpha} \right) \end{align*}$

取对数：

$\begin{align*} l(w) & = \log L(w)\\ & = m \log \frac{1}{\sqrt{2\pi}\delta}+ n \log \frac{1}{\sqrt{2\pi\alpha}} - \frac{1}{\delta^2}\cdot \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2 - \frac{1}{\alpha}\cdot \frac{1}{2} w^Tw\\ \Rightarrow & w_{MAP_{Guassian}} = \arg \underset{w}{\min} \left( \frac{1}{\delta^2}\cdot \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2 + \frac{1}{\alpha}\cdot \frac{1}{2} w^Tw \right) \end{align*}$

等价于：

$J_R(w) = \frac{1}{n}\lVert y- w^TX \rVert_2 + \lambda \lVert w \rVert_2$

这不就是 Ridge Regression 吗？

看我们得到的参数，在零附近是不是很密集，老实说 ridge regression 并不具有产生稀疏解的能力，也就是说参数并不会真出现很多零。假设我们的预测结果与两个特征相关，L2正则倾向于综合两者的影响，给影响大的特征赋予高的权重；而L1正则倾向于选择影响较大的参数，而舍弃掉影响较小的那个。实际应用中 L2正则表现往往会优于 L1正则，但 L1正则会大大降低我们的计算量。

Typically ridge or ℓ2 penalties are **much better** for minimizing prediction error rather than ℓ1 penalties. The reason for this is that when two predictors are highly correlated, ℓ1 regularizer will simply pick one of the two predictors. In contrast, the ℓ2 regularizer will keep both of them and jointly shrink the corresponding coefficients a little bit. Thus, while the ℓ1 penalty can certainly reduce overfitting, you may also experience a loss in predictive power.

那现在我们知道了，对参数引入高斯先验等价于L2正则化。

三. LASSO

上面我们对 w 引入了高斯分布，那么拉普拉斯分布(Laplace distribution)呢？

注：LASSO - least absolute shrinkage and selection operator.

我们看下拉普拉斯分布长啥样：

$f(x\mid\mu,b) = \frac{1}{2b} \exp \left( -\frac{|x-\mu|}{b} \right)$

关于拉普拉斯和正态分布的渊源，大家可以参见正态分布的前世今生。

重复之前的推导过程我们很容易得到：

$w_{MAP_{Laplace}} = \arg \underset{w}{\min} \left( \frac{1}{\delta^2}\cdot \frac{1}{2} \sum_{i=1}^{m} (y^{(i)} - w^Tx^{(i)})^2 + \frac{1}{b^2}\cdot \frac{1}{2} \lVert w \rVert_1 \right)$

该问题通常被称为 LASSO (least absolute shrinkage and selection operator) 。LASSO 仍然是一个 convex optimization 问题，不具有解析解。它的优良性质是能产生稀疏性，导致 w 中许多项变成零。再次总结下，对参数引入拉普拉斯先验等价于 L1正则化。

四. Elastic Net

可能有同学会想，既然 L1和 L2正则各自都有自己的优势，那我们能不能将他们 combine 起来？可以，事实上，大牛早就这么玩过了。因为lasso在解决之前提到的“small n, large p problem”存在一定缺陷。

这个我们就直接给结果了，不推导了哈。（好麻烦的样子。。。逃）

$\hat{\beta} = \arg \underset{\beta}{\min} \lVert y - X\beta \rVert_2 + \lambda_2 \lVert \beta \rVert_2 + \lambda_1 \lVert \beta \rVert_1$

五. 总结

正则化参数等价于对参数引入先验分布，使得模型复杂度变小（缩小解空间），对于噪声以及 outliers 的鲁棒性增强（泛化能力）。整个最优化问题从贝叶斯观点来看是一种贝叶斯最大后验估计，其中正则化项对应后验估计中的先验信息，损失函数对应后验估计中的似然函数，两者的乘积即对应贝叶斯最大后验估计的形式。

欢迎访问我博客：Regularized Regression: A Bayesian point of view

[1]: Bias 和 Variance

[2]: 《A Few useful things to Know About machine Learning》读后感

[3]: What is the difference between L1 and L2 regularization?

[4]: Bayesian Linear Regression

[5]: Bayesian statistics and regularization

[6]: 最大似然估计和最小二乘法怎么理解？ - 计算机

[7]: Sparsity and Some Basics of L1 Regularization

codestorm04

关注

1
点赞
踩
11

收藏

觉得还不错? 一键收藏
0
评论
L1、L2正则化与贝叶斯先验分布的关系

转自：https://note.youdao.com/ynoteshare1/index.html?id=2851b97199bcdc174001d72b1bec0372&type=note（1）频率学观点：认为参数w是固定的，数据集D有多个，所以要解决的问题是什么样的w能使当前的D出现的可能性最大假设给定输入x，其对应的label是t，且t服从高斯分布且均值为f(x)=wx+b...
复制链接

扫一扫