STM32CubeIDE嵌入式开发入门到入坟-软件篇-3、GPIO（IO）输入与良好的工程结构

原创已于 2025-10-13 21:33:03 修改 · 577 阅读

12 ·

CC 4.0 BY-SA版权

文章标签：

#stm32 #嵌入式硬件 #单片机 #STM32CubeIDe #嵌入式开发 #嵌入式工具 #软件工程结构

于 2025-10-13 21:09:52 首次发布

STM32CubeIDE开发专栏收录该内容

55 篇文章

订阅专栏

STM32CubeIDE嵌入式开发入门到入坟-软件篇-2、新建工程与GPIO（IO）口配置

续上一篇讲了IO的输出，这节我们来学习IO的输入以及建立一个良好的工程代码结构。

【STM32CubeIDE整理代码与目录结构以及问题】

一、GPIO（IO）口输入。

接着上一篇的工程，打开上一篇工程配置界面准备配置IO。先看硬件，我这里有个按键对应的IO是PC13，默认状态是外部下拉电阻将电平拉低，按键按下电平被拉高。

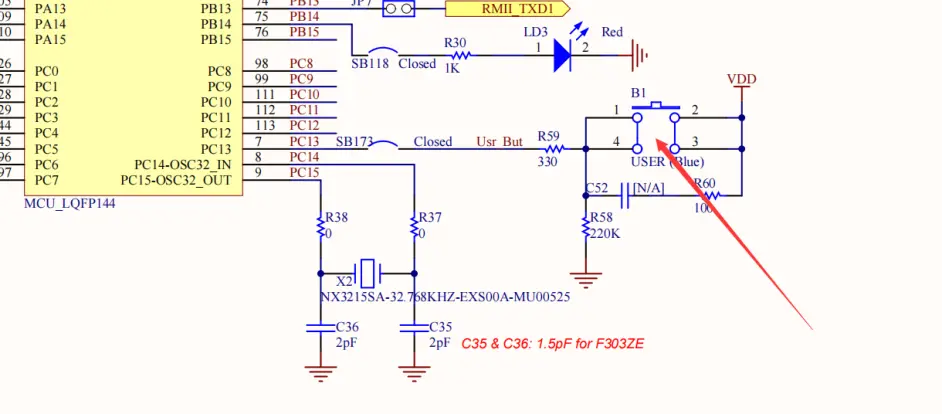
早到你所使用的按键对应的IO，在配置界面找到并配置为输入模式。

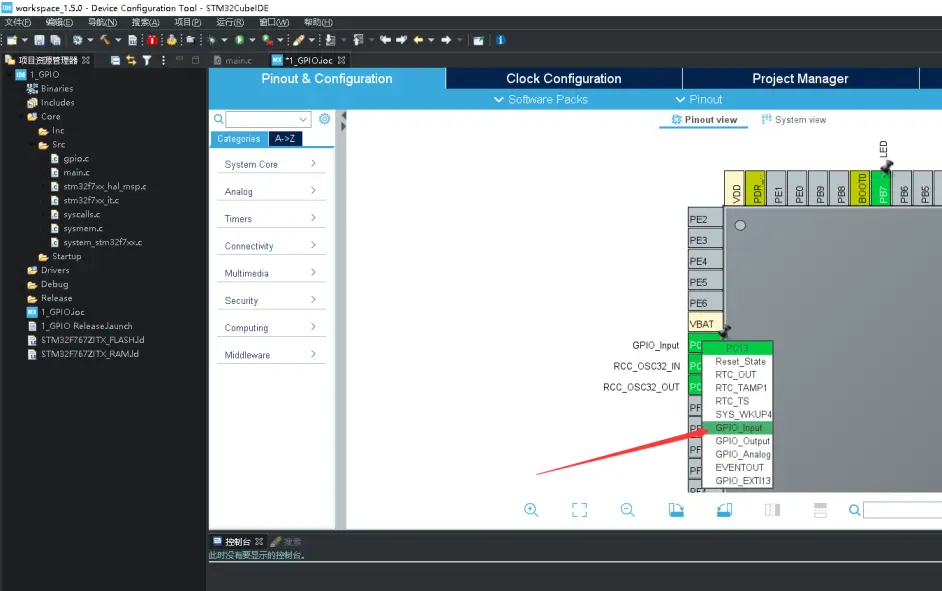
输入自定义名称（用默认名称也是可以的）。

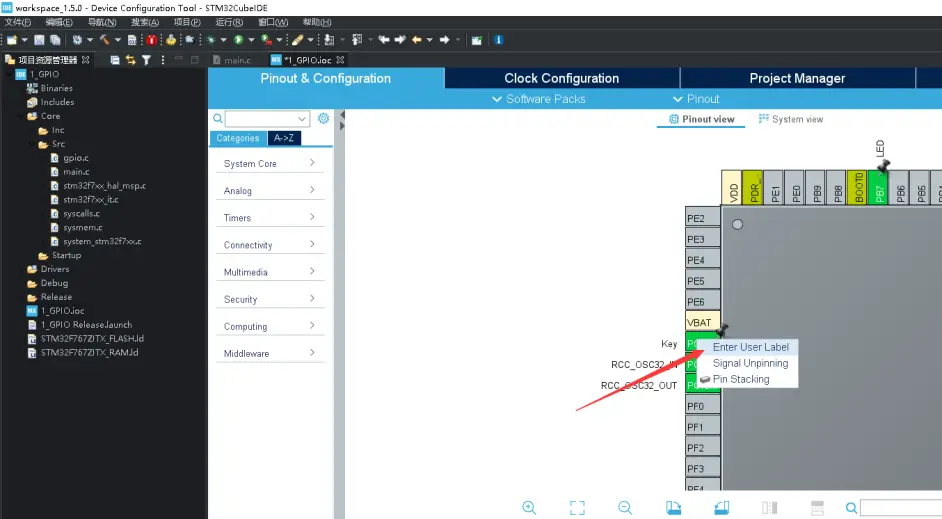
这里我们配置IO既不上拉也不下拉，因为外部硬件已经下拉了，STM32内部上下拉电阻典型值40KΩ，我们计算一下这里配置为下拉也可已，但是注意一般硬件的上下拉电阻不能太小，1K以上合适，太小可能会导致另一个电平拉高或拉低不了。

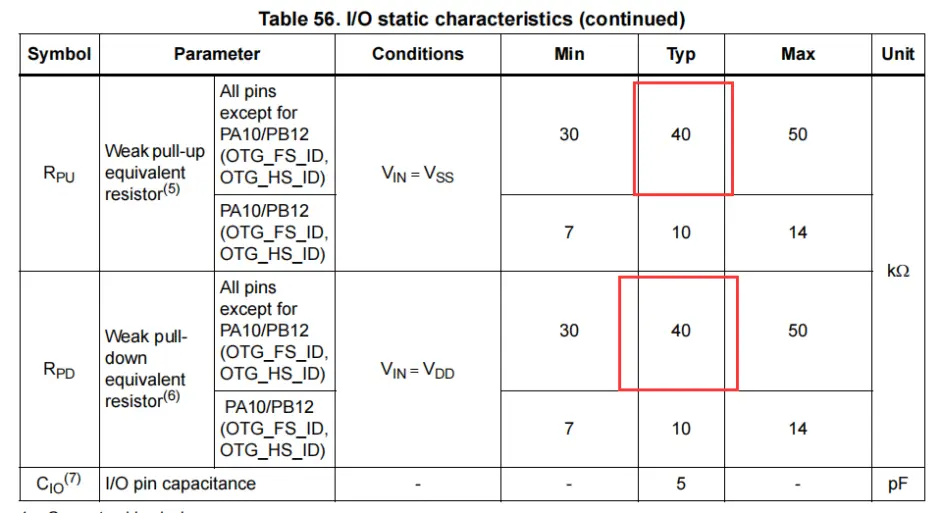
IO输入电平>0.7VDD电平为高，小于0.3VDD为低。中间电平状态就不可预测了。

好了，我们点击重新构建代码。

我们所有的自定义名称宏定义都在main.h中。

构建完成会发现我们上次写的代码消失了，这就是因为没有写在BEGIN与END之间的后果。如果发现自己很不巧没有写在里面，可以Ctrl+Z恢复。

读取引脚电平的函数：

HAL_GPIO_ReadPin(GPIOx, GPIO_Pin);

我们Ctrl+鼠标左键可以跳转带声明与实现，一路跟踪可以发现这个函数返回值是一个枚举定义的值。

/**
* @brief GPIO Bit SET and Bit RESET enumeration
*/
typedef enum
{
    GPIO_PIN_RESET = 0,
    GPIO_PIN_SET
}GPIO_PinState;

返回值有：GPIO_PIN_RESET = 0与GPIO_PIN_SET=1两个。我们写个if语句来判断我们的按键状态，并控制我们上一篇的LED灯。0对应False（假）,非零即正负数为True（真）。在while循环中写入代码：

if(HAL_GPIO_ReadPin(Key_GPIO_Port, Key_Pin)){                    //按下按键
    HAL_GPIO_WritePin(LED_GPIO_Port, LED_Pin, GPIO_PIN_SET);     //亮
}else{
    HAL_GPIO_WritePin(LED_GPIO_Port, LED_Pin, GPIO_PIN_RESET);    //灭
}

下载程序。当我们按下按键灯亮，放开按键灯灭。下

那怎么实现按一下LED翻转一下状态呢？

反转IO口电平的函数：

HAL_GPIO_TogglePin(GPIOx, GPIO_Pin);

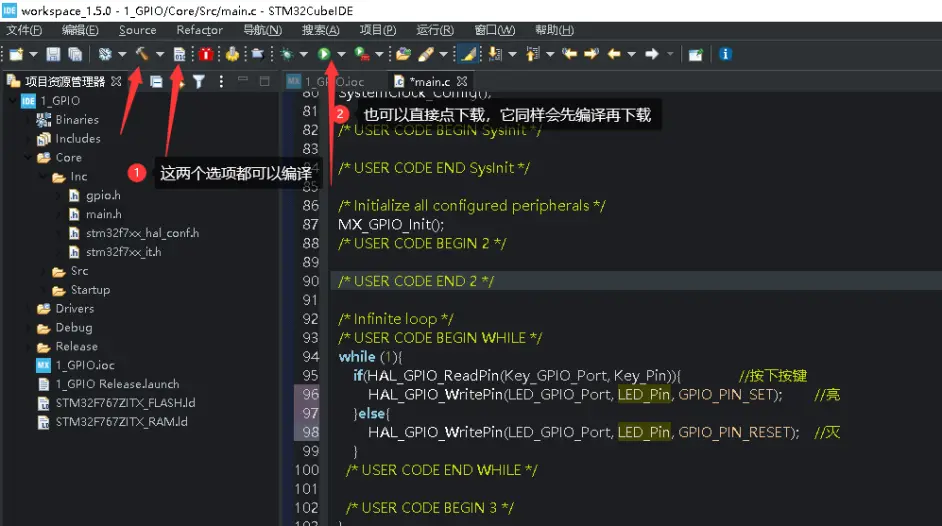
用if判断按键，在while循环中写入代码：

if(HAL_GPIO_ReadPin(Key_GPIO_Port, Key_Pin)){        //按下按键
	HAL_Delay(50);                                    //延时防止按下按键的抖动误判
	HAL_GPIO_TogglePin(LED_GPIO_Port, LED_Pin);        //翻转LED
	while(HAL_GPIO_ReadPin(Key_GPIO_Port, Key_Pin));    //等待按键松开
}

按键抖动厉害，led翻转不稳定可以加长延时时间改善。

编译下载即可控制了，不用while等待也可以使用变量作为一个标志来判断控制等，同学们多开动脑筋多尝试额。

二、良好的工程结构

在实际编写代码的过程当不可能将所有代码都写在main.c文件里，当然实际你将无数代码写在一行都行。但是咋看啊，自己也不方便管理。所以有个良好的结构是必须的。

我们先在Core文件夹下建立一个跟我们工程相关的名称，这里我新建MyGPIO。

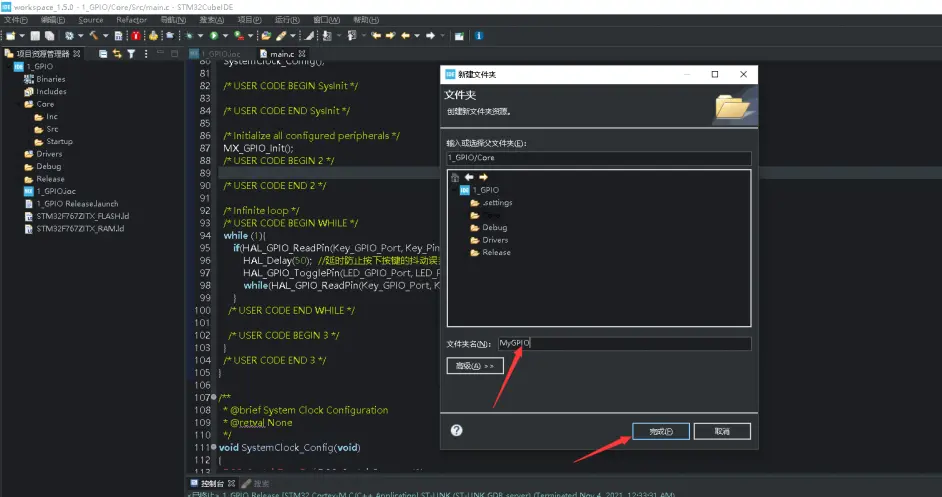
这里我们将这个文件夹作为我们自己编写代码的总文件夹，再在里面进行分类创建文件夹和代码。我们给我们的按键和LED灯创建一个文件夹。然后再新建相关功能文件，将代码模块化。

创建led.h led.c key.h key.c文件

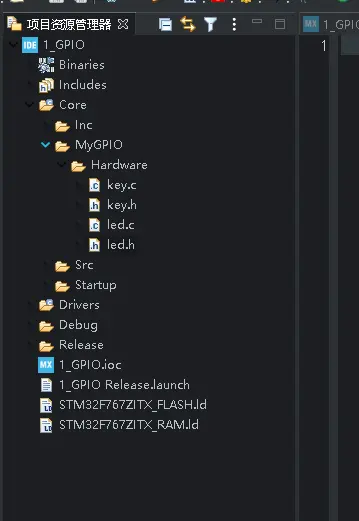
这里例子将功能自己使用函数封装起来，方便使用管理。

led.h 文件:

#include "stm32f7xx.h"

//宏定义：就是编译的时候会将所有包含这个头文件的ON替换为1编译（OFF同）
#define    ON    1
#define    OFF    0

void led(uint8_t state);    //声明LED控制函数

led.c 文件:

#include "led.h"
#include "main.h"

void led(uint8_t state){    //控制LED（参数传入ON或者OFF）
    if(state){
        HAL_GPIO_WritePin(LED_GPIO_Port, LED_Pin, GPIO_PIN_SET);        //亮
    }else{
        HAL_GPIO_WritePin(LED_GPIO_Port, LED_Pin, GPIO_PIN_SET);        //灭
    }
}

key.h 文件:

#include "stm32f7xx.h"

uint8_t readKeyState();        //声明读取按键电平自己的封装函数

key.c 文件:

#include "key.h"
#include "main.h"

uint8_t readKeyState(){
    return        HAL_GPIO_ReadPin(Key_GPIO_Port, Key_Pin);        //返回读取到的电平
}

在main.c包含我们写的两个头文件

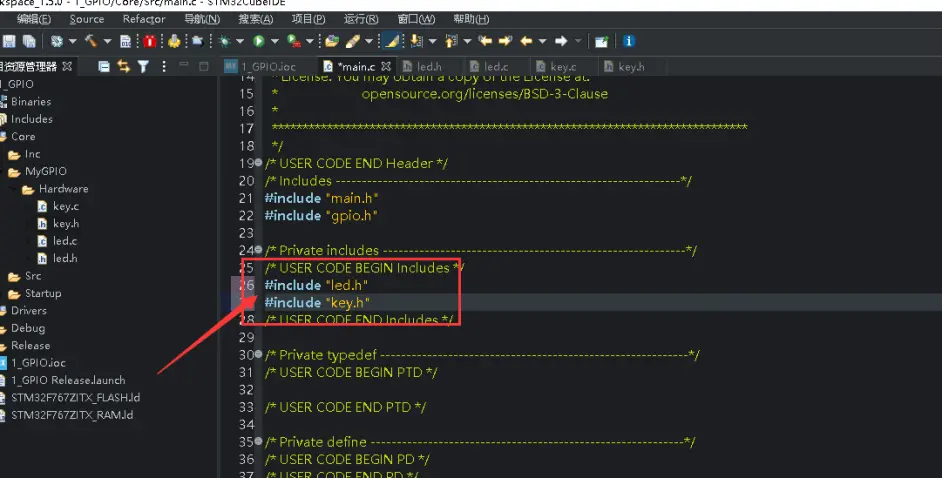
再让工程包含扫描我们自己编写代码的文件夹：

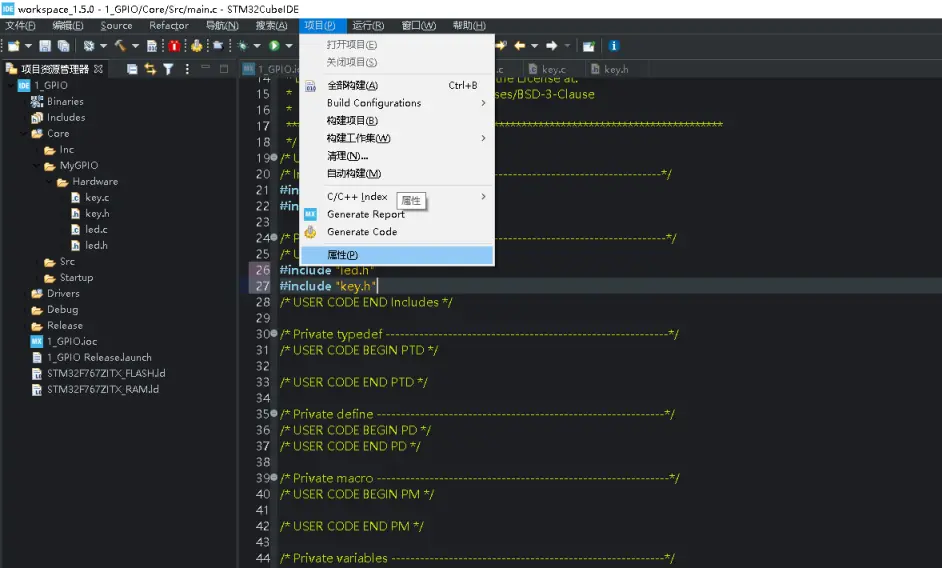
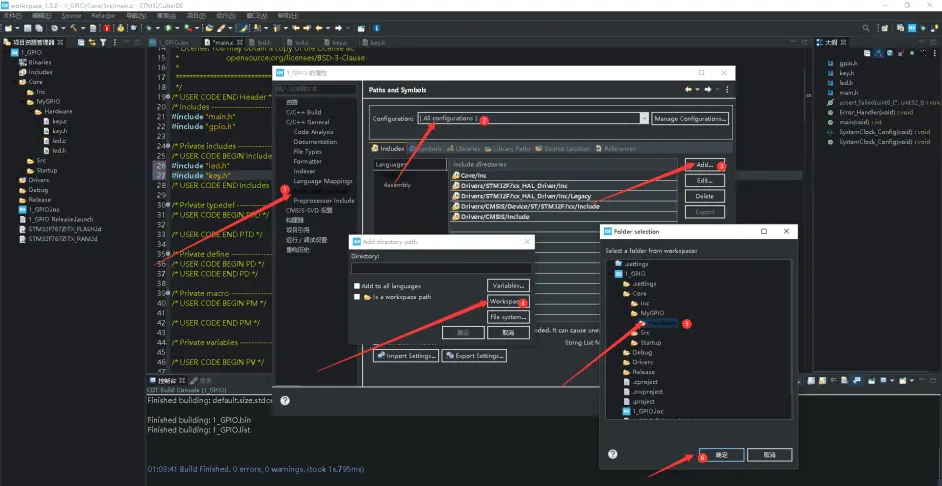
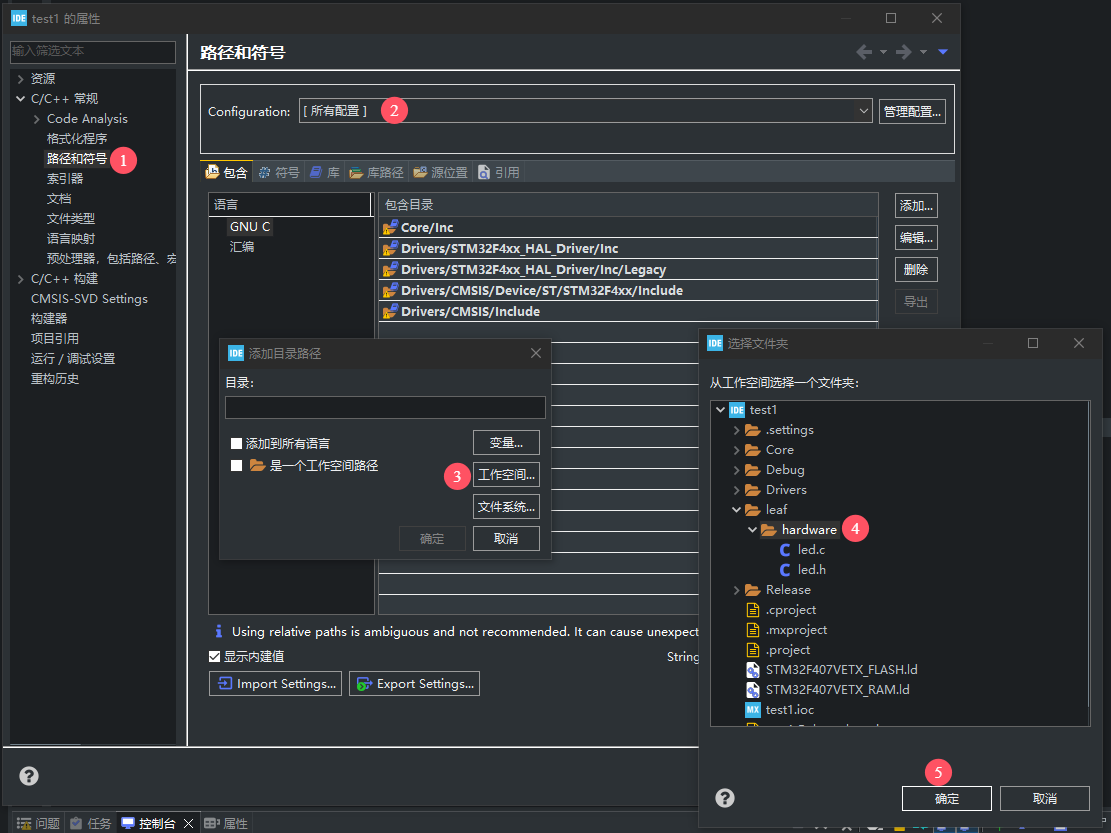
或者创建文件夹的时候使用下图方式：

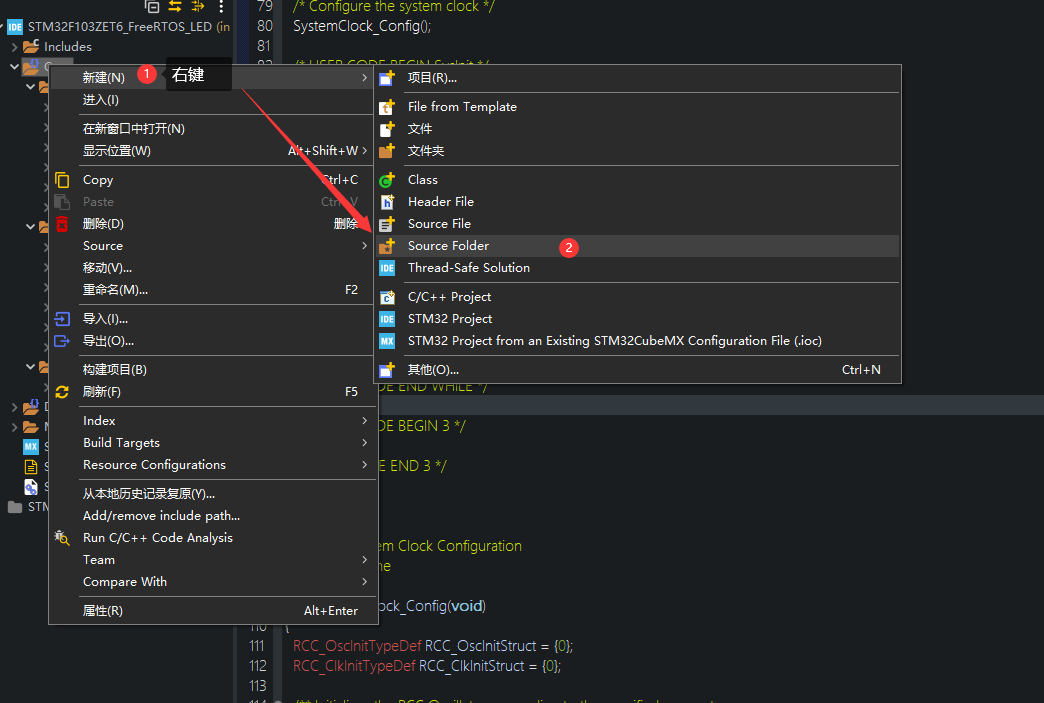
已经创建好的文件夹可以使用下图方式添加路径：

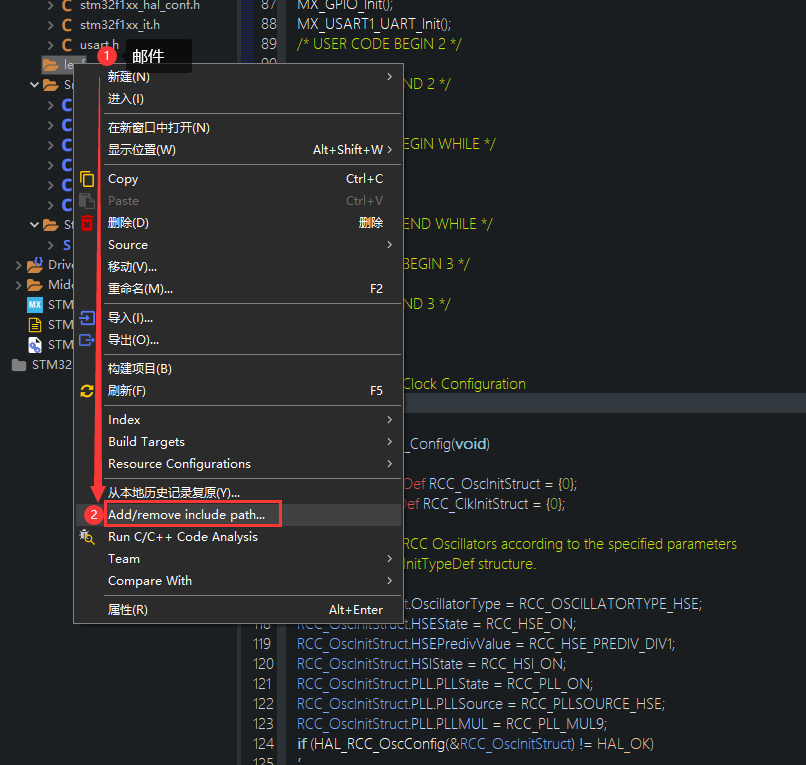
好了确认应用，编译没有错误。我们就可以在mian.c使用我们刚刚封装好的函数了。

led(ON);    //LED亮
led(OFF);    //LED灭
readKeyState();    //得到Key按键电平

好了我们IO口的学习就到此结束。后面将学习STM32外设了。