欧拉函数
-
定义:对于正整数n,欧拉函数是小于n的正整数中与n互质的数的数目
-
通式:
【其中:p1,p2,...,pn为x的所有质因数,x是不为0的整数】
-
特别说明:φ(1)=1:和1互质的数(<=1)就是1本身
-
性质:
- 若n为质数,φ(n)=n-1
- 若m,n互质,φ(mn)=φ(m)φ(n)
- 当n为奇质数时,φ(2n)=φ(n)
- 当n=p^k,且p是质数时,
证明:[1,n-1]即[1,p^k-1]区间有整数p^k-1个
与p^k不互质的数有{p,2p,3p,4p,...,p^k-p(=(p^(k-1)-1)*p}明显有p^(k-1)-1个
于是前者-后者得到:
也就是:![]()
//欧拉函数模板
bool Is_Prime(ll x)
{
if( x == 2 ) return true;
for(ll i = 2 ; i * i <= x ; i++)
{
if( x % i == 0)
return false;
}
return true;
}
set<ll> st;
void prime_factor(ll x)
{
for(ll i = 2 ; i <= x ; i++)
{
if(Is_Prime(x))
{
st.insert(x) ;
return ;
}
if(Is_Prime(i))
{
while(x % i == 0)
{
x /= i;
st.insert(i);
}
}
}
}
ll Euler(ll x)
{
if(x == 1) return 1;
ll up = x, down = 1;
prime_factor(x);
while(! st.empty())
{
int tmp = *st.begin();
st.erase(st.begin());
up *= (tmp - 1);
down *= tmp;
}
return up / down;
}
欧拉定理
同余定理:
- 两个整数a,b,若它们除以整数m所得的余数相等,则称a与b对模m同余或a同余于b模m,记作:a≡b(mod m)
- 给定一个整数m,如果两个整数a,b满足(a-b)%b=0,那么a与b对模m同余,记作a-b≡0(mod m),也即m|(a-b)
内容:
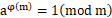 其中a和m互质
其中a和m互质
证明:
假设小于m且与m互质的数为{x[1],x[2],x[3],...,x[φ(m)]},令p[ i ]=a*x[ i ],得到{p[1]=a*x[1], p[2]=a*x[2], ... ,p[φ(m)]=a*x[φ(m)]}
引理1:
- p[ ]之间两两对于模m不同余;x[ ]之间两两对于模m不同余
证明:
假设p[ i ]和p[ j ]对于模m同余(p[ i ]>p[ j ],i != j),即p[ i ]-p[ j ] Ξ 0 (mod m)
那么m|p[ i ]-p[ j ] -> m|a(x[ i ]-x[ j ])
设a(x[ i ]-x[ j ])=km (k是整数)
因为a和m互质,所以由上式的恒等性可以得到:x[ i ]-x[ j ]和m不互质,且x[ i ]-x[ j ]是m的倍数,即x[ i ]-x[ j ] Ξ 0 (mod m),也就是x[ i ]与x[ j ]对模m同余
又因为x[ i ]和x[ j ]都与m互质,且都小于m,所以与上述结论矛盾
得证。
引理2:
- 每个p[ ]模m的结果都与m互质
证明:
假设p[ i ]=ax[ i ]=km+r, gcd(r,m)>1【也就是r和m有公因子,我们设为d,也即d|r,d|m】
原式可以化为:ax[ i ]=d*(km/d+r/d),即 d|ax[ i ]
因为a和m互质,x[ i ]和m互质,所以ax[ i ]和m互质,与上述结论矛盾
得证
由上面两个引理我们可以得到:
p[ ]%m的集合和x[ ]的集合相等,即p[ ]重新排序后与x[ ]对应,两两对模m同余。
我们将p[ ]相乘 :![]() =
= ![]() *
* ![]()
因为p[ i ] Ξ x[ i ] (mod m)
所以![]() Ξ
Ξ ![]() (mod m) 【由引理1和欧拉函数的性质2】
(mod m) 【由引理1和欧拉函数的性质2】
也即![]() *
* ![]() Ξ
Ξ ![]() (mod m)
(mod m)
即![]() Ξ 1 (mod m)
Ξ 1 (mod m)
至此,欧拉定理得证
费马小定理
- p为质数,整数a不是p的倍数,则a^(p-1)Ξ1(mod p)
扩展欧拉定理








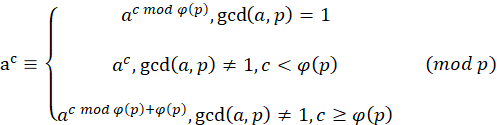














 918
918











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








