回溯算法 + 剪枝专题

       回溯算法，相比大家再熟悉不过了，全排列、八皇后、迷宫问题、人狼羊菜过河、人鬼渡河等问题都可用回溯算法解决，但我们如何解决这类问题呢?
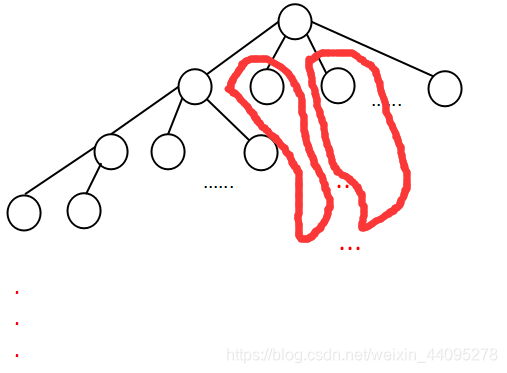
       回溯实质上也是枚举，即可尝试所有情况，我们来看一张图:

       画的不是很标准，但勉强能看，这是一棵满 n 叉树，可以借用此模型来理解回溯算法，即层层深入，直到叶子节点(底层)才返回，返回上一父节点，继续进入下一节点，直至遍历完整棵满 n 叉树。
       代码架构如下:

#include <iostream>
#include <algorithm>
using namespace std;

int n, x[1024], cnt = 0;//x[]存放排列内容 

void OutPut()
{
   
   
	printf("%d :", ++cnt);
	for(int i = 1; i <= n; ++i) printf("%d ", x[i]);
	putchar('\n');
}

void Full_Permutation(int k)
{
   
   
	if(k > n) OutPut();
	else
	{
   
   
		for(int i = 1; i <= n; ++i)
		{
   
   
			x[k] = i; 
			Full_Permutation(k + 1);	
		} 
	}
}

int main()
{
   
   
	scanf("%d", &n);
	Full_Permutation(1);
	return 0;
}

       这是最简单也是最初的回溯模型，即无任何条件限制(没有剪枝)，但如果我们要输出全排列，即每个数字均不相同，这时需要进行剪枝，即在for循环下卡住对应的条件即每位数字不相等，与前面的数字一一比较即可。
       全排列(未优化)

void OutPut()
{
   
   
	printf("%d :", ++cnt);
	for(int i = 1; i <= n; ++i) printf("%d ", x[i]);
	putchar('\n');
}

//////////////////////////////////////
if(Prune(k, i))//剪枝 
{
   
   
	x[k] = i; 
	Full_Permutation(k + 1);	
} 

       关键点来了，这我需要每次都与前面记录的数相比较，付出了$O(n)$级别的代价，那我能否在一开始采用一个一维数组记录它是否被纳入x[]数组中呢?
       答案当然可以

      &nb