计算最大公约数最小公倍数（C++实现）

华为的一道机考题，记录一下思路

手下是数学方法解析，算最小公倍数，需要用到最大公约数。首先将用计算机算法算最大公约数的原理。

最大公约数

辗转相除法(欧几里得 Euclidean）
　　
　　用“较大数”除以“较小数”，再用较小数除以第一余数，再用第一余数除以第二余数；反复直到余数为零为止。
　　图解：
　　

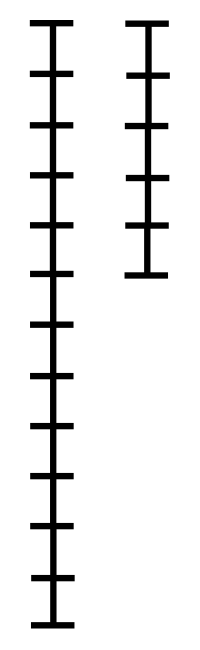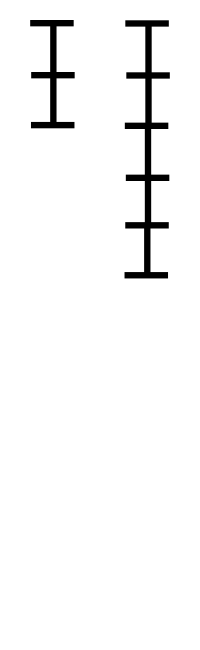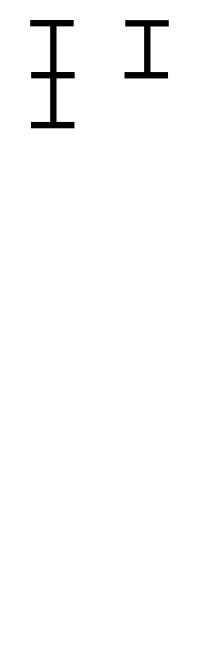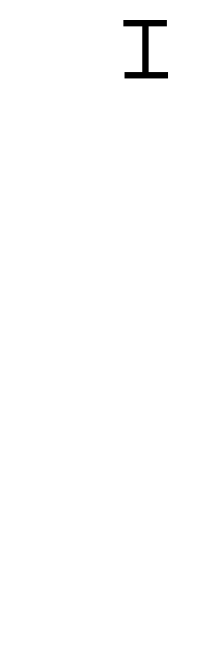
代码实现：

//迭代
int gcd(int a, int b) // greatest common divisor 最大公约数
{
    while(a%b){
        int tmp = a;
        a = b;
        b = tmp%b;
    }
    return b;
 
}
//递归
int gcd(int a,int b)
{
    if(b == 0)
        return a;
    return gcd(b,a%b);
}

最小公倍数

首先考虑人工算法。分解质因数法。
比如求45和30的最小公倍数。

45=3*3*5
30=2*3*5

不同的质因数是2。5，3是他们两者都有的质因数，由于45有两个3，30只有一个3，所以计算最小公倍数的时候乘两个3.
　　最小公倍数等于2 * 3 * 3 * 5=90
　　又如计算36和270的最小公倍数
　　36=2 * 2 * 3 * 3
　　270=2 * 3 * 3 * 3 * 5
　　不同的质因数是5。2这个质因数在36中比较多，为两个，所以乘两次；3这个质因数在270个比较多，为三个，所以乘三次。
　　最小公倍数等于2 * 2 * 3 * 3 * 3 * 5=540

而通过知道最大公约数，比如45和30的最大公约数为15，即相同的质因数之积为15，两数之积除以最大公约数即去掉相同的质因数，结果为2 * 3 * 3 * 5=90

所以：
最小公倍数 = 两数之积除以最大公约数

代码实现：

#include<iostream>
using namespace std;
 
int gcd(int a, int b) // greatest common divisor 最大公约数
{
    while(a%b){
        int tmp = a;
        a = b;
        b = tmp%b;
    }
    return b;
 
}
int main()
{
    int a,b;
    while(cin >> a >> b){
        cout << a*b/gcd(a,b) <<endl;
    }
    return 0;
}

参考文献：
https://baike.baidu.com/item/%E6%9C%80%E5%A4%A7%E5%85%AC%E7%BA%A6%E6%95%B0/869308?fr=aladdin

https://www.cnblogs.com/lvmf/p/10758468.html

https://baike.baidu.com/item/%E6%9C%80%E5%B0%8F%E5%85%AC%E5%80%8D%E6%95%B0/6192375?fr=aladdin