海杂波统计特性分析

实验的背景和意义

海杂波特性认知研究是一项极其复杂的系统工程。海杂波是影响海用雷达目标探测性能的主要制约因素之一，其物理机理复杂，影响因素众多，且非高斯、非平稳特性显著。

数据简介：

1. 雷达照射海面形成的回波称为海杂波
2. 在短时间内，海杂波可以用平稳随机过程来描述

​​​​​​​

 

 

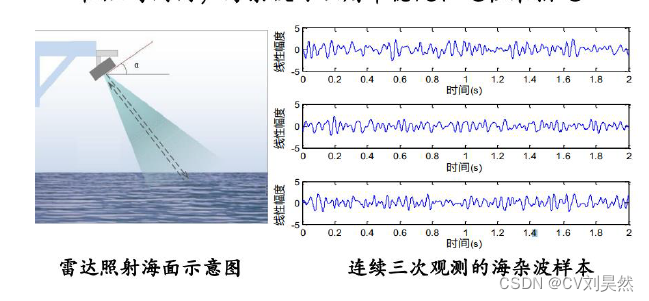
1. 每组数据有约130000个复数据点，仅分析数据的实部
2. 经过方差归一化处理

 

…………………………………………………………………………………………………………………

二、实验目标和内容

随机过程的数字特征：

对具有各态历经性的平稳随机过程（采样后的信号)：

1. 均值

 

1. 方差

 

1. 自相关函数

 

1. 功率谱密度GX(w)

 

对具有各态历经性的平稳随机过程，将一条较长的样本x(t)截成若干小段，等效地获得多条样本函数，从而使得估计结果更加平滑。

 

…………………………………………………………………………………………………………………

• 实验方案和技术路线

利用Matlab实现对具有各态历经性的平稳随机过程的数据分析：

以海杂波数据为例估计随机过程的数字特征

1. 均值、方差、概率密度函数
2. 自相关函数
3. 功率谱密度

估计方法对具有各态历经性的平稳随机过程有效基于数字特征比较不同海况下海杂波的特点进行分析：

高海况：

clear hi_data_file = fopen('hi.dat','r'); hi_data=fscanf(hi_data_file,'%g'); %复数的实部+虚部序列 data_len = length(hi_data) / 2; re_hi_data = zeros(data_len, 1);%实部  in-phase im_hi_data = zeros(data_len, 1);%虚部  quadrature %将数据转成数组 data_index = 1; for i = 1 : 2 : data_len * 2     re_hi_data(data_index) = hi_data(i);     im_hi_data(data_index) = hi_data(i+1);     data_index = data_index + 1; end complex_hi_data = complex(re_hi_data, im_hi_data);%复数 time_span = 0.001; t = 0 : time_span : time_span * (data_len- 1);%时间轴 %计算实部特性 hi_data_mean = mean(re_hi_data);%均值 hi_data_var = var(re_hi_data);%方差 histogram(re_hi_data);%直方图(PDF) figure;%创建一个图像窗口 ksdensity(re_hi_data);%拟合概率密度函数 figure;%创建一个图像窗口 normplot(re_hi_data);%正态概率低，检验不符合高斯分布 [h, p] = chi2gof(re_hi_data);%拟合度曲线，检验出不符合高斯分布(因为p=0) figure;%创建一个图像窗口 %计算自相关,间隔两秒 r_span = 2 / 0.001; r_hi_data_sum = zeros(2 * r_span-1, 1); for i = 1 : r_span : floor(data_len / r_span) * 2000     r_hi_data = xcorr(re_hi_data(i : i+r_span - 1));     r_hi_data_sum = r_hi_data_sum + r_hi_data; end r_hi_data_num = length(1 : r_span : floor(data_len / r_span)); r_hi_data_sum = r_hi_data_sum ./ r_hi_data_num;%求平均 r_t = -time_span * (r_span- 1) : time_span : time_span * (r_span - 1);%时间轴 plot(r_t, r_hi_data_sum) figure;%创建一个图像窗口 %计算功率谱，间隔两秒 (PSD) p_span = 2 / 0.001; p_window = boxcar(p_span); nfft = 1024; p_hi_data_sum = zeros(nfft / 2 + 1, 1); f_axis = zeros(nfft / 2 + 1, 1); for i = 1 : p_span : floor(data_len / p_span) * 2000     [p_hi_data, f_axis] = periodogram(re_hi_data(i : i+r_span-1), p_window, nfft, 1 / 0.001);     p_hi_data_sum = p_hi_data_sum + p_hi_data; end p_hi_data_num = length(1 : r_span : floor(data_len / r_span)); p_hi_data_sum = p_hi_data_sum ./ p_hi_data_num;%求平均 %plot(f_axis, 10*log10(p_hi_data_sum)) plot(f_axis, p_hi_data_sum)

低海况：

clear hi_data_file = fopen('lo.dat','r'); hi_data=fscanf(hi_data_file,'%g'); %复数的实部+虚部序列 data_len = length(hi_data) / 2; re_hi_data = zeros(data_len, 1);%实部  in-phase im_hi_data = zeros(data_len, 1);%虚部  quadrature %将数据转成数组 data_index = 1; for i = 1 : 2 : data_len * 2     re_hi_data(data_index) = hi_data(i);     im_hi_data(data_index) = hi_data(i+1);     data_index = data_index + 1; end complex_hi_data = complex(re_hi_data, im_hi_data);%复数 time_span = 0.001; t = 0 : time_span : time_span * (data_len- 1);%时间轴 %计算实部特性 hi_data_mean = mean(re_hi_data);%均值 hi_data_var = var(re_hi_data);%方差 histogram(re_hi_data);%直方图(PDF) figure;%创建一个图像窗口 ksdensity(re_hi_data);%拟合概率密度函数 figure;%创建一个图像窗口 normplot(re_hi_data);%正态概率低，检验不符合高斯分布 [h, p] = chi2gof(re_hi_data);%拟合度曲线，检验出不符合高斯分布(因为p=0) figure;%创建一个图像窗口 %计算自相关,间隔两秒 r_span = 2 / 0.001; r_hi_data_sum = zeros(2 * r_span-1, 1); for i = 1 : r_span : floor(data_len / r_span) * 2000     r_hi_data = xcorr(re_hi_data(i : i+r_span - 1));     r_hi_data_sum = r_hi_data_sum + r_hi_data; end r_hi_data_num = length(1 : r_span : floor(data_len / r_span)); r_hi_data_sum = r_hi_data_sum ./ r_hi_data_num;%求平均 r_t = -time_span * (r_span- 1) : time_span : time_span * (r_span - 1);%时间轴 plot(r_t, r_hi_data_sum) figure;%创建一个图像窗口 %计算功率谱，间隔两秒 (PSD) p_span = 2 / 0.001; p_window = boxcar(p_span); nfft = 1024; p_hi_data_sum = zeros(nfft / 2 + 1, 1); f_axis = zeros(nfft / 2 + 1, 1); for i = 1 : p_span : floor(data_len / p_span) * 2000     [p_hi_data, f_axis] = periodogram(re_hi_data(i : i+r_span-1), p_window, nfft, 1 / 0.001);     p_hi_data_sum = p_hi_data_sum + p_hi_data; end p_hi_data_num = length(1 : r_span : floor(data_len / r_span)); p_hi_data_sum = p_hi_data_sum ./ p_hi_data_num;%求平均 %plot(f_axis, 10*log10(p_hi_data_sum)) plot(f_axis, p_hi_data_sum)

• 实验结果和分析

海杂波特征估计实例：

1、使用海杂波数据计算随机过程的数字特征：均值、方差、概率密度函数、自相关函数、功率谱密度。

2、估计方法对具有各态历经性的平稳随机过程有效；

3、基于数字特征比较不同海况下海杂波特点。

 

当雷达照射海面形成的回波称为海杂波，在短时间内，海杂波可以用平稳随机过程来描述。

对高海况和低海况的海杂波的特性进行分析：均值、方差、高斯分布程度、自相关、自相关时间、功率谱进行分析。对比和区分两种海况的特性。

1、高斯分布程度分析：

使用正态概率纸和拟合优度方法进行分析；

先绘制直方图：

 

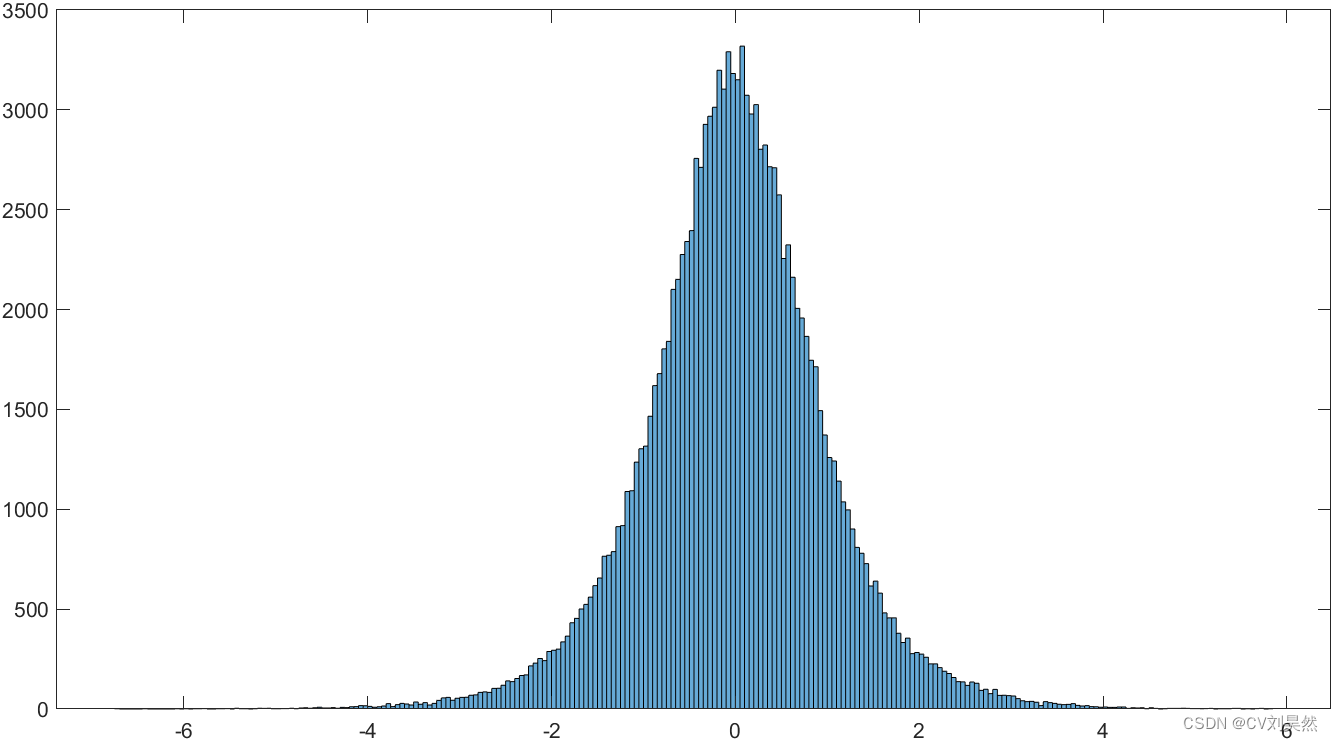
高海况直方图

 

低海况直方图

绘制概率密度图

 

高海况概率密度

 

低海况概率密度

绘制正态概率纸结果：

 

高海况正态概率图

 

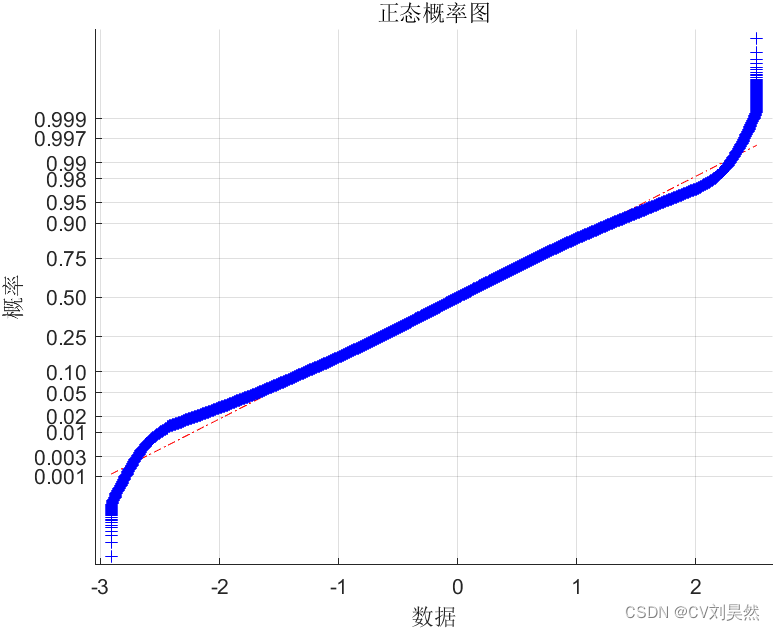
低海况概率密度图

 

最后计算拟合优度的概率值，正态概率低，检验不符合高斯分布

由拟合度曲线，可检验出不符合高斯分布(因为p=0)

2、自相关分析：

间隔两秒的时间窗截取信号，进行自相关分析，最后将每个时间窗的自相关结果进行求取平均值，得到海杂波的自相关特性曲线：

 

高海况自相关分析

 

低海况自相关分析

进一步计算自相关时间：

 

通过两种海况下ACF对比发现高海况下海杂波起伏更快，相关时间更小：

 

3、功率谱密度分析

间隔两秒的时间窗截取信号，进行功率谱密度分析，最后将每个时间窗的功率谱密度分析结果进行求取平均值，得到海杂波的功率谱密度分析特性曲线。

 

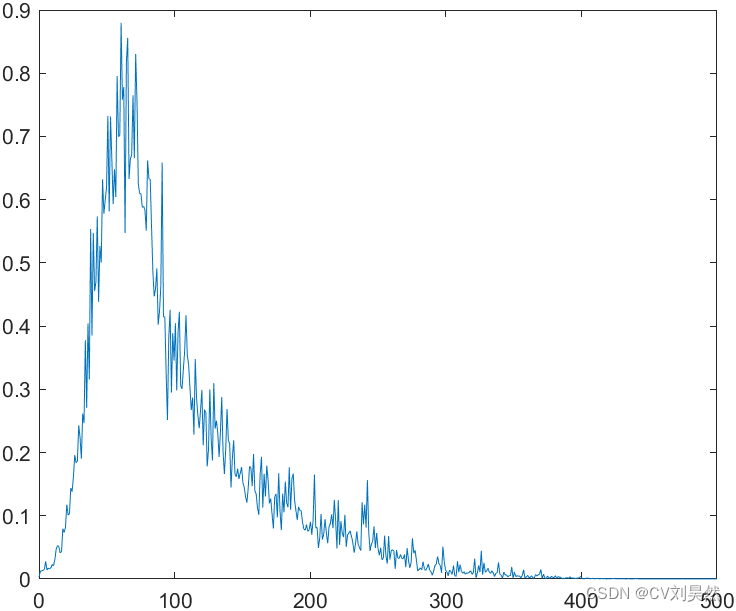
高海况功率谱密度

 

低海况功率谱密度

通过对两种海况下PSD对比发现高海况下海杂波平均速度更大：

 

…………………………………………………………………………………………………………………

五、实验结论：

1. 高海况表现出更具有的非高斯性；
2. 高海况自相关时间短于低海况；
3. 低海况功率谱密度窄一些；
4. 根据多普勒峰值频率计算的平均速度，高海况更大；

即高海况下海杂波更偏离高斯分布、起伏更快、多普勒速度更大

…………………………………………………………………………………………………………………

• 实验感悟

MATLAB中有丰富的图形处理能力，提供了绘制各种图形、图像数据的函数。他提供了一组绘制二维和三维曲线的函数，他们还可以对图形进行旋转、缩放等操作。MATLAB内部还包含丰富的数学函数和数据类型，使用方便且功能非常强大。通过对MATLAB的系统环境，数据的各种运算，矩阵的分析和处理，程序设计，绘图，数值计算及符号运算的学习，初步掌握了MATLAB的实用方法。