1.3 数学基础：函数与证明方法(Mathematical Foundations: functions and proof techniques)

1.3、数学基础：函数与证明方法 (functions and proof techniques)

1.3.1、函数(functions)

1.3.1.1、函数基本术语和例子 (Functions, basic terminology and examples)

(1)、函数 (Functions)

在许多应用中，我们给一个集合的每个元素赋值给另一个集合的特定元素。例如，我们可以模拟这个模块中的每个学生的分数如下所示。

例如:设S为本模块所有学生的集合，设grade:={Pass(及格)，merit(优秀)，distinction(优秀)，fail(不及格)}。然后用函数$f:S\to Grades$，其中$f(s):$= OCOM5102M Algorithms 中的等级s，对情况进行建模。

(2)、函数的定义 (Function: definition)

设A和B是非空集。函数f从A到B是B中的一个元素对A中的每个元素的赋值。

如果b是元素B的唯一元素，该元素由函数f赋值给A中的a元素。

如果 $f$ 是一个函数从 $A$ 到 $B$，我们写为 $f:A\to B$
注意：函数有时也叫做’映射’(mappings)或者’转换’(transformations)

(3)、函数的特殊关系 (Functions are special relations)

我们可以根据 A到B的关系来定义函数 $f:A\to B$。

为此，回忆一下从 A 到 B 的关系是 A $\times$B 的子集。

函数的其他定义：
从A 到B的关系包含确切的一个(a,b)对，对于每一个元素a$\in$A，这就叫做从 A 到 B 的函数 $f$。

这个函数是从 A 到 B，由赋值 $f(a)=b$给出，其中$(a,b)$是关系中以$a$为第一元素的唯一对(pair)。

(4)、域、上域、图像和原图像的定义 (Domain, codomain, image, preimage: definition)

假设 $f:A\to B$是一个函数，
集合$A$叫做函数$f$的定义域(domain)。
集合$B$叫做函数$f$的上域(codomain)。

如果 $f(a)=b$，
有$b$是$a$的像(image)。
有$a$是$b$的象原(preimage)。

$f$的值域(range, 也叫做象image)是A中所有象元素的集合。
同时，如果 $f$ 是一个从 $A$到$B$的函数，我们说$f$将$A$映射到$B$上。

(5)、指定函数 (Specifying functions)

当指定一个函数时，你总是需要说明：

1. 你选择哪个集合作为域(domain)
2. 你选择哪个集合作为上域(codomain)
3. 对于定义域中的每一个元素，你必须说明它被映射到上域的哪个元素

注意：
如果我们改变域或者上域，我们会有一个不同的函数。
如果我们改变元素的映射，我们也会有一个不同的函数。

1.3.1.2、单射、满射与双射 - Injective, surjective, bijective

(1)、单射的定义 (Injective: definition)

有些函数从不给两个不同不同的域元素赋相同的值。这些函数被称为’单射’(injective，或’一对一’，‘one-to-one’)

定义：一个函数 $f:A\to B$ 被叫做单射(或一对一)，当且仅当$f(a)=f(b)$意味着对于$f$的定义域A中的所有a和b，a=b。
自己的理解：定义域上任意两个不同元素的映射不会映射到同一值

注意：每当$a\ne b$，$a,b\in A$时，一个函数$f:A\to B$是单射的当且仅当 $f(a)\ne f(b)$

利用定义中蕴含的对位(contraposition)，得到$f$是单射的这种表示方法。

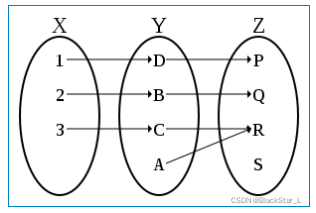
(2)、满射的定义 (Surjective: definition)

对于某些元素，值域和上域是相等的。也就是说，上域中的每个元素都是域中的某个元素的象，具有此属性的函数称为满射的(surjective,或’onto’)。

一个函数$f:A\to B$被称为满射，当且仅当对每个元素 $b\in B$存在一个元素$a\in A$且$f(a)=a$。
自己的理解：值域中的每个元素都有与之对应的定义域中的元素。

满射复合：第一个函数不必为满射

(3)、双射的定义 (Bijective: definition)

一个函数 $f$被称为双射(bilective,或一一对应 one-to-one correspondence)，如果它既是单射又是满射，我们就说这个函数是一个双射。

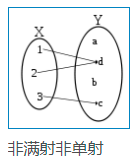
(4)、证明或伪证单射与满射的方法 (Recipies for proving/disproving injectivity and surjectivity)

假设 $f:A\to B$ 是一个函数：

• 证明 $f$ 是单射的，证明对于任意 $x,y\in A$当$f(x)=f(y)$时，那么有$x=y$。
• 证明 $f$ 不是单射的，寻找特殊元素 $x,y\in A$，满足 $x\ne y$ 并且 $f(x)=f(y)$。
• 证明 $f$ 是满射的，考虑一个任意元素$y\in B$，寻找一个元素$x\in A$满足$f(x)=y$。
• 证明 $f$ 不是满射的，寻找一个特殊元素$y\in B$，满足对所有$x\in A$，$f(x)\ne y$。

1.3.1.3、复合函数、逆函数、加法函数与乘法函数- Composition, inverse, addition and multiplication of functions

(1)、实值/整数值功能的定义(Real-valued/integer-valued function: definition)

如果函数的上域是实数的集合，则称为实值函数；如果函数的上域是整数的集合，则称为整值函数。

如果两个实值函数或者两个整值函数有相同的定义域，则可以相加或相乘。

(2)、函数相加或相乘的定义(Definition (adding/multiplying functions))

假设 $A$ 是一个集合，假设 $f$ 和 $g$ 是两个$A$到$R$(到$Z$)的函数。于是$f+g$ 和 $f\cdot g$ 是 $A$到$R$(到$Z$)的函数，对于所有 $x\in A$可以定义：

• $(f+g)(x):=f(x)+g(x)$
• $(f\cdot g)(x):=f(x)\cdot g(x)$

(3)、复合函数的定义(Composition of functions: definition)

#3## (4)、同一函数的定义(Identity function: definition)

(5)、逆函数的定义(Inverse function: definition)

举例：

(6)、定理

应用：

1.3.2、证明(Proof)

1.3.2.1、直接证明、对位证明和矛盾证明(Direct proof, proof by contraposition, proof by contradiction)

1.3.2.2、进一步的证明技术与常见错误(Further proof techniques and common mistakes)

1.3.2.3、归纳证明(Proof by induction)

参考：
单射、双射与满射