算法刷题总结 (三) 贪心算法

BlackStar_L

已于 2023-07-02 13:02:10 修改

阅读量1.4k

点赞数 14

分类专栏： Data Structures and Algorithms 文章标签：贪心算法数据结构区间问题序列问题股票问题

于 2023-03-15 20:34:24 首次发布

本文链接：https://blog.csdn.net/weixin_44225602/article/details/129567199

版权

算法总结3 贪心算法

一、理解贪心算法
二、经典题型
三、参考

一、理解贪心算法

在这里插入图片描述

1.1、贪心算法的概念

贪心算法是遵循在每个阶段做出局部最优选择从而解决启发式(近似最优解)问题的任何算法。

因为贪心策略在很多情况下不会产生最优解，可能大部分是近似最优解，也有小部分可能是最糟糕的结果。但对某些特殊问题，采用贪心可以取到最好的效果，即可以从局部最优可以推导到全局最优。

我们分别来看看两个例子：

例子1 (局部最优到全局最优)：

某货币有1, 5, 10 ,20的面值大小，现在要找给客户36面值大小的货币，要求找给的货币数量最少。

这里使用贪心算法，如下图，从最大的币值20开始 (因为20可以代替2张10,4张5或20张1)，不断地找回20，直到不够该币值时，往小的币值10，5，1依次遍历。

这里每一次都取的是最优值，最后的结果也达到了最优。
在这里插入图片描述

但局部最优一定能推导到全局最优吗？看下一个例子：

例子2 (局部最优不能到全局最优)：
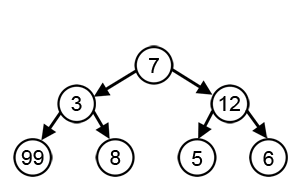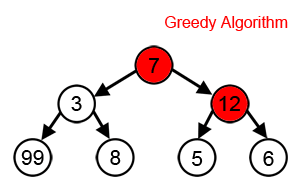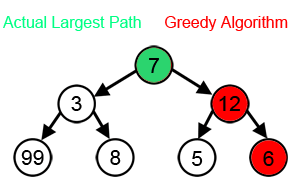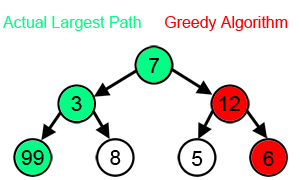
请添加图片描述
为了达到最大和，在每一步，贪心算法都会选择看起来是最优的直接选择，所以它会在第二步选择 12 而不是 3，并且不会达到包含 99 的最佳解决方案。

我们可以做出目前看起来最好的任何选择，即局部最优选择，然后解决以后出现的子问题。贪心算法做出的选择可能取决于到目前为止所做的选择，但不取决于未来的选择或子问题的所有解决方案。它迭代地做出一个又一个贪婪的选择，将每个给定的问题减少为一个较小的问题。

换句话说，贪心算法永远不会重新考虑它的选择，它是不可更改的，即我们无法在执行过程中的任何后续点更改决定。这是与动态规划的主要区别，动态规划是详尽的并且保证能找到解决方案。在每个阶段之后，动态规划都会根据前一阶段做出的所有决策做出下一步决策，并且可能会重新考虑前一阶段解决方案的算法路径。

贪心算法是独立每步最大，而动态规划是每一步之间状态关联最大，是个重叠子问题，这会在下一篇文章中讲解。

1.2、何时使用贪心

当遇到一道题，如何判别是否适合使用贪心算法？如何看出能从局部最优推导到全局最优？

贪心无套路，也没有框架之类的，需要多看多练培养感觉才能想到贪心的思路。

一般而言，就靠自己去手动模拟，即单纯的过程模拟，如果模拟可行，就试一试贪心策略，如果找出局部最优并可以推出全局最优，就是贪心，如果局部最优都没找出来，就不是贪心，可能是单纯的模拟；如果连模拟都不行，可能需要动态规划。

刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。

如果使用贪心算法，对于推导时，举例子得出的结论靠谱与否不确定，想要严格的数学证明。一般数学证明有如下两种方法：1. 数学归纳法，2. 反证法
但面试中基本不会让面试者现场证明贪心的合理性，代码写出来跑过测试用例即可，或者自己能自圆其说理由就行了。并且，贪心有时候就是常识性的推导，所以自然而然会认为本应该就这么做。

1.3、贪心算法的做题步骤

贪心算法一般分为如下四步：

将问题分解为若干个子问题
找出适合的贪心策略
求解每一个子问题的最优解
将局部最优解堆叠成全局最优解

这是一个细分，真正做题的时候很难分出这么详细的解题步骤，可能就是因为贪心的题目往往还和其他方面的知识混在一起。

二、经典题型

2.1、简单题目

2.1.1、455.分发饼干

力扣题目链接

在这里插入图片描述

这里的局部最优就是大饼干喂给胃口大的，充分利用饼干尺寸喂饱一个，全局最优就是喂饱尽可能多的小孩。

贪心算法1（以小孩的胃口为主体）：
先满足胃口大的孩子，需要排序后逆序

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        # 两个指针分别遍历两个list
        i, j = 0, 0
        # 存储结果
        count = 0
        # 排序，从胃口大的孩子开始满足
        g.sort(reverse=True)
        s.sort(reverse=True)

        # 从大遍历孩子和饼干
        # 孩子胃口过大，则换下一个胃口小的孩子
        while i<len(g) and j<len(s):
            # 匹配成功，都移到下一个匹配项
            if g[i]<=s[j]:
                count+=1
                i+=1
                j+=1
            # 匹配不成功，原因只有孩子胃口过大，因为饼干大于或等于胃口都满足匹配
            # 那么换下一个孩子
            else:
                i+=1
        return count

贪心算法2（以饼干为主体）：
排序后，饼干从小的开始分发，不满足则往后换大的

class Solution:
    def findContentChildren(self, g: List[int], s: List[int]) -> int:
        # 两个指针分别遍历两个list
        i, j = 0, 0
        # 存储结果
        count = 0
        # 排序，从小饼干开始分发
        g.sort()
        s.sort()

        # 从小遍历孩子和饼干
        # 饼干过小，换一个大一些的饼干
        while i<len(g) and j<len(s):
            # 匹配成功，都移到下一个匹配项
            if g[i]<=s[j]:
                count+=1
                i+=1
                j+=1
            # 匹配不成功，原因只有饼干太小
            # 那么换下一个饼干
            else:
                j+=1
        return count

在这里插入图片描述

2.1.2、1005.K次取反后最大化的数组和

力扣题目链接

贪心的思路，局部最优：让绝对值大的负数变为正数，当前数值达到最大，整体最优：整个数组和达到最大。局部最优可以推出全局最优。

那么如果将负数都转变为正数了，K依然大于0，此时的问题是一个有序正整数序列，如何转变K次正负，让数组和达到最大。

那么又是一个贪心：局部最优：只找数值最小的正整数进行反转，当前数值可以达到最大（例如正整数数组{5, 3, 1}，反转1 得到-1 比反转5得到的-5 大多了），全局最优：整个数组和达到最大。

这里注意有两次贪婪算法。

贪心算法1（一次排序，绝对值排序）：
解题步骤为：
第一步：将数组按照绝对值大小从大到小排序，注意要按照绝对值的大小
第二步：从前向后遍历，遇到负数将其变为正数，同时K–
第三步：如果K还大于0，那么反复转变数值最小的元素，将K用完
第四步：求和

class Solution:
    def largestSumAfterKNegations(self, A: List[int], K: int) -> int:
        A = sorted(A, key=abs, reverse=True) # 将A按绝对值从大到小排列
        for i in range(len(A)):
            if K > 0 and A[i] < 0:
                A[i] *= -1
                K -= 1
        if K > 0:
            A[-1] *= (-1)**K #取A最后一个数只需要写-1
        return sum(A)

贪心算法2（两次排序，直接排序）：

class Solution:
    def largestSumAfterKNegations(self, nums: List[int], k: int) -> int:
        nums.sort()
        

        count=0
        # 第一次贪婪，将负数变为正数，遍历列表一次
        while count<k and count<len(nums):
            # 负的变为正的
            if nums[count]<0:
                nums[count] = -nums[count]
                # 改变的次数计数
                count+=1
            # 排序后，遇到正的，退出，整个列表都为正的
            else:
                break

        # 第二次贪婪，偶数改变次数，则不变
        # 奇数改变次数，只变化最小值
        if (k-count)%2!=0:
            nums.sort()
            nums[0] = -nums[0]
            
        return sum(nums)

2.1.3、860.柠檬水找零

力扣题目链接

贪心算法：
仔细分析可知，这题只需要维护三种金额的数量，5，10和20就行，并且这题的判断条件非常少，有如下三种情况：
情况一：账单是5，直接收下。
情况二：账单是10，消耗一个5，增加一个10
情况三：账单是20，优先消耗一个10和一个5，如果不够，再消耗三个5

情况一，情况二，都是固定策略，不用具体分析了，而唯一不确定的就是情况三。情况三这里使用了贪心算法，优先使用大的币值10，因为5更加万能，如果对于交付20过多使用5找零，那么对于10的找零5就会相应的减少，同时存了很多10而用不掉。

class Solution:
    def lemonadeChange(self, bills: List[int]) -> bool:
        res = [0,0,0]

        for i in bills:
        	# 情况一
            if i == 5:
            	# 存钱
                res[0]+=1
            # 情况二
            elif i ==10:
            	# 存钱
                res[1]+=1
                # 判断钱是否够找零
                if res[0]<0:
                    return False
                # 找钱
                res[0]-=1
            # 情况三
            else:
                res[2]+=1
                # 先找大零钱，判断1
                if res[1]>=1 and res[0]>=1:
                    res[0]-=1
                    res[1]-=1
                # 大零钱不够，用小零钱，判断2
                elif res[0]>=3:
                    res[0]-=3
                # 都不够，无法找零
                else:
                    return False
        return True

注意： 这里其实可以去掉20的存取，因为不会用到。

2.2、中等题目1 - 序列问题

2.2.1、376. 摆动序列

力扣题目链接

改题使用贪心算法，相邻元素相减，一旦符号与前一个不同，则为摆动子序列

贪心算法：

class Solution:
    def wiggleMaxLength(self, nums: List[int]) -> int:
        # 单个元素也是摇摆序列，提前+1
        res= 1
        # 定义符号
        pre_sign = 0

        # 这里从1开始，每次跟前面的元素比较
        for i in range(1, len(nums)):
            # 这里符号0直接被考虑进去，相当于起始点，即一个元素
			# [0,0,2,1]第二个零当做起始点

            # 正向摆动，但前一个摆动符号不为正
            if nums[i]-nums[i-1]>0 and pre_sign<=0:
                pre_sign = 1
                res+=1
            # 负向摆动，但前一个摆动符号不为负
            elif nums[i]-nums[i-1]<0 and pre_sign>=0:
                pre_sign=-1
                res+=1
            
        return res

在这里插入图片描述

这道题，如果用贪心算法，有些找规律的意味在里面。

我们可以从上图看到，理论上，原本应该是1-17-5-15-5-16-8，即取低谷与峰值为判断条件才是合理的，然而对于像5-10-13-15-10-5这个从低谷到峰值中间都有值，从贪心的角度，我们直接判断，取第二个10当做峰值，同样达到效果，编程也更加方便。

动态规划：
子序列相关题目理论上可以使用动态规划算法，但是理解有些复杂，并且算法复杂度较高。目前先不做展开，后续补充。

2.2.2、738.单调递增的数字

力扣题目链接

贪心算法：

class Solution:
    def monotoneIncreasingDigits(self, n: int) -> int:
        tmp = list(str(n))
        
        for i in range(len(tmp)-1,0,-1):
            if int(tmp[i])<int(tmp[i-1]):
            	# 前一个值退一位
                tmp[i-1] = str(

最低0.47元/天解锁文章