Abaqus隐式求解和显式求解

Abaqus隐式求解和显式求解

1.隐式求解法

1.1隐式求解法的特点：

利用迭代求解下个增量步的未知量
无条件稳定，任何大小的增量皆可让结果在一定范围内
有计算收敛问题

1.2隐式求解法案例：

例如，将外力P分解成4个增量加载到结构上，结合初始劲度系数得到位移量σ1。但是根据节点内外力平衡来计算，0.25P的外力实际上没法带来σ1的位移量，因为随着节点下移，弹簧的劲度系数也在增加。这就带来了一个低估劲度系数而引起的残余值R1。

计算残余值R1反作用在节点带来的最终位移σ2。重复以上过程直到残差值符合我们的设定要求。

满足残差需求之后得到第一个增量结果Increment1并继续施加下一个增量之外力。

结果展示：
拆分为两个增量步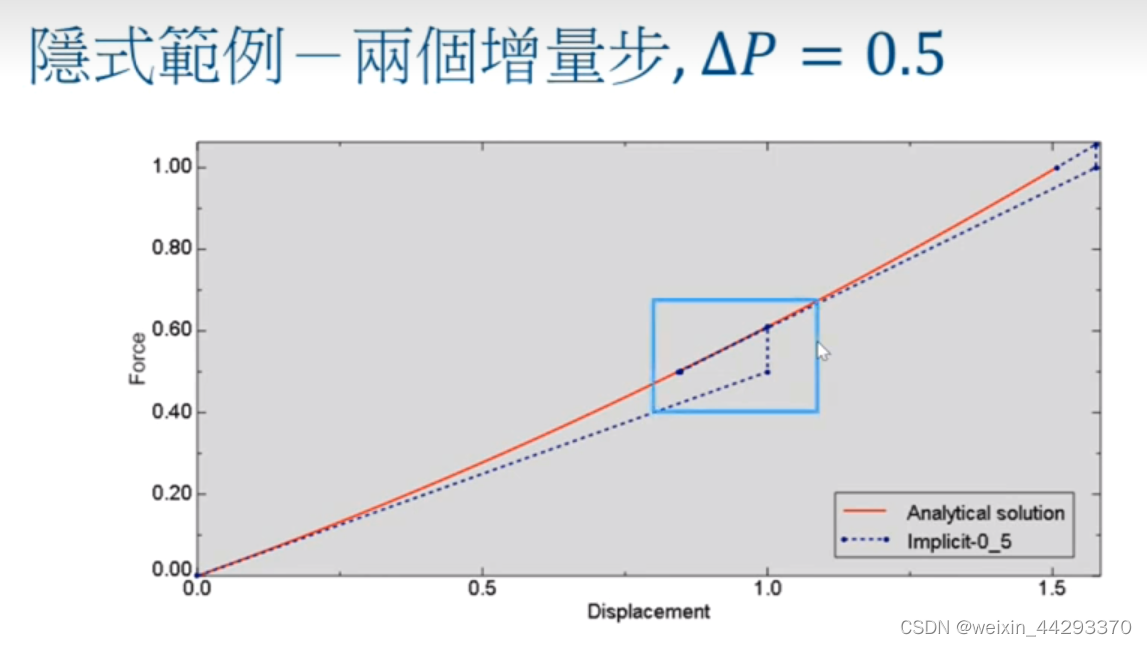
拆分为四个增量步

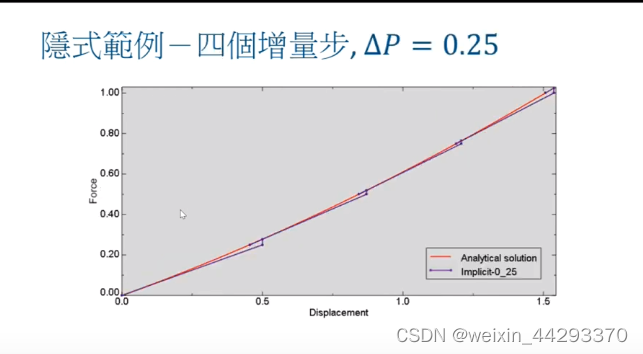
无论是拆分成两个，四个还是八个增量步，结果都是稳定的

2.显式求解法

2.1显式求解法的特点：

仅考虑前一时刻之状态
有条件稳定，增量必须小于一临界值，才会提供可靠结果
无计算收敛问题

2.2 显式求解法的案例

同样把外力分成四个增量加载到节点上，结合初始劲度系数，可以得到位移量σ1。此后不在考虑静力平衡的迭代过程，直接进行下一个增量步的计算

结果展示：
不同的增量步大小会带来不同的误差。误差是积累起来的。

2.3显式求解法的原理

显示求解法采用中心差分法来计算。可以发现，下一时刻的位移ui+1只和前面的状态有关，所以不需要考虑迭代收敛。

由此可见，显式求解法十分依赖中心差分的精度，这就要求时间增量不能太大，一般我们利用稳定时间增量来确定显示求解法增量步的数量级。





采用显式求解法建议打开双精度。

3.隐式求解法和显式求解法的对比