文章目录
A 正弦波振荡电路
A.a 正弦波振荡的条件和电路的组成
1 正弦波振荡的条件
无外加输入信号,依靠电路的自激振荡而产生正弦波输出电压的电路。
与负反馈放大电路的振荡的不同之处:在正弦波振荡电路中引入的是正反馈,且振荡频率可控。

在点扰动下,对于某一特定频率
f
0
f_0
f0(其他频率的信号仍然是负反馈,振荡越来越弱)的信号形成正反馈:

但是不会无限放大,因为放大电路中是晶体管、场效应管等非线性器件。由于半导体器件的非线性特性及供电电源的限制,最终达到动态平衡,稳定在一定的幅值。
起振与稳幅的过程
输出电压从幅值很小、含有丰富频率,到仅有一种频率且幅值由小逐渐增大直至稳幅。

一旦产生稳定的振荡,则电路的输出量自维持,即:

而负反馈放大电路自激幅值平衡条件为: A ˙ F ˙ = − 1 \dot{A}\dot{F}=-1 A˙F˙=−1
上面是平衡条件,如果是起振(刚通电时),则要求每一次反馈的信号幅值要大于前一次输入信号输入信号的幅值,这样输出幅值才能从无到有逐渐增大即:
要产生正弦波振荡,必须有满足相位条件的
f
0
f_0
f0,且在合闸通电时对于
f
=
f
0
f=f_0
f=f0信号有从小到大直至稳幅的过程,即满足起振幅值条件:
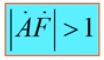
2 基本组成部分
(1)放大电路:放大作用
(2)正反馈网络:满足相位条件
(3)选频网络:确定
f
0
f_0
f0,保证电路产生正弦波振荡
(4)稳幅环节(通常利用非线性环节如晶体管等):稳幅。
通常(2)和(3)是合二为一的。
3 分析方法
(1)是否存在基本组成部分;
(2)放大电路是否正常工作,即是否有合适的Q点,信号是否正常传递,没有被短路或断路。
(3)是否满足相位条件,即是否存在
f
0
f_0
f0,使电路形成正反馈;
(4)是否满足幅值条件,即是否一定振荡(
∣
A
˙
F
˙
∣
>
1
→
∣
A
˙
F
˙
∣
=
1
|\dot{A}\dot{F}|>1\rightarrow |\dot{A}\dot{F}|=1
∣A˙F˙∣>1→∣A˙F˙∣=1)。
相位条件的判断方法:瞬时极性法
在多数正弦波振荡电路中,输出量、净输入量和反馈量均为电压量。
反馈量就是它的输入信号,把它断开,加上一个假设的输入信号。然后推出反馈信号的极性与假设的输入信号极性是否一致,如果一致,则把反馈信号取代输入信号,这样电路就可以振荡。(正反馈)。如果是相反的,则不会振荡(负反馈)。
总结:

断开反馈,在断开处给放大电路如
f
=
f
0
f=f_0
f=f0的信号
U
i
U_i
Ui,且规定其极性,然后根据

如果 U f U_f Uf和 U i U_i Ui极性相同,则电路可能产生自激振荡;否则电路不可能产生自激振荡。
4 分类
利用选频网络所用元件分类:
(1)RC正弦波振荡电路:1MHz以下
(2)LC正弦波振荡电路:1MHz以上
(3)石英晶体正弦波振荡电路:振荡频率稳定
A.b RC正弦波振荡电路
1 RC串并联选频网络

1 j w C \frac{1}{jwC} jwC1低频段并联部分C忽略不计,串联部分R忽略不计,变为高通电路。
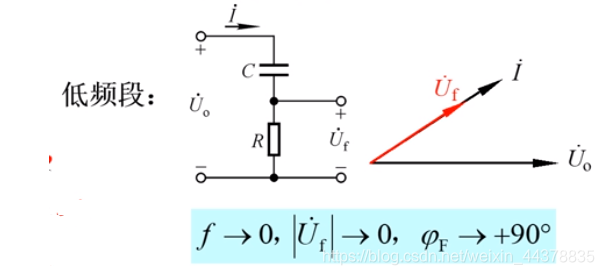
高频段,并联部分R忽略不计,串联部分C忽略不计,变为低通电路。

注意:低频段高通超前;高频端低通滞后。
在频率从 0 − ∞ 0 -\infty 0−∞中必有一个频率 f 0 f_0 f0, φ F = 0 \varphi_F=0 φF=0
RC串并联选频网络的频率响应

a:超前,高通;b:滞后,低通;
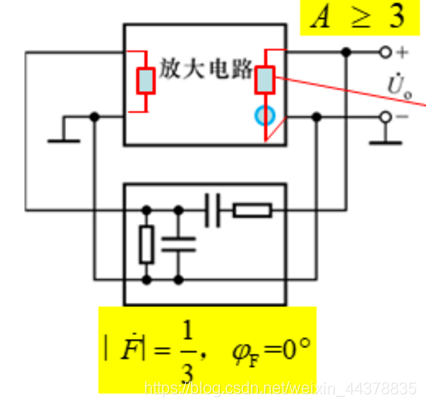
2 电路组成
A
F
>
1
,
F
=
1
/
3
,
A
>
=
3
AF>1,F=1/3,A>=3
AF>1,F=1/3,A>=3
放大电路
能否使用共射放大电路:否,输入输出反相,不符合相位条件。
能否使用共集放大电路:否,放大倍数小于1,不符合幅值条件;
能否使用共基放大电路:符合相位条件,幅值条件,但输入电阻小,输出电阻大,影响
f
o
f_o
fo:(基本放大电路输入电阻与反馈网络的电阻(左边的)并联,输出电阻与反馈网络的电阻串联(右边的)。)
要使振荡频率与放大电路无关,就应为RC串并联网络配一个电压放大倍数略大于3、输入电阻趋于无穷大、输出电阻趋于0的放大电路。
那么放大电路应该如何组成呢:可引入电压串联负反馈电路,使电压放大倍数大于3,且
R
i
R_i
Ri大、
R
o
R_o
Ro小,对
f
0
f_0
f0影响小。
3 RC桥式正弦波振荡电路(文氏桥振荡器)
用同相比例运算电路作为放大电路

A
=
U
o
U
p
=
1
+
R
f
R
1
≥
3
A=\frac{U_o}{U_p}=1+\frac{R_f}{R_1}\ge3
A=UpUo=1+R1Rf≥3得到:
R
f
≥
2
R
1
R_f\ge 2R_1
Rf≥2R1
因同相比例运算电路有非常好的线性度,故 R 1 R_1 R1(正比例系数)或 R f R_f Rf(负比例系数)可用热敏电阻( A = 1 + R f R 1 A=1+\frac{R_f}{R_1} A=1+R1Rf)。
或加二极管作为非线性环节:

动态信号下相当于一个电阻 r d = U T I d r_d=\frac{U_T}{I_d} rd=IdUT,温度T升高, U o U_o Uo增大, I d I_d Id增大 r d r_d rd减小。 A = 1 + R f + r d R 1 A=1+\frac{R_f+r_d}{R_1} A=1+R1Rf+rd减小。 U o U_o Uo为正, D 2 D_2 D2导通, U o U_o Uo为负, D 1 D_1 D1导通。
如果再加上稳压管:可以限制输出电压的峰-峰值。

f 0 = 1 2 π R C f_0=\frac{1}{2\pi RC} f0=2πRC1通常改变电容以粗调,改变电位器滑动端(代替R)以微调,实现频率可调。
合理连接电路,组成文氏桥振荡电路:

A.c LC正弦波振荡电路
LC正弦波振荡电路可产生1MHz以上的高频正弦波信号。由于一般运放频带较窄,而高速运放价格又比较昂贵,所以LC振荡电路中的放大器一般采用分立元件(分立元件是与集成电路(俗话说“芯片”)相对而言的,就是指普通的电阻、电容、晶体管等电子元件,统称分立元件)组成。按反馈方式的不同,可分为:

A.c.a LC并联网络的选频特性

图中电阻R为电感线圈的损耗。
低频时,电容的容抗要比电感容抗大得多,网络呈现电感的性质。
高频时,电感的感抗比电容感抗大得多,网络呈现电容的性质
当频率变化时,并联电路阻抗的大小和性质都发生变化。
并联电路的导纳:


(1)LC并联谐振频率


谐振回路的品质因数是用来评价回路损耗大小的指标。一般,Q值在几十到几百范围内。
LC并联回路的阻抗:
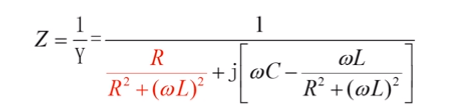
发生并联谐振时:
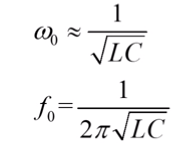
(2)并联谐振时回路的等效阻抗:
并联谐振时,等效阻抗为最大值。

可见,Q值不同,回路的阻抗不同。
(3)在
f
=
f
0
f=f_0
f=f0时,设输入电路为
I
0
I_0
I0,则电容和电感中电流为
Q
I
0
QI_0
QI0

(4)LC并联电路的幅频特性

相频特性:

当
f
=
f
0
f=f_0
f=f0时,电路为纯电阻性,等效阻抗最大;当
f
<
f
0
f<f_0
f<f0时,电路为感性;当
f
>
f
0
f>f_0
f>f0时,电路为容性。所以LC并联电路具有选频特性。

电路的品质因数越大,选频特性越好。
LC选频放大电路=>正弦波振荡电路

当
f
=
f
0
f=f_0
f=f0时,电压放大倍数的数值最大,且附加相移为0。

φ A = π ; φ A + φ F = 2 n π ; \varphi_A=\pi;\varphi_A+\varphi_F=2n\pi; φA=π;φA+φF=2nπ;反馈网络应能使得产生 π \pi π的相移。最简单的做法是引入变压器。
A.c.b 变压器反馈式电路

分析电路是否可能产生正弦波振荡的步骤:
(1)是否存在四个组成部分;
基本放大电路:Vcc,Rb2,Rb1,Re,Ce,T
选频:C,N1
反馈网络:N2
稳幅环节:三极管
(2)放大电路是否能正常工作【静态(画直流通路)、动态输入信号有没有被短路或者断路】
静态:
U
B
Q
=
U
c
c
R
b
1
+
R
b
2
R
b
1
U_{BQ}=\frac{U_{cc}}{R_{b1}+R_{b2}}R_{b1}
UBQ=Rb1+Rb2UccRb1;
I E Q = U B Q − U B E R e I_{EQ}=\frac{U_{BQ}-U_{BE}}{R_e} IEQ=ReUBQ−UBE
U
C
E
Q
=
V
c
c
−
U
R
e
U_{CEQ}=V_{cc}-U_{Re}
UCEQ=Vcc−URe
动态:
f
0
=
1
2
π
L
C
f_0=\frac{1}{2\pi\sqrt{LC}}
f0=2πLC1一般为1兆赫兹,因此C很小,交流下不可短路。而C1和Ce交流下视为短路。
(3)是否满足相位条件(是否为正反馈)
必须要有合适的同铭端。
将反馈端断开,在断开与地之间加入一个输入信号(频率为
f
0
f_0
f0)。在判断其他的极性。

反馈端的极性应与假设的输入信号相同(正反馈)。标出同铭端(红点)
(4)是否可能满足幅值条件(|AF|>=1)
特点:易振,波形较好;耦合不紧密,损耗大,频率稳定性不高。
为使N1、N2耦合紧密,将它们合二为一,组成电感反馈式电路。
A.c.c 电感反馈式电路

反馈电压取自N2。
C1必须要,否则在静态时基极与集电极电压相同,管子无法处于放大状态。
交流通路:

电感的三个抽头分别接晶体管的三个极,故称之为电感三点式电路。
f 0 = 1 2 π L ′ C f_0=\frac{1}{2\pi\sqrt{L'C}} f0=2πL′C1,其中, L ′ = L 1 + L 2 + 2 m L'=L1+L2+2m L′=L1+L2+2m
特点:耦合紧密,易振,振幅大,C用可调电容可获得较宽范围的振荡频率(电感扎数难改变)。波形较差,常含有高次谐波。
因为放大电路的输入电阻就是它自身的负载,故
A
˙
\dot{A}
A˙与
F
˙
\dot{F}
F˙具有相关性;若增大
N
1
N_1
N1,则
∣
A
˙
∣
|\dot{A}|
∣A˙∣增大,
∣
F
˙
∣
|\dot{F}|
∣F˙∣减小。
由于电感对高频信号呈现较大的电抗,故波形中含高次谐波,为使谐波波形好,采用电容反馈式电路。
A.c.d 电容反馈式(电容三点式)电路

反馈电压取自C2
C2极性判断:C1是上为负,下为正;C1C2所在回路在并联谐振时受外电路影响几乎为0,故为串联关系。,故C2极性为上负下正。符合正反馈。

若要振荡频率高,则L、C1、C2的取值就要小。当电容减小到一定程度时,晶体管的极间电容将并联在C1和C2上,影响振荡频率。
可在L所在回路串联一电容。


特点:波形好,振荡频率调整范围小,适用于频率固定的场合。
讨论:
变压器反馈式电路:

共基所以T集电极为正;反馈要求N2上正下负,才是正反馈。CI为耦合电容,Cb为旁路电容。
电感容三点式:

电感三点式:

A.d 石英晶体正弦波振荡电路
1 石英晶体的特点

S
i
O
2
SiO_2
SiO2结晶体按一定方向切割的晶片。
压电效应和压电振荡:机械变形和电场的关系。固有频率只决定于其几何形状,故非常稳定。
等效电路:

一般LC选频网络的Q为几百,石英晶体的Q可达到
1
0
4
1
0
6
10^4~10^6
104 106;前者
Δ
f
/
f
\Delta f/f
Δf/f
1
0
−
5
10^{-5}
10−5,后者可达到
1
0
−
10
−
1
0
−
11
10^{-10}-10^{-11}
10−10−10−11
2 电路
并联型电路:

石英晶体工作在感性区,构成电感反馈式。
串联型电路:

石英晶体两端同相,工作在电阻区








 本文深入探讨正弦波振荡电路的工作原理,包括正弦波振荡的条件、电路组成、分析方法及分类。重点讲解RC、LC正弦波振荡电路,石英晶体振荡电路的特性和应用,以及电路的选频、反馈和稳幅机制。
本文深入探讨正弦波振荡电路的工作原理,包括正弦波振荡的条件、电路组成、分析方法及分类。重点讲解RC、LC正弦波振荡电路,石英晶体振荡电路的特性和应用,以及电路的选频、反馈和稳幅机制。

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










