【机器学习的数学基础】（十）向量微积分(Vector Calculus)(下)

5 向量微积分(Vector Calculus)(下)

5.4 矩阵的梯度

我们会遇到这样的情况：我们需要求矩阵关于向量（或其他矩阵）的梯度，最后得到多维的张量( tensor，我们可以把张量看作一个多维数组。)。我们可以把这一张量看作是一个元素为偏导数的多维数组。例如，如果我们计算$m\times n$矩阵$\mathbf{A}$相对于$p\times q$矩阵$\mathbf{B}$的梯度，得到的雅可比矩阵的形状将是$（m\times n）\times （p\times q）$，即一个四维张量$\mathbf{J}$，其各个元素表示为$J_{ijkl}=\partial A_{ij}/\partial B_{kl}$。

由于矩阵表示线性映射，我们可以利用$m\times n$矩阵的空间${\mathbb{R}}^{m\times n}$和$mn$向量的空间${\mathbb{R}}^{mn}$之间存在向量空间同构（线性可逆映射）的事实，将两个矩阵重塑(re-shape)成长度分别为$mn$和$pq$的向量。然后使用这些向量计算梯度，得到大小为$mn\times pq$的雅可比矩阵。

考虑计算矩阵$\mathbf{A}\in {\mathbb{R}}^{4\times 2}$相对于向量$\mathbf{x}\in {\mathbb{R}}^3$的梯度计算。我们知道梯度的维度为$\frac{\mathrm{d}\mathbf{A}}{\mathrm{d}\mathbf{x}}\in {\mathbb{R}}^{4\times 2\times 3}$。下面给出两种求梯度的方法。

方法1

我们计算偏导数$\frac{\partial \mathbf{A}}{\partial x_1},\frac{\partial \mathbf{A}}{\partial x_2},\frac{\partial \mathbf{A}}{\partial x_3}$，得到每个偏导数都是$4\times 2$的矩阵，把它们集合成$4\times 2\times 3$的矩阵。

方法2

我们把$\mathbf{A}\in {\mathbb{R}}^{4\times 2}$重塑（re-shape (flatten)） 成一个向量$\tilde{\mathbf{A}}\in {\mathbb{R}}^8$。然后我们计算$\frac{\mathrm{d}\tilde{A}}{\mathrm{d}\mathbf{x}}\in {\mathbb{R}}^{8\times 3}$。最后再通过重塑这个梯度得到梯度张量，如图所示。

例 5.12 向量相对于矩阵的梯度

已知：
$$\begin{array}{ll}\mathbf{f}=\mathbf{A}\mathbf{x},& \mathbf{f}\in {\mathbb{R}}^M,\mathbf{A}\in {\mathbb{R}}^{M\times N},\mathbf{x}\in {\mathbb{R}}^N\end{array}$$
求梯度：$\mathrm{d}\mathbf{f}/\mathrm{d}\mathbf{A}$。

让我们从确定梯度的维数开始
$$\frac{\mathrm{d}\mathbf{f}}{\mathrm{d}\mathbf{A}}\in {\mathbb{R}}^{M\times (M\times N)}$$
根据定义，梯度是偏导数的集合：
$$\frac{\mathrm{d}\mathbf{f}}{\mathrm{d}\mathbf{A}}=\left[\begin{array}{c}\frac{\partial f_1}{\partial \mathbf{A}}\\ ⋮\\ \frac{\partial f_M}{\partial \mathbf{A}}\end{array}\right],\frac{\partial f_i}{\partial \mathbf{A}}\in {\mathbb{R}}^{1\times (M\times N)}$$

显式写出矩阵向量乘法将对我们计算偏导数有帮助：
$$f_i=\sum _{j=1}^N{A}_{ij}{x}_j,i=1,\dots ,M$$
其偏导数如下所示
$$\frac{\partial f_i}{\partial A_{iq}}=x_q$$
这允许我们计算$f_i$对$\mathbf{A}$各行的偏导数，如下所示
$$\frac{\partial f_i}{\partial A_{i,:}}={\mathbf{x}}^{\top }\in {\mathbb{R}}^{1\times 1\times N}$$
$$\frac{\partial f_i}{\partial A_{k\ne i,:}}=0^{\top }\in {\mathbb{R}}^{1\times 1\times N}$$

在这里我们必须注意维度是否正确。由于$f_i$映射到$\mathbb{R}$上，且$\mathbf{A}$的每一行的大小为$1\times N$，因此我们得到一个$1\times 1\times N$大小的张量，作为$f_i$对$\mathbf{A}$的每一行的偏导数。

我们将$\mathbf{A}$对每一行的偏导数叠加在一起，得到我们想要的梯度：
$$\frac{\partial f_i}{\partial \mathbf{A}}=\left[\begin{array}{c}{0}^{\top }\\ ⋮\\ 0^{\top }\\ {\mathbf{x}}^{\top }\\ 0^{\top }\\ ⋮\\ 0^{\top }\end{array}\right]\in {\mathbb{R}}^{1\times (M\times N)}$$

例 5.13 矩阵相对于矩阵的梯度

考虑矩阵$\mathbf{R}\in {\mathbb{R}}^{M\times N}$和$\mathbf{f}:{\mathbb{R}}^{M\times N}\to {\mathbb{R}}^{N\times N}$，且有：
$$\mathbf{f}(\mathbf{R})={\mathbf{R}}^{\top }\mathbf{R}=:\mathbf{K}\in {\mathbb{R}}^{N\times N}$$
求梯度$\mathrm{d}\mathbf{K}/\mathrm{d}\mathbf{R}$

为了解决这个难题，让我们先写下我们已经知道的：梯度是一个张量且维数(把$\mathbf{R}$划分为列向量，然后用前文的方法一来分析会比较清晰)为：
$$\frac{\mathrm{d}\mathbf{K}}{\mathrm{d}\mathbf{R}}\in {\mathbb{R}}^{(N\times N)\times (M\times N)}(5.94)$$

且对于$p,q=1,\dots ,N$：
$$\frac{\mathrm{d}{K}_{pq}}{\mathrm{d}\mathbf{R}}\in {\mathbb{R}}^{1\times M\times N}$$
其中$K_{pq}$为$\mathbf{K}=\mathbf{f}(\mathbf{R})$的在$(p,q)$上的元素。用${\mathbf{r}}_i$表示$\mathbf{R}$的第$i$列，$\mathbf{K}$的每一项都是$\mathbf{R}$的两列的点积，即：
$$K_{pq}={\mathbf{r}}_p^{\top }{\mathbf{r}}_q=\sum _{m=1}^M{R}_{mp}{R}_{mq}$$
现在我们计算偏微分$\frac{\partial K_{pq}}{\partial R_{ij}}$，我们得到：
$$\frac{\partial K_{pq}}{\partial R_{ij}}=\sum _{m=1}^M\frac{\partial }{\partial R_{ij}}{R}_{mp}{R}_{mq}={\partial }_{pqij}$$

$${\partial }_{pqij}=\{\begin{array}{ll}{R}_{iq}& \text{ if }j=p,p\ne q\\ R_{ip}& \text{ if }j=q,p\ne q\\ 2R_{iq}& \text{ if }j=p,p=q\\ 0& \text{ otherwise }\end{array}(5.98)$$
从 (5.94)可知我们期望的梯度维度为$(N\times N)\times (M\times N)$，且这个张量的各个元素有(5.98)的${\partial }_{pqij}$给出，其中$p,q,j=1,\dots ,N$，$i=1,\dots ,M$。

5.5 计算梯度的有用恒等式

下面，我们列出了机器学习中经常需要的一些有用的梯度 (Petersen and Pedersen, 2012)。这里，我们使用$\mathrm{tr}(\cdot )$作为迹（见定义4.4），$\det (\cdot )$作为行列式（见第4.1节），假设$\mathbf{f}(\mathbf{X})$的倒数存在，为$\mathbf{f}(\mathbf{X}{)}^{-1}$。
$$\frac{\partial }{\partial \mathbf{X}}\mathbf{f}(\mathbf{X}{)}^{\top }={\left(\frac{\partial \mathbf{f}(\mathbf{X})}{\partial \mathbf{X}}\right)}^{\top }（5.99）$$
$$\frac{\partial }{\partial \mathbf{X}}\mathrm{tr}(\mathbf{f}(\mathbf{X}))=\mathrm{tr}\left(\frac{\partial \mathbf{f}(\mathbf{X})}{\partial \mathbf{X}}\right)$$
$$\frac{\partial }{\partial \mathbf{X}}\det (\mathbf{f}(\mathbf{X}))=\det (\mathbf{f}(\mathbf{X}))\mathrm{tr}\left(\mathbf{f}(\mathbf{X}{)}^{-1}\frac{\partial \mathbf{f}(\mathbf{X})}{\partial \mathbf{X}}\right)$$
$$\frac{\partial {\mathbf{a}}^{\top }{\mathbf{X}}^{-1}\mathbf{b}}{\partial \mathbf{X}}=-{\left({\mathbf{X}}^{-1}\right)}^{\top }\mathbf{a}{\mathbf{b}}^{\top }{\left({\mathbf{X}}^{-1}\right)}^{\top }（5.102)$$
$$\frac{\partial {\mathbf{x}}^{\top }\mathbf{a}}{\partial \mathbf{x}}={\mathbf{a}}^{\top }$$
$$\frac{\partial {\mathbf{a}}^{\top }\mathbf{x}}{\partial \mathbf{x}}={\mathbf{a}}^{\top }$$
$$\frac{\partial {\mathbf{a}}^{\top }\mathbf{X}\mathbf{b}}{\partial \mathbf{X}}=\mathbf{a}{\mathbf{b}}^{\top }$$

$$\frac{\partial {\mathbf{x}}^{\top }\mathbf{B}\mathbf{x}}{\partial \mathbf{x}}={\mathbf{x}}^{\top }\left(\mathbf{B}+{\mathbf{B}}^{\top }\right)$$

对于对称矩阵$\mathbf{W}$
$$\frac{\partial }{\partial \mathbf{s}}(\mathbf{x}-\mathbf{A}\mathbf{s}{)}^{\top }\mathbf{W}(\mathbf{x}-\mathbf{A}\mathbf{s})=-2(\mathbf{x}-\mathbf{A}\mathbf{s}{)}^{\top }\mathbf{W}\mathbf{A}$$

备注：
在这本书中，我们只讨论了矩阵的迹和转置。然而，我们已经看到导数的对象可以是高维的张量，在这种情况下，一般的迹和转置是没有定义的。在这种情况下，$D\times D\times E\times F$张量的迹是$E\times F$维矩阵。这是张量收缩的一个特例。类似地，当我们“转置”张量时，则交换它的前两个维度。具体来说，（5.99）到（5.102），当我们处理多元函数$\mathbf{f}(\cdot )$和计算矩阵的导数时，我们需要进行张量相关的特殊计算（并选择不进行如第5.4节所述都向量化）。

5.6 反向传播与自动微分法

在许多机器学习应用中，我们通过执行梯度下降（第7.1节）来找到好的模型参数，这基于我们可以计算目标函数相对于模型参数的梯度。对于给定的目标函数，我们可以通过微积分和应用链式法则来获得关于模型参数的梯度；见第5.2.2节。在第5.3节中，我们已经研究了线性回归模型的平方损失函数的梯度。

考虑函数
$$f(x)=\sqrt{x^2+\exp \left(x^2\right)}+\cos \left(x^2+\exp \left(x^2\right)\right)(5.109)$$

通过应用链式法则，我们可以计算梯度：
$$\frac{\mathrm{d}f}{\mathrm{d}x}=\frac{2x+2x\exp \left(x^2\right)}{2\sqrt{x^2+\exp \left(x^2\right)}}-\sin \left(x^2+\exp \left(x^2\right)\right)\left(2x+2x\exp \left(x^2\right)\right)$$
$$=2x\left(\frac{1}{2\sqrt{x^2+\exp \left(x^2\right)}}-\sin \left(x^2+\exp \left(x^2\right)\right)\right)\left(1+\exp \left(x^2\right)\right)(5.110)$$
以这种方式写出梯度通常是不切实际的，因为它常常导致导数的表达式非常冗长。在实践中意味着梯度的实现可能比计算函数值还要更多的计算开销。对于训练深度神经网络模型，反向传播( backpropagation)算法((Kelley, 1960; Bryson, 1961; Dreyfus, 1962; Rumelhart et al., 1986)是计算误差函数相对于模型参数的梯度的有效方法。

5.6.1 深度网络中的梯度

链式法则被发挥到极致的一个领域是深度学习，其中函数值$\mathbf{y}$为多级函数组合
$$\mathbf{y}=\left(f_K\circ f_{K-1}\circ \cdots \circ f_1\right)(\mathbf{x})=f_K\left(f_{K-1}\left(\cdots \left(f_1(\mathbf{x})\right)\cdots \right)\right)$$
其中$\mathbf{x}$为输入（例如：图像），$\mathbf{y}$为观测值（例如：类别标签），且每一个$f_i,i=1,\dots ,K$都拥有自己的参数。

在多层神经网络中，我们在第$i$层有函数$f_i\left({\mathbf{x}}_{i-1}\right)=\sigma \left({\mathbf{A}}_{i-1}{\mathbf{x}}_{i-1}+{\mathbf{b}}_{i-1}\right)$。这里${\mathbf{x}}_{i-1}$是第$i-1$层的输出而$\sigma$为激活函数，激活函数可以是logistic sigmoid $\frac{1}{1+e^{-x}}$、tanh或rectified linear unit (ReLU)等。为了训练这些模型，我们需要求损失函数$L$对于所有模型参数${\mathbf{A}}_j$，${\mathbf{b}}_j$的梯度，其中$j=1,\dots ,K$。这也要求我们计算$L$相对于每层输入的梯度。例如，如果我们有输入$\mathbf{x}$和观测值$\mathbf{y}$，则网络结构由以下定义：
$${\mathbf{f}}_0:=\mathbf{x}$$
$${\mathbf{f}}_i:={\sigma }_i\left({\mathbf{A}}_{i-1}{\mathbf{f}}_{i-1}+{\mathbf{b}}_{i-1}\right),i=1,\dots ,K$$
将其可视化如图5.8所示。

图5.8多层神经网络的前向传递，计算$\mathbf{x}$作为输入，${\mathbf{A}}_i,{\mathbf{b}}_i$参数的函数$\mathbf{L}$的损失。

我们目的是找到${\mathbf{A}}_j,{\mathbf{b}}_j，j=0,\dots ,K-1$，使得平方损失：
$$L(\mathbf{\theta })={\Vert \mathbf{y}-{\mathbf{f}}_K(\mathbf{\theta },\mathbf{x})\Vert }^2$$
最小。其中： θ = { A 0 , b 0 , … , A K − 1 , b K − 1 } \boldsymbol{\theta}=\left\{\boldsymbol{A}_{0}, \boldsymbol{b}_{0}, \ldots, \boldsymbol{A}_{K-1}, \boldsymbol{b}_{K-1}\right\} θ={A0​,b0​,…,AK−1​,bK−1​}。

为了得到关于参数集$\mathbf{\theta }$的梯度，我们需要计算$L$对于每层参数 θ j = { A j , b j } ， j = 0 , … , K − 1 \boldsymbol{\theta}_{j}=\left\{\boldsymbol{A}_{j}, \boldsymbol{b}_{j}\right\}，j=0, \ldots, K-1 θj​={Aj​,bj​}，j=0,…,K−1的偏导数。链式法则允许我们确定偏导数为：

橙色项是每一层的输出相对其输入的偏导数，而蓝色项是每一层的输出相对于其参数的偏导数。假设我们已经计算了偏导数$\partial L/\partial {\mathbf{\theta }}_{i+1}$，那么大部分的计算结果可以被重用来计算$\partial L/\partial {\mathbf{\theta }}_i$。我们将需要另外计算的附加项用方框表示。图5.9展示了梯度通过网络向后传递。

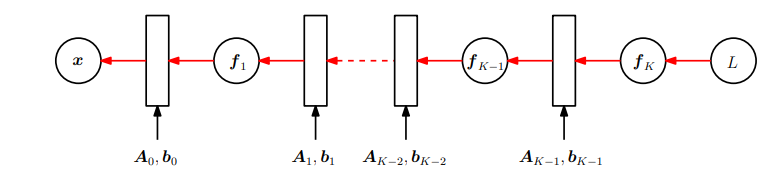
图 5.9多层神经网络反向传播计算损失函数的梯度。

5.6.2 自动微分

其实，反向传播是数值分析中称为自动微分(automatic differentiation)技术的一个特例。我们可以把自动微分看作是一套技术，它通过处理中间变量和应用链式法则，在数值上（而不是符号化地）计算函数的精确（达到机器精度）梯度。自动微分应用了一系列基本算术运算，例如加法和乘法，以及基本函数，例如：$\sin ,\cos ,\exp ,\log$。将链式法则应用到这些运算中，可以自动计算相当复杂函数的梯度。自动微分适用于一般的计算机程序，有正向和反向两种模式。Baydin等人（2018年）对机器学习中的自动微分进行了很好的概述。

图 5.10一个简单的图，说明了通过中间变量$a,b$的从$x$到$y$的数据流。

图 5.10显示了一个简单的图，表示输入$x$通过一些中间变量$a、b$到输出$y$的数据流。如果我们要计算导数$\mathrm{d}y/\mathrm{d}x$，我们应用链式法则可得到：
$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}b}\frac{\mathrm{d}b}{\mathrm{d}a}\frac{\mathrm{d}a}{\mathrm{d}x}$$

直观地说，正向和反向模式在乘法的顺序上是不同的。由于矩阵乘法的结合性，我们有以下两种选择：
$$\frac{\mathrm{d}y}{\mathrm{d}x}=\left(\frac{\mathrm{d}y}{\mathrm{d}b}\frac{\mathrm{d}b}{\mathrm{d}a}\right)\frac{\mathrm{d}a}{\mathrm{d}x}(5.120)$$
$$\frac{\mathrm{d}y}{\mathrm{d}x}=\frac{\mathrm{d}y}{\mathrm{d}b}\left(\frac{\mathrm{d}b}{\mathrm{d}a}\frac{\mathrm{d}a}{\mathrm{d}x}\right)(5.121)$$

方程（5.120）是反向模式( reverse mode)，因为梯度通过数据流向后传播。方程（5.121）是正向模式(forward mode)，其中梯度随数据从左到右流过整个图。

下面，我们将重点介绍反向模式的自动微分，即反向传播。在神经网络中，输入的维数通常比标签的维数高得多，所以反向模式比正向模式计算量要少得多。让我们从一个例子开始。

例 5.14

考虑函数：
$$f(x)=\sqrt{x^2+\exp \left(x^2\right)}+\cos \left(x^2+\exp \left(x^2\right)\right)(5.109)$$
如果我们在计算机上实现一个函数$f$，我们可以通过以下中间变量(intermediate variables)来节省一些计算量：
$$\begin{array}{l}a=x^2\\ b=\exp (a)\\ c=a+b\\ d=\sqrt{c}\\ e=\cos (c)\\ f=d+e\end{array}$$

这与应用链式法则时的思维过程是相同的。注意，前面的方程组需要的运算比(5.109)直接定义函数$f(x)$少。图5.11显示了要获得函数值$f$所需的数据流和计算。

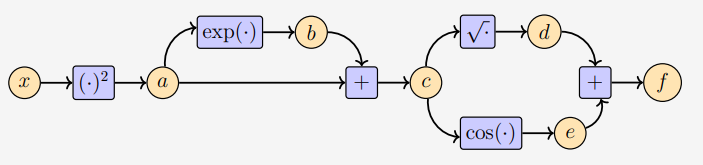
图 5.11 输入$x$，函数值f和中间变量$a,b,c,d,e$的计算图。

包含中间变量的方程组可以看作是一个计算图，这是一种广泛用于实现神经网络软件库的表示。通过调用定义的初等函数导数，我们可以直接计算中间变量对其相应输入的导数。我们得到以下结果：
$$\frac{\partial a}{\partial x}=2x$$
$$\frac{\partial b}{\partial a}=\exp (a)$$
$$\frac{\partial c}{\partial a}=1=\frac{\partial c}{\partial b}$$
$$\frac{\partial d}{\partial c}=\frac{1}{2\sqrt{c}}$$
$$\frac{\partial e}{\partial c}=-\sin (c)$$
$$\frac{\partial f}{\partial d}=1=\frac{\partial f}{\partial e}$$

通过查看计算图，我们可以从输出向后计算$\partial f/\partial x$：
$$\frac{\partial f}{\partial c}=\frac{\partial f}{\partial d}\frac{\partial d}{\partial c}+\frac{\partial f}{\partial e}\frac{\partial e}{\partial c}$$
$$\frac{\partial f}{\partial b}=\frac{\partial f}{\partial c}\frac{\partial c}{\partial b}$$
$$\frac{\partial f}{\partial a}=\frac{\partial f}{\partial b}\frac{\partial b}{\partial a}+\frac{\partial f}{\partial c}\frac{\partial c}{\partial a}$$
$$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial a}\frac{\partial a}{\partial x}$$

注意，我们隐式地应用链式规则来获得$\partial f/\partial x$。通过替换初等函数导数的结果，我们得到
$$\frac{\partial f}{\partial c}=1\cdot \frac{1}{2\sqrt{c}}+1\cdot (-\sin (c))$$
$$\frac{\partial f}{\partial b}=\frac{\partial f}{\partial c}\cdot 1$$
$$\frac{\partial f}{\partial a}=\frac{\partial f}{\partial b}\exp (a)+\frac{\partial f}{\partial c}\cdot 1$$
$$\frac{\partial f}{\partial x}=\frac{\partial f}{\partial a}\cdot 2x$$

通过将上述每一个导数看作一个变量，我们观察到计算导数所需的计算与函数本身的计算具有相似的复杂度。这是非常反直觉的，要知道导数$\frac{\partial f}{\partial x}$的数学表达式（5.110）比（5.109）中函数$f(x)$的数学表达式要复杂得多。

自动微分是示例5.14的形式化。令$x_1,\dots ,x_d$是函数的输入变量，$x_{d+1},\dots ,x_{D-1}$为中间变量，$x_D$为输出变量。那么计算图可以表示为：
$$\text{ For }i=d+1,\dots ,D:x_i=g_i\left(x_{\mathrm{Pa}\left(x_i\right)}\right)（5.143）$$

其中$g_i(\cdot )$是初等函数，$x_{\mathrm{P}\mathrm{a}\left(x_i\right)}$是图中变量$x_i$的父节点。给定一个这样定义的函数，我们可以用链式法则一步一步地计算函数的导数。我们定义$f=x_D$，那么有：
$$\frac{\partial f}{\partial x_D}=1$$
对于其他变量$x_i$，我们应用链式法则：
$$\frac{\partial f}{\partial x_i}=\sum _{x_j:x_i\in \mathrm{Pa}\left(x_j\right)}\frac{\partial f}{\partial x_j}\frac{\partial x_j}{\partial x_i}=\sum _{x_j:x_i\in \mathrm{Pa}\left(x_j\right)}\frac{\partial f}{\partial x_j}\frac{\partial g_j}{\partial x_i}（5.145）$$

其中$\mathrm{Pa}\left(x_j\right)$是计算图中$x_j$的父节点集。方程（5.143）是函数的正向传播，而（5.145）是梯度,它通过计算图的反向传播梯度。对于神经网络训练，我们将相对于标签的预测误差进行反向传播。

当我们有一个可以表示为计算图的函数，且它的各个元素函数是可微的时，上面的自动微分方法就能起作用。实际上，这个函数甚至可以不是一个数学函数，而是一个计算机程序。然而，并不是所有的计算机程序都能被求微分，例如在我们找不到关于它的微分初等函数的情况。对于for循环和if语句这样的编程结构，也需要注意。

5.7 高阶导数

到目前为止，我们已经讨论了梯度，即一阶导数。有时，我们对高阶导数感兴趣，例如，当我们想使用牛顿法进行优化时，需要二阶导数（Nocedal和Wright，2006）。在第5.1.1节中，我们讨论了用多项式逼近函数的泰勒级数。在多变量的情况下，我们可以做完全相同的事情。让我们从定义一些符号开始。

考虑有两个变量$x,y$的函数$f:{\mathbb{R}}^2\to \mathbb{R}$。对于高阶偏导数（和梯度），我们使用以下表示法：

• $\frac{{\partial }^{2}f}{\partial x^2}$为$f$关于$x$的二阶偏导。
• $\frac{{\partial }^{n}f}{\partial x^n}$为$f$关于$x$的$n$阶偏导。
• $\frac{{\partial }^{2}f}{\partial y\partial x}=\frac{\partial }{\partial y}\left(\frac{\partial f}{\partial x}\right)$为$f$先对$x$求偏微分，然后对$y$求偏微分得到的偏导数。
• $\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{\partial }{\partial x}\left(\frac{\partial f}{\partial y}\right)$为$f$先对$y$求偏微分，然后对$x$求偏微分得到的偏导数。

Hessian矩阵由所有二阶偏导数的组成。

如果$f(x，y)$是两次（连续）可微函数，那么
$$\frac{{\partial }^{2}f}{\partial x\partial y}=\frac{{\partial }^{2}f}{\partial y\partial x}$$

也就是说，微分的次序并不重要，相应的Hessian矩阵为
$$\mathbf{H}=\left[\begin{array}{cc}\frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial x\partial y}\\ \frac{{\partial }^{2}f}{\partial x\partial y}& \frac{{\partial }^{2}f}{\partial y^2}\end{array}\right]$$

它是对称的。Hessian矩阵被表示为：${\nabla }_{x,y}^{2}f(x,y)$。一般地，对于$\mathbf{x}\in {\mathbb{R}}^n$和$f:{\mathbb{R}}^n\to \mathbb{R}$，Hessian矩阵是$n\times n$矩阵。Hessian矩阵度量函数在$(x,y)$附近的局部曲率。

备注： 向量场的Hessian函数

如果$f:{\mathbb{R}}^n\to {\mathbb{R}}^m$为向量场，则其对应的Hessian函数是一个$(m\times n\times n)$的张量。

5.8 线性化与多元泰勒级数

函数$f$的梯度$\nabla f$经常用于${\mathbf{x}}_0$附近的局部线性近似
$$f(\mathbf{x})\approx f\left({\mathbf{x}}_0\right)+\left({\nabla }_{\mathbf{x}}f\right)\left({\mathbf{x}}_0\right)\left(\mathbf{x}-{\mathbf{x}}_0\right)（5.148）$$
这里$\left({\nabla }_{\mathbf{x}}f\right)\left({\mathbf{x}}_0\right)$为$f$相对于$\mathbf{x}$的梯度并用${\mathbf{x}}_0$代入计算。

图 5.12函数的线性近似。使用一阶泰勒级数展开来将原始函数$f$在$x_0=-2$处线性化。

图 5.12展示了输入${\mathbf{x}}_0$处函数$f$的线性近似。原始函数被一条直线近似。这个近似值是局部精确的，即离${\mathbf{x}}_0$越远，近似值就越不精确。方程（5.148）是$f$在${\mathbf{x}}_0$处的多变量泰勒级数展开的特例，这里我们只考虑前两项。我们将在下面讨论更一般的情况，这将达到更好的近似。

定义 5.7多变量泰勒级数

我们考虑函数：
$$\begin{array}{rl}f:{\mathbb{R}}^D& \to \mathbb{R}\\ & \mathbf{x}\mapsto f(\mathbf{x}),\mathbf{x}\in {\mathbb{R}}^D\end{array}$$
在${\mathbf{x}}_0$处光滑。当我们定义差分向量$\mathbf{\delta }:=\mathbf{x}-{\mathbf{x}}_0$，则$f$在${\mathbf{x}}_0$的多变量泰勒级数( multivariate Taylor series)为：
$$f(\mathbf{x})=\sum _{k=0}^{\infty }\frac{D_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right)}{k!}{\mathbf{\delta }}^k（5.151）$$

式中，$D_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right)$是$f$对$\mathbf{x}$的第$k$阶导数，并在${\mathbf{x}}_0$处求值

定义 5.8 泰勒多项式

${\mathbf{x}}_0$处$f$的$n$次泰勒多项式包含（5.151）中级数的前$n+1$个分量，定义为
$$T_n(\mathbf{x})=\sum _{k=0}^n\frac{D_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right)}{k!}{\mathbf{\delta }}^k（5.152）$$

在（5.151）和（5.152）中，我们使用了略微粗略的${\mathbf{\delta }}^k$表示法，这对于$\mathbf{x}\in {\mathbb{R}}^D,D>1$和$k>1$情况下是无定义的。

要注意，$D_{\mathbf{x}}^{k}f$和${\mathbf{\delta }}^k$都是$k$阶张量，即$k$维数组。$k$阶张量${\mathbf{\delta }}^k\in {\mathbb{R}}^{\stackrel{k\text{ times }}{\overbrace{D\times D\times \dots \times D}}}$由$\mathbf{\delta }\in {\mathbb{R}}^D$的$k$倍外积(表示为$\otimes$)得到。例如：
$${\mathbf{\delta }}^2:=\mathbf{\delta }\otimes \mathbf{\delta }=\mathbf{\delta }{\mathbf{\delta }}^{\top },{\mathbf{\delta }}^2[i,j]=\delta [i]\delta [j]$$

$${\mathbf{\delta }}^3:=\mathbf{\delta }\otimes \mathbf{\delta }\otimes \mathbf{\delta },{\mathbf{\delta }}^3[i,j,k]=\delta [i]\delta [j]\delta [k]$$

一般来说，我们可以得到泰勒级数中的项：
$$D_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^k=\sum _{i_1=1}^D\cdots \sum _{i_k=1}^D{D}_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right)\left[i_1,\dots ,i_k\right]\delta \left[i_1\right]\cdots \delta \left[i_k\right]$$

其中$D_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^k$包含$k$阶多项式。

现在我们定义了向量场的泰勒级数，让我们显式地写出泰勒级数展开式的第一项$D_{\mathbf{x}}^{k}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^k$，其中$k=0,\dots ,3$和$\mathbf{\delta }:=\mathbf{x}-{\mathbf{x}}_0$

$$k=0:D_x^{0}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^0=f\left({\mathbf{x}}_0\right)\in \mathbb{R}$$
$$k=1:D_{\mathbf{x}}^{1}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^1=\underset{1\times D}{\underbrace{{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0\right)}}\underset{D\times 1}{\underbrace{\mathbf{\delta }}}=\sum _{i=1}^D{\nabla }_{\mathbf{x}}f\left({\mathbf{x}}_0\right)[i]\delta [i]\in \mathbb{R}$$
$$\begin{array}{rl}k& =2:D_{\mathbf{x}}^{2}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^2=\mathrm{tr}(\underset{D\times D}{\underbrace{\mathbf{H}\left({\mathbf{x}}_0\right)}}\underset{D\times 1}{\underbrace{\mathbf{\delta }}}\underset{1\times D}{\underbrace{{\mathbf{\delta }}^{\top }}})={\mathbf{\delta }}^{\top }\mathbf{H}\left({\mathbf{x}}_0\right)\mathbf{\delta }\\ & =\sum _{i=1}^D\sum _{j=1}^{D}H[i,j]\delta [i]\delta [j]\in \mathbb{R}\end{array}$$
$$k=3:D_x^{3}f\left({\mathbf{x}}_0\right){\mathbf{\delta }}^3=\sum _{i=1}^D\sum _{j=1}^D\sum _{k=1}^D{D}_x^{3}f\left({\mathbf{x}}_0\right)[i,j,k]\delta [i]\delta [j]\delta [k]\in \mathbb{R}$$
其中${\mathbf{H}}_{{\mathbf{x}}_0}$为$f$在${\mathbf{x}}_0$的Hessian矩阵

例 5.15 双变量函数的泰勒级数展开

考虑函数：
$$f(x,y)=x^2+2xy+y^3（5.161）$$
我们要计算$f$在$\left(x_0,y_0\right)=(1,2)$时的泰勒级数展开式。在开始之前，让我们先讨论一下期望的结果：（5.161）中的函数是一个3次多项式，它本身就是多项式的线性组合。因此，我们不需要泰勒级数展开包含四阶或更高阶的项。这意味着，对于（5.161）的精确表示，只需确定（5.151）的前四项就足够了。

为了确定泰勒级数展开式，我们从常数项和一阶导数开始，它们由
$$f(1,2)=13$$
$$\frac{\partial f}{\partial x}=2x+2y⟹\frac{\partial f}{\partial x}(1,2)=6$$
$$\frac{\partial f}{\partial y}=2x+3y^2⟹\frac{\partial f}{\partial y}(1,2)=14$$
因此，我们得到：
$$D_{x,y}^{1}f(1,2)={\nabla }_{x,y}f(1,2)=\left[\frac{\partial f}{\partial x}(1,2)\frac{\partial f}{\partial y}(1,2)\right]=\left[\begin{array}{ll}6& 14\end{array}\right]\in {\mathbb{R}}^{1\times 2}$$
它使得：
$$\frac{D_{x,y}^{1}f(1,2)}{1!}\mathbf{\delta }=\left[\begin{array}{ll}6& 14\end{array}\right]\left[\begin{array}{l}x-1\\ y-2\end{array}\right]=6(x-1)+14(y-2)$$

注意$D_{x,y}^{1}f(1,2)\mathbf{\delta }$只包含线性项，即一阶多项式

二阶偏导数由下式给出
$$\frac{{\partial }^{2}f}{\partial x^2}=2⟹\frac{{\partial }^{2}f}{\partial x^2}(1,2)=2$$
$$\frac{{\partial }^{2}f}{\partial y^2}=6y⟹\frac{{\partial }^{2}f}{\partial y^2}(1,2)=12$$
$$\frac{{\partial }^{2}f}{\partial y\partial x}=2⟹\frac{{\partial }^{2}f}{\partial y\partial x}(1,2)=2$$
$$\frac{{\partial }^{2}f}{\partial x\partial y}=2⟹\frac{{\partial }^{2}f}{\partial x\partial y}(1,2)=2$$

当我们收集二阶偏导数时，我们得到了Hessian函数
$$\mathbf{H}=\left[\begin{array}{cc}\frac{{\partial }^{2}f}{\partial x^2}& \frac{{\partial }^{2}f}{\partial x\partial y}\\ \frac{{\partial }^{2}f}{\partial y\partial x}& \frac{{\partial }^{2}f}{\partial y^2}\end{array}\right]=\left[\begin{array}{cc}2& 2\\ 2& 6y\end{array}\right]（5.171）$$

使得：
$$\mathbf{H}(1,2)=\left[\begin{array}{cc}2& 2\\ 2& 12\end{array}\right]\in {\mathbb{R}}^{2\times 2}$$
因此，泰勒级数展开式的下一项由以下给出
$$\begin{array}{rl}\frac{D_{x,y}^{2}f(1,2)}{2!}{\mathbf{\delta }}^2& =\frac{1}{2}{\mathbf{\delta }}^{\top }\mathbf{H}(1,2)\mathbf{\delta }\\ & =\frac{1}{2}\left[\begin{array}{ll}x-1& y-2\end{array}\right]\left[\begin{array}{cc}2& 2\\ 2& 12\end{array}\right]\left[\begin{array}{l}x-1\\ y-2\end{array}\right]\\ & =(x-1{)}^2+2(x-1)(y-2)+6(y-2{)}^2.\end{array}$$

这里，$D_{x,y}^{2}f(1,2){\mathbf{\delta }}^2$只包含二次项，即二阶多项式

三阶导数如下所示：
$$D_{x,y}^{3}f=\left[\begin{array}{ll}\frac{\partial H}{\partial x}& \frac{\partial H}{\partial y}\end{array}\right]\in {\mathbb{R}}^{2\times 2\times 2}$$
$$D_{x,y}^{3}f[:,:,1]=\frac{\partial \mathbf{H}}{\partial x}=\left[\begin{array}{cc}\frac{{\partial }^{3}f}{\partial x^3}& \frac{{\partial }^{3}f}{\partial x^2\partial y}\\ \frac{{\partial }^{3}f}{\partial x\partial y\partial x}& \frac{{\partial }^{3}f}{\partial x\partial y^2}\end{array}\right]$$
$$D_{x,y}^{3}f[:,:,2]=\frac{\partial \mathbf{H}}{\partial y}=\left[\begin{array}{cc}\frac{{\partial }^{3}f}{\partial y\partial x^2}& \frac{{\partial }^{3}f}{\partial y\partial x\partial y}\\ \frac{{\partial }^{3}f}{\partial y^2\partial x}& \frac{{\partial }^{3}f}{\partial y^3}\end{array}\right]$$

由于Hessian方程（5.171）中的大多数二阶偏导数是常数，因此非零的三阶偏导数只有：
$$\frac{{\partial }^{3}f}{\partial y^3}=6⟹\frac{{\partial }^{3}f}{\partial y^3}(1,2)=6$$

高阶导数和3阶混合导数（如$\frac{\partial f^3}{\partial x^2\partial y}$）都被消去，因此
$$D_{x,y}^{3}f[:,:,1]=\left[\begin{array}{cc}0& 0\\ 0& 0\end{array}\right],D_{x,y}^{3}f[:,:,2]=\left[\begin{array}{ll}0& 0\\ 0& 6\end{array}\right]$$
则有：
$$\frac{D_{x,y}^{3}f(1,2)}{3!}{\mathbf{\delta }}^3=(y-2{)}^3$$

它收集了泰勒级数的所有三次项。总的来说，$f$在$\left(x_0,y_0\right)=(1,2)$处的（精确）泰勒级数展开式是

在这种情况下，我们得到了（5.161）中多项式的精确泰勒级数展开式，即（5.180c）中的多项式与（5.161）中的原多项式相同。在这个特殊的例子中，这个结果并不让人惊讶，因为原始函数仅仅是一个三阶多项式，我们在（5.180c）中通过常数项、一阶、二阶和三阶多项式的线性组合即可表示它。

翻译自：
《MATHEMATICS FOR MACHINE LEARNING》作者是 Marc Peter Deisenroth，A Aldo Faisal 和 Cheng Soon Ong

公众号后台回复【m4ml】即可获取这本书。

另外，机器学习的数学基础.pdf