数据结构第一天

最新推荐文章于 2024-05-16 16:43:57 发布

原创最新推荐文章于 2024-05-16 16:43:57 发布 · 266 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#数据结构

数据结构专栏收录该内容

6 篇文章

订阅专栏

绪论

1 时间复杂度
2 timeit模块
3 算法与数据结构的区别

由于之前学过数据结构，因此今天的学习，主要是复习，笔记只记录学到的新知识。

1 时间复杂度

（1）单靠运行时间衡量算法效率未必可靠

为完成同一功能编写了两个不同的程序，其中一个放在古老的计算机上运行，另外一个放在一台性能优越的机器上运行，这样的话，根据运行时间来比较两个程序的优劣，就显得不客观。程序的运行离不开计算机环境（包括硬件和操作系统），这些因素会影响程序运行的速度并反应在程序的执行时间上。

（2）时间复杂度的概念

我们假定计算机执行算法每一个基本操作的时间是固定的一个时间单位，那么有多少个基本操作就代表会花费多少时间单位。同一个算法，在不同的计算机上，其基本操作数是相同的，也就是说，我们可以使用算法执行所需要的基本操作次数，来评价算法的效率。
算法执行所需要的基本操作总次数，可以用 f(n) 来表示，n 表示问题的规模。我们一般只考虑算法基本操作次数的数量级，也就是说，在算法分析的时候，认为 3n 和 100n +50 属于同一个量级，忽略常量因子（即 3n 中的 3，100n +50 中的100和50）。
若一个算法中，基本操作的总次数是 f(n)，那么其时间复杂度可记为 T(n) = O(f(n))，此即为“大O记法”。
观察下面例子，理解一下“大O记法”

如果 f(n) = c, c 为与 n 无关的常数，那么时间复杂度为 T(n)=O(f(n))=O(1)
如果 f(n) = a*n+b, a 和 b 为与n 无关的常数，那么时间复杂度为 T(n)=O(f(n))=O(n)
如果 f(n) = a*n^2 + b*n + c, a,b,c 均为常数，那么时间复杂度为 T(n)=O(f(n))=O(n^2), 只看次数最大的那一项
如果 f(n) = a*n + log n, a 为常数,  T(n)=O(f(n))=O(n)

析算法时，存在几种可能的考虑：
算法完成工作最少需要多少基本操作，即最优时间复杂度
算法完成工作最多需要多少基本操作，即最坏时间复杂度
算法完成工作平均需要多少基本操作，即平均时间复杂度

对于最优时间复杂度，其价值不大，因为它没有提供什么有用信息，其反映的只是最乐观最理想的情况，没有参考价值。

对于最坏时间复杂度，提供了一种保证，表明算法在此种程度的基本操作中一定能完成工作。

对于平均时间复杂度，是对算法的一个全面评价，因此它完整全面的反映了这个算法的性质。但另一方面，这种衡量并没有保证，不是每个计算都能在这个基本操作内完成。而且，对于平均情况的计算，也会因为应用算法的实例分布可能并不均匀而难以计算。

因此，我们主要关注算法的最坏情况，亦即最坏时间复杂度。

（3）常见的时间复杂度

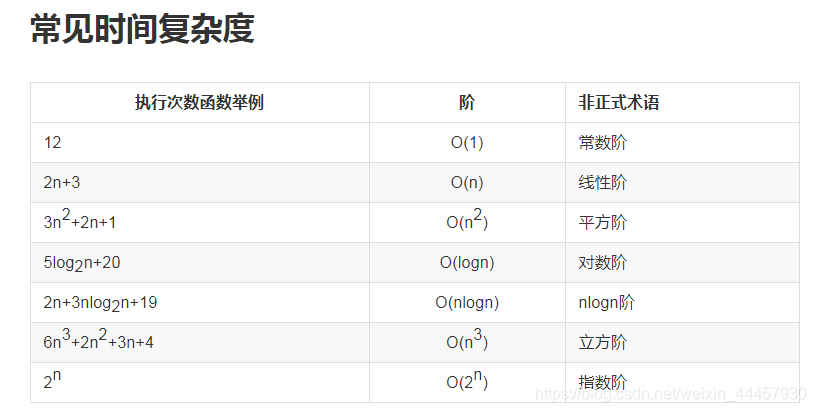
在这里插入图片描述

（4）时间复杂度的比较

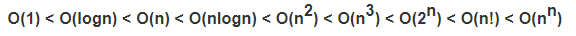
在这里插入图片描述
时间复杂度的比较，和高等数学里面“当 n 趋于无穷大时，无穷大的比较”是一样的。

（5）时间复杂度的几条基本计算规则

1.基本操作，即只有常数项，认为其时间复杂度为O(1)
2.顺序结构，时间复杂度按加法进行计算
3.循环结构，时间复杂度按乘法进行计算
4.分支结构，时间复杂度取最大值
判断一个算法的效率时，往往只需要关注操作数量的最高次项，其它次要项和常数项可以忽略
在没有特殊说明时，我们所分析的算法的时间复杂度都是指最坏时间复杂度

2 timeit模块

常用该模块来测试一小段Python代码的执行速度。

class timeit.Timer(stmt='pass', setup='pass', timer=<timer function>)

Timer是测量小段代码执行速度的类，stmt参数是要测试的代码语句（statment），setup参数是运行代码时需要的设置（比如，要完成对“stmt”语句的测算，需要导入什么东西），timer参数是一个定时器函数，与平台有关，该参数无需理会。

timeit.Timer.timeit(number=1000000)

Timer类中测试语句执行速度的对象方法。number参数是测试代码时的测试次数，默认为1000000次。方法返回执行代码的平均耗时，一个float类型的秒数，也就是说，返回的是对 stmt 测算一百万次后的平均运行时间。

def test1():
   l = []
   for i in range(1000):
      l = l + [i]
def test2():
   l = []
   for i in range(1000):
      l.append(i)
def test3():
   l = [i for i in range(1000)]     # 列表推导式
def test4():
   l = list(range(1000))
def test5():
    l = []
    for i in range(1000):
        l.extend([i])

from timeit import Timer

t1 = Timer("test1()", "from __main__ import test1")
# 两个参数都必须是字符串，第二个参数的意思是，从当前的模块中导入 test1，方便在其他地方进行运算，具体的暂时不深究
print("加号（+）拼接 ",t1.timeit(number=1000), "seconds")

t2 = Timer("test2()", "from __main__ import test2")
print("append ",t2.timeit(number=1000), "seconds")

t3 = Timer("test3()", "from __main__ import test3")
print("列表推导式 ",t3.timeit(number=1000), "seconds")

t4 = Timer("test4()", "from __main__ import test4")
print("list(range对象)",t4.timeit(number=1000), "seconds")

t5 = Timer("test5()", "from __main__ import test5")
print("extend ",t5.timeit(number=1000), "seconds")

输出

加号（+）拼接  6.138830099000001 seconds
append  0.23588022299999967 seconds
列表推导式  0.11678225300000022 seconds
list(range对象) 0.039543373999999964 seconds
extend  0.3418870159999994 seconds

从上面的运行结果来看，列表操作尽量少用加号（+），如果要使用拼接，可以用 extend

在设置的时候，也有可能是导入变量，如

from timeit import Timer
x = list(range(2000000))
pop_zero = Timer("x.pop(0)","from __main__ import x")
print("pop_zero ",pop_zero.timeit(number=1000), "seconds")
x = list(range(2000000))
pop_end = Timer("x.pop()","from __main__ import x")
print("pop_end ",pop_end.timeit(number=1000), "seconds")

输出

pop_zero  3.676260248 seconds
pop_end  0.00028823600000027483 seconds

这里需要注意的是，函数调用不是一个基本步骤，比如对列表 a 进行插入操作 a.insert(i, 100)，该操作的时间复杂度是O(n)。因为函数是将很多基本步骤进行封装，因此函数调用不是一个基本步骤，时间复杂度未必是O(1)。

3 算法与数据结构的区别

数据结构只是静态的描述了数据元素之间的关系，高效的程序需要在数据结构的基础上设计和选择算法。
程序 = 数据结构 + 算法

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体