论文阅读 Langdon2023 A unifying perspective on neural manifolds and circuits for cognition

月棹星舟

已于 2023-12-17 14:02:21 修改

阅读量1k

点赞数 25

分类专栏：神经科学论文阅读文章标签：论文阅读

于 2023-12-17 13:59:44 首次发布

本文链接：https://blog.csdn.net/weixin_44497127/article/details/135044048

版权

神经科学论文阅读专栏收录该内容

4 篇文章

订阅专栏

Langdon2023 A unifying perspective on neural manifolds and circuits for cognition

摘要

两种不同的观点为解释大脑和行为之间的联系提供了依据。一种方法试图寻找执行特定功能的神经电路组件，强调神经元之间的连接作为神经计算的基础。另一种方法以神经流形（神经群体活动中行为信号的低维表示）为中心，并表明神经计算是通过动力学涌现现象实现的。尽管神经流形揭示了异质神经元活动中可解释的结构，但在连接性中找到相应的结构仍然是一个挑战。我们重点介绍了一些例子，在这些例子中，建立低维活动和连通性之间的对应关系是可能的，从而统一了神经流形和神经电路的观点。这种关系在神经反应的几何拓扑反映其在大脑中空间布局的系统中很明显，例如飞行导航系统。此外，我们描述了有证据证明在异质性神经反应系统中，神经电路通过低秩连接性在囊括了流形上的活动模式之间的相互作用。我们认为，如果我们要能够因果地测试行为背后的神经计算理论，那么统一流形和电路方法是很重要的。

背景

研究神经连接结构如何产生神经动力学和行为活动是系统神经科学的核心目标。高通量记录可以记录越来越多的数据，但这些实验产生的观测数据并没有明确指出电路机制。同样，解剖学连接的重建限制可能的神经动力学空间，但不能唯一地预测由回路产生的活动模式来控制特定行为。因此，理论和计算建模有助于弥合电路连接、神经动力学和行为功能之间的差距

Circuit–manifold convergence: head direction system(头朝向系统)

头朝向的环形吸引子
头部方向角是一个一维圆形变量，在拓扑上等价于一个环。 bump 在圆圈内的位置精确地跟踪了苍蝇的实际头部方向，随其旋转而移动，并相对于 visual landmarks 进行调整。此外，在任何给定时间都只存在一个活动的 bump ，并且当光遗传学刺激诱导另一个人工bump 时，现有的活动bump 消失，bump 的独热特性及其随角速度的运动共同确立了ring manifold 的功能意义。
环吸引子模型
Continue ring attractor model: 由于局部循环激励，活动bump 可以自维持，并且由于全局抑制（即始终仅存在一个bump）而具有独热特性。

Towards convergence in grid cells（网格细胞）

空间位置的 toroidal manifold
通过流形分析研究结构
toroidal manifold 的电路机制
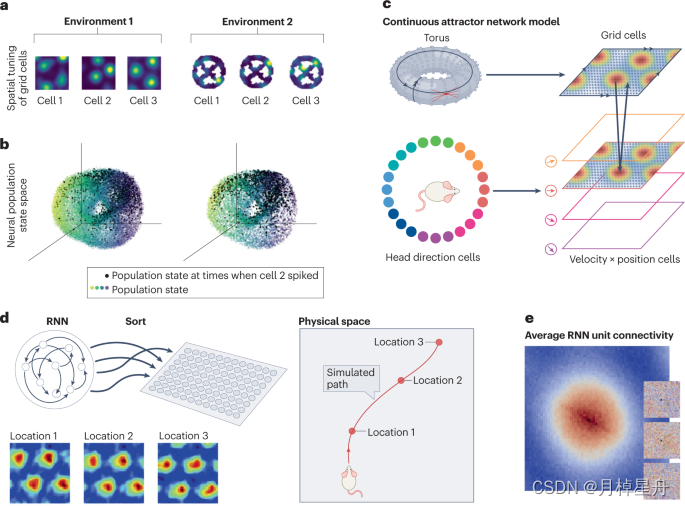
介绍了一种二维环的连续吸引子模型，单元在空间上排列在二维圆环上，单元之间循环兴奋连接的强度与将它们之间的距离成比例地减小。模型中单个或多个活动凸起以与种群中共活性网格细胞的位置相对应的空间模式自组织形成，与MEC中网格细胞的拓扑组织一致。此段指出：在没有直接连接性测量的情况下，可以通过在将稀疏神经记录与全局扰动策略相结合的实验中测试其预测预测输出来评估模型。
复杂网络种涌现的电路机制
例举了在针对路径积分的任务中，RNN单元（多个单元平均计算）可以涌现出存在局部激发和全局抑制的结构。

Circuits with mixed selectivity

与导航系统相比，神经流形和电路连接之间的关系在支持认知功能（如工作记忆或决策）的高级皮层区域中更加难以捉摸。但用于研究动物实验中认知功能的任务通常具有简单的拓扑结构。

认知任务的经典电路模型

例举了视觉空间工作记忆任务（要求动物记住刺激在屏幕上圆形的特定角度的位置）的建模工作。连续吸引子模型可以预测了记忆报告的精度与PFC活性波动之间的关系。以及复 winner take all competition的模型等。
认知任务的神经流形

例举有研究工作记忆任务中只有相对较小的部分（5-10%）PFC神经元表现出严格的持续活动，单个神经元表现出混合选择性，响应多个任务变量的组合，并且这些变量的编码分布在整个神经元群体中。而流形分析可以解决在具有分布式混合选择性的网络中理解神经计算原理的问题。
结合神经流行与神经连接

设计非线性高维 RNN 可以综和流形和神经连接。其中低维流形上的动力学来自低维连通性。低维动力系统隐藏在高维网络中。嵌入矩阵 Q 提供了潜伏电路和高维网络之间的映射，使得潜在节点 i 映射到向量 q(i)。两个隐节点之间的连接映射到高维分布式连接模式，该模式由沿流形的对应向量的外积给出。这种映射使我们能够将活动和连接的扰动从低维电路转换为高维网络，从而可以对电路机制进行因果测试。