机器学习--决策树

最新推荐文章于 2024-07-13 22:36:10 发布

Jahree

最新推荐文章于 2024-07-13 22:36:10 发布

阅读量254

点赞数

文章标签：数据挖掘机器学习 python 决策树算法

本文链接：https://blog.csdn.net/weixin_44504402/article/details/105779125

版权

文章目录

知识要点

信息熵

（1）概念
信息熵，在1948年由香农提出。用来描述系统信息量的不确定度。不确定性越大，则信息熵越大，反之，信息熵越小。
（2）计算方式
假设随机变量X具有m个值，分别为： $V_1,V_2,...,V_m$
且
$P（X=V_1）= p_1$
$P（X=V_2）= p_2$
…
$P（X=V_m）= p_m$
并且：
$p_1+p_2+...+p_m=1$
则变量X的信息期望值（信息熵）为：
$H(X)=-p_1*log_2p_1-p_2*log_2p_2-...-p_m*log_2p_m=-\sum_{i=1}^mp_ilog_2p_i$

（3）概率分布与信息熵
对于信息熵，我们可以用概率分布来衡量，对于随机变量X，其分布越均衡，则不确定性越多，信息熵越大。其分布越不均衡，则不确定性越小，信息熵越小。通过代码展现如下：

import numpy as np
import matplotlib.pyplot as plt

plt.rcParams["font.family"] = "SimHei" 
plt.rcParams["axes.unicode_minus"] = False 
plt.rcParams["font.size"] = 12

# 假设随机变量X可以取两个值，一个值的概率为p，则另外一个值的概率为1 - p。 
p = np.linspace(0.01, 0.99, 100)
# 计算在不同概率分布下的信息熵。
h = -p * np.log2(p) - (1 - p) * np.log2(1 - p)
plt.plot(p, h) 
plt.xlabel("p1取值") 
plt.ylabel("信息熵") 
plt.title("概率-信息熵对比") 
plt.show()

在这里插入图片描述
我们把概率分布转换到数据集上。信息熵体现的就是数据的不纯度，即样本类别的均衡程度。样本类别越均衡，不纯度越高，信息熵越大。反之，样本类别越不均衡，不纯度越低，信息熵越小。

决策树原理

决策树概念

决策树是一种树形结构，通过特征的不同来将样本数据划分到不同的分支（子树）中，最终，每个样本一定会划分到一个叶子结点中。我们可以将每个特征视为一个提问，特征值的不同，就视为样本给出的不同答案，然后，我们就可以根据一系列提问（特征），将样本划分到不同的叶子结点中。决策树是一种非参数监督学习方法，可以用于分类与回归。

训练决策树

给定如下数据集
在这里插入图片描述

我们可以将三个特征作为问题，依次来“询问”数据集中的每个样本，经过每个样本依次“作答”之后，就可以将样本划分到不同的分支中，这样，决策树就训练完成。其实，决策树的训练，就是根据训练集去构建一棵决策树。如图所示：
在这里插入图片描述

预测原理

当在训练集上构建决策树后，我们就可以对未知样本进行预测。预测的过程为：预测的过程为：根据未知的样本的特征，逐步进行分支选择（回答问题），直到叶子结点为止。那么，我们就可以使用该叶子结点中的已知样本来预测该未知样本。可是，我们预测的依据是什么呢？

对于分类树，使用叶子结点中类别数量最多的类别作为未知样本的类别。
对于回归树，使用叶子结点中所有样本的均值，作为未知样本的类别。

分类决策树

信息增益

信息增益（IG-Information Gain）定义如下：
$IG(D_p,f)=I(D_p)-\sum_{j=1}^n\frac{N_j}{N_p}I(D_j)$

$f$ ：划分的特征
$D_p$ ：父节点，即使用特征 $f$ 分割之前的节点
$IG(D_p,f)$ ：父节点 $D_p$ 使用特征 $f$ 划分下，获得的信息增益
$D_j$ ：父节点 $D_p$ 经过分割之后，会产生n个节点， $D_j$ 为第j个子节点
$N_p$ ：父节点 $D_p$ 包含样本的数量
$N_j$ ：第j个子节点 $D_j$ 包含的样本数量
$I$ ：不纯度度量标准

出于简化与缩小组合搜索空间的考虑，很多库（包括scikit-learn）实现的都是二叉决策树时，信息增益定义为：
$IG(D_p,f)=I(D_p)-\frac{N_l}{N_p}I(D_l)-\frac{N_r}{N_p}I(D_r)$

通过定义我们可知，信息增益就是父节点的不纯度减去所有子节点的不纯度（加权）

在选择特征分裂样本时，我们应该让子节点的不纯度尽可能的低，这样就可以更快的完成训练（更少的分割次数），同时，在预测未知样本是，也会具有更高的准确度。

训练规则

训练分类决策树的具体规则如下：
1.将每个特征看成是一种分裂可能。特征可以分为离散型和连续型。

对于离散型特征，每个类别可以划分为一个子节点（多叉树），或者属于类别A与不属于类别A（二叉树）
对于连续型特征，可以划分为大于等于A与小于A

2.从根节点开始，选择可获得最大信息增益的特征进行分裂（实现信息增益最大化）
3.对子节点继续选择能够获得最大信息增益的特征进行分裂，知道满足如下条件之一，停止分裂。

所有叶子节点中的样本属于同一类别
树达到指定的最大深度（max_depth），每一次分裂视为一层
叶子节点包含的样本数量小于指定的最小分裂样本数量（min_samples_split）
如果分裂后，叶子节点包含的样本数量小于指定的叶子最小样本数量（min_samples_leaf）

不纯度度量标准

不纯度可以采用如下方式度量：

信息熵
基尼系数
错误率

信息熵

$I_H(D)=-\sum_{j=1}^mp(i|D)log_2p(i|D)$

m：节点D中含有样本的类别数量
$p (i ∣ D)$ ：节点D中，属于类别i的样本占节点D中样本总数的比例（概率）

基尼系数

$I_G(D)=1-\sum_{j=1}^mp(i|D)^2$

错误率

$I_E(D)=1-max\lbrace p(i|D) \rbrace$

无论哪种度量标准，都有一个特性：如果样本以相同的比例分布于不同的类别是，度量值最大，不纯度最高。如果所有样本都属于同一个类别，则度量值为0，不纯度最低。

决策树算法

决策树主要包含以下三种算法：

ID3
C4.5
CART（classification and regression tree）

ID3

ID3（iterative dichotomiser 3）算法是非常经典的决策树算法，该算法描述如下：

使用多叉树
使用信息熵作为不纯度度量标准，选择信息增益最大的特征分割数据

ID3算法简单，训练较快，但算法有一些局限性，如下：

不支持连续特征
不支持缺失值
仅支持分类，不支持回归
在选择特征时，会倾向于选择类别多的特征

C4.5

C4.5算法是在ID3算法上改进而来，改算法描述如下：

使用多叉树结果
仅支持分类，不支持回归。

不过C4.5在ID3算法上进行了一些优化，包括：

支持对缺失值的处理
支持将连续值进行离散化处理
使用信息熵作为不纯度度量标准，但选择信息增益率（而不是信息增益）最大的特征分裂节点

信息增益率的定义为：
$IG_r(D_p,f)=\frac{IG_H(D_p,f)}{I_H(f)}$

$I_H(f)$ ：根据特征f的不同类别值比例，计算得到的信息熵。

之所以从信息增益改用信息增益率，是因为在ID3算法中，倾向于选择类别多的特征，因此，经过这样的调整，在C4.5中就可以得到缓解。因为类别多的特征在计算信息熵 $I_H(f)$ 时，往往会比类别少的特征信息熵大，这样，就可以在分母上进行一定的惩罚。

CART

CART，分类与回归树，该算法描述如下：

使用二叉树结构
支持连续值与缺失值处理
既支持分类，也支持回归。
（1）使用基尼系数作为不纯度度量标准，选择信息增益最大的特征分裂节点（分类）
（2）使用MSE或MAE最小的特征分类节点（回归）

程序实现

在scikit-learn中，使用优化的CART算法来实现决策树

分类

在scikit-learn中，提供DecisionTreeClassifier类，用来实现决策树分类

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split 
from sklearn.tree import DecisionTreeClassifier

X, y = load_iris(return_X_y=True)
# 为了后续的可视化方便，这里选择两个特征。
X = X[:, :2]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.25, random_state=0)
# criterion:不纯度度量标准，默认为gini。
# gini:基尼系数 entropy:信息熵
# splitter:选择分裂节点的方式。默认为best。
# best:在最好的位置分裂节点。 random:在随机的位置分裂节点。
# max_depth:树的最大深度，默认为None(不限制深度)。
# min_samples_split:分裂节点的最小样本数，默认为2。
# min_samples_leaf:分裂节点后，叶子节点最少的样本数量，默认为1。
# max_features:分裂节点时，考虑的最大特征数量，默认为None(考虑所有特征)。
# random_state:随机种子。
tree = DecisionTreeClassifier()
tree.fit(X_train, y_train)
print(tree.score(X_train, y_train))
print(tree.score(X_test, y_test))

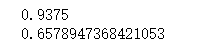
在这里插入图片描述
我们发现，模型存在严重的过拟合倾向，原因在于，如果没有指定树的深度，则默认会训练一棵完全生长的决策树（不限深度），这会导致模型复杂化，从而过分依赖于训练集数据的特性，造成过拟合。
我们可以从不同深度树的决策边界，来证实这一点。

from matplotlib.colors import ListedColormap
def plot_decision_boundary(model, X, y): 
    color = ["r", "g", "b"]
    marker = ["o", "v", "x"]
    class_label = np.unique(y)
    cmap = ListedColormap(color[: len(class_label)]) 
    x1_min, x2_min = np.min(X, axis=0)
    x1_max, x2_max = np.max(X, axis=0)
    x1 = np.arange(x1_min - 1, x1_max + 1, 0.02)
    x2 = np.arange(x2_min - 1, x2_max + 1, 0.02) 
    X1, X2 = np.meshgrid(x1, x2)
    Z = model.predict(np.c_[X1.ravel(), X2.ravel()]) 
    Z = Z.reshape(X1.shape)
    plt.contourf(X1, X2, Z, cmap=cmap, alpha=0.5) 
    for i, class_ in enumerate(class_label):
        plt.scatter(x=X[y == class_, 0], y=X[y == class_, 1], c=cmap.colors[i], label=class_, marker=marker[i])
    plt.legend()
plt.figure(figsize=(15, 10))
for index, depth in enumerate([1, 4, 7, 12], start=1):
    plt.subplot(2, 2, index)
    plt.title(f"最大深度:{depth}")
    tree = DecisionTreeClassifier(random_state=0, max_depth=depth) 
    tree.fit(X_train, y_train)
    plot_decision_boundary(tree, X_test, y_test)

在这里插入图片描述
对于决策树来说，最大深度对模型有着重要的影响，如果最大深度很小，意味着仅进行少数的分割，容易欠拟合，但是，如果最大深度很大，则意味着可能进行较多次切分，容易过拟合。

# 定义列表，用来存储在不同深度下，模型的分值。 
train_score = []
test_score = []
for depth in range(1, 13):
    tree = DecisionTreeClassifier(random_state=0, max_depth=depth) 
    tree.fit(X_train, y_train) 
    train_score.append(tree.score(X_train, y_train)) 
    test_score.append(tree.score(X_test, y_test))
plt.plot(train_score, marker="o", c="red", label="训练集") 
plt.plot(test_score, marker="o", c="green", label="测试集") 
plt.legend()

在这里插入图片描述
从运行结果中，我们可知，随着最大深度的增加，训练集的表现越来越好，但是测试集的表现，是先增后减。这说明在树深度较小是，模型是欠拟合的，因此，增加深度能够提升预测效果，但随着深度的增加，模型越来越依赖于训练集，这反而减低预测效果，造成过拟合。

Jahree

关注

0
点赞
踩
1

收藏

觉得还不错? 一键收藏
0
评论
机器学习--决策树

文章目录知识要点信息熵决策树原理决策树概念训练决策树预测原理分类决策树信息增益知识要点信息熵（1）概念信息熵，在1948年由香农提出。用来描述系统信息量的不确定度。不确定性越大，则信息熵越大，反之，信息熵越小。（2）计算方式假设随机变量X具有m个值，分别为：V1,V2,...,VmV_1,V_2,...,V_mV1,V2,...,Vm且P（X=V1）=p1P（X=V_1）= ...
复制链接

扫一扫