文章目录
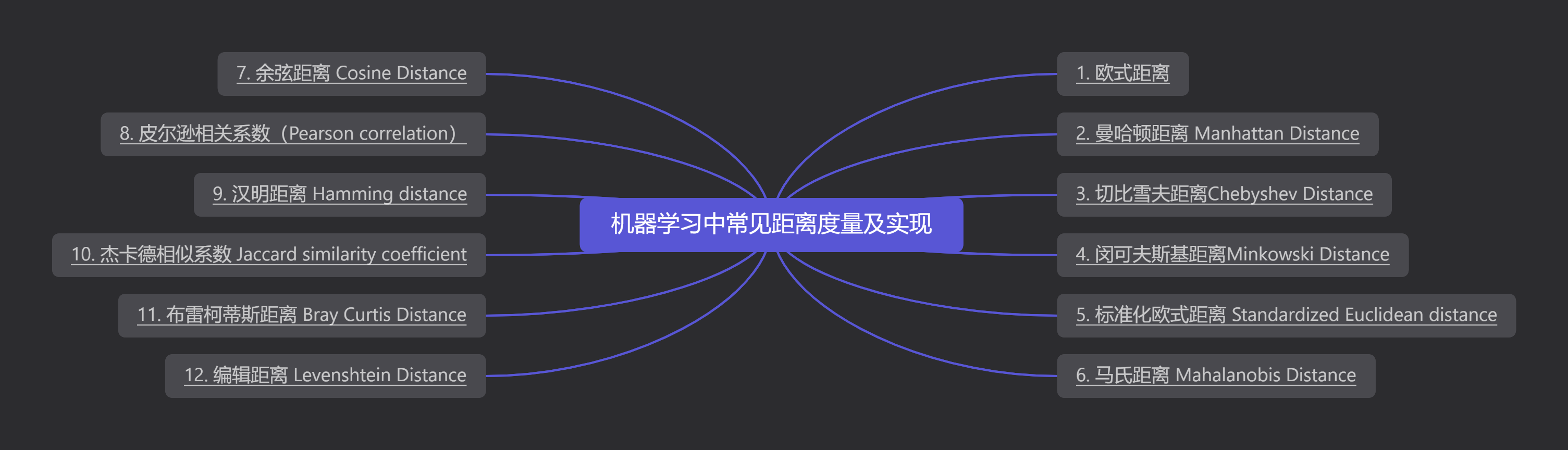
- 机器学习中常见距离度量及python实现
-
- 1. 欧式距离
- 2. 曼哈顿距离 Manhattan Distance
- 3. 切比雪夫距离Chebyshev Distance
- 4. 闵可夫斯基距离Minkowski Distance
- 5. 标准化欧式距离 Standardized Euclidean distance
- 6. 马氏距离 Mahalanobis Distance
- 7. 余弦距离 Cosine Distance
- 8. 皮尔逊相关系数(Pearson correlation)
- 9. 汉明距离 Hamming distance
- 10. 杰卡德相似系数 Jaccard similarity coefficient
- 11. 布雷柯蒂斯距离 Bray Curtis Distance
- 12. 编辑距离 Levenshtein Distance
机器学习中常见距离度量及python实现
1. 欧式距离
欧式距离是最易于理解的一种距离计算方法,源自欧式空间中两点间的距离公式。
- 二维平面上两点
a(x1, y1)与b(x2, y2)间的欧式距离
d 12 = ( x 1 − x 2 ) 2 + ( y 1 − y 2 ) 2 2 d_{12} =\sqrt [ 2 ]{ (x_1-x_2)^2+(y_1-y_2)^2 } d








 本文介绍了机器学习中常见的距离度量方法,包括欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、标准化欧式距离、马氏距离、余弦距离、皮尔逊相关系数、汉明距离、杰卡德相似系数、布雷柯蒂斯距离和编辑距离。每种距离度量都有其适用场景和优缺点,并提供了相应的Python实现。
本文介绍了机器学习中常见的距离度量方法,包括欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、标准化欧式距离、马氏距离、余弦距离、皮尔逊相关系数、汉明距离、杰卡德相似系数、布雷柯蒂斯距离和编辑距离。每种距离度量都有其适用场景和优缺点,并提供了相应的Python实现。

 订阅专栏 解锁全文
订阅专栏 解锁全文


















 1438
1438

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










