常用的距离度量方法

ILUUSION_S

已于 2025-02-25 15:38:48 修改

阅读量833

点赞数 7

分类专栏： LLM大模型学习文章标签： langchain

于 2025-02-25 15:38:13 首次发布

本文链接：https://blog.csdn.net/qq_42222846/article/details/145829907

版权

LLM大模型学习专栏收录该内容

16 篇文章

订阅专栏

常用的距离度量方法

距离度量方法主要用于计算给定问题空间中两个数据之间的差异，即数据集中的特征。然后可以使用该距离来确定特征之间的相似性，距离越小特征越相似。

在这里插入图片描述

以上分别是欧氏距离、曼哈顿举例、切比雪夫距离、闵可夫斯基距离、余弦距离、哈弗辛距离、汉明距离、杰卡德距离、索伦森-戴斯距离、动态时间规整。

距离度量的作用

通过合理选择和应用距离度量方法，可以提高数据分析和机器学习任务的效果和准确性：

数据聚类：距离度量在聚类算法（如K-means、层次聚类）中用于衡量数据点之间的相似性或差异性，帮助确定聚类的中心和边界。
分类问题：在K最近邻（K-NN）等分类算法中，距离度量用于计算待分类点与已知类别点的距离，以确定待分类点的类别。
降维：在多维标度法（MDS）和主成分分析（PCA）等降维技术中，距离度量用于保留数据点之间的相对距离，帮助在低维空间中重构高维数据。
异常检测：距离度量可用于检测数据中的异常点，通过计算数据点到中心或其他点的距离来判断其是否为异常值。
信息检索：在文本检索和推荐系统中，距离度量用于计算查询向量与文档向量之间的相似度，以返回最相关的文档或推荐内容
图像处理：在图像分类、分割等任务中，距离度量用于衡量图像特征向量之间的相似性，帮助识别和处理图像内容。

欧氏距离（Euclidean distance）

在这里插入图片描述

欧氏距离（Euclidean distance，也叫欧几里得距离或L2距离）以古希腊数学家欧几里得命名的距离度量方式，基于勾股定理计算，是最常见的距离度量方法之一，直观解释就是计算多维空间中两点的直线距离。计算公式如下所示：

在这里插入图片描述
上述公式表示计算在点x和点y在n维空间中的直线距离：

D(x,y)表示计算点x和点y之间的欧氏距离。
n表示空间的维度，即点x或点y的坐标数量。
(x_i-y_i)²表示点x和点y在第 i维空间上的坐标差值的平方
∑表示对所有维度上的坐标差进行求和。

代码实现如下：

"""原生实现"""
def original_euclidean_distance(x, y):
    distance = 0
    for i in range(len(x)):
        distance += (x[i] - y[i])**2
    return distance**0.5

x = [1,2,3]
y = [4,5,6]
print(original_euclidean_distance(x,y))


"""基于numpy"""
import numpy as np

def euclidean_distance(x, y):
    """欧氏距离"""
    return np.sqrt(np.sum((np.array(x) - np.array(y))**2))


x = [1,2,3]
y = [4,5,6]
print(euclidean_distance(x,y))


"""基于scipy"""
from scipy.spatial import distance
x = [1,2,3]
y = [4,5,6]
print(distance.euclidean(x, y))

优点：

几何直观：欧氏距离直观地表示了两点之间的直线距离，易于理解和可视化。
简单高效：计算简单，可以快速地在各种应用中实现。
广泛适用：适用于许多领域，如机器学习、计算机视觉、地理信息系统等。
数学性质良好：满足三角不等式，是真正意义上的度量（metric）。
与欧氏空间兼容：在欧氏空间中，欧氏距离是最短路径，这使得它在许多几何和物理问题中非常自然。

缺点：

对异常值敏感：由于欧氏距离是平方和的平方根，它对异常值（outliers）非常敏感。
不适用于高维空间：在高维空间中，欧氏距离可能会退化，导致所谓的“维度灾难”，距离的区分度降低。
尺度敏感：如果特征的尺度差异很大，欧氏距离可能会受到较大特征的影响，忽略较小特征的影响。
不适合非欧氏空间：在非欧氏空间（如球面或双曲空间）中，欧氏距离不适用。
计算成本：在大规模数据集上计算欧氏距离可能非常耗时，尤其是在需要频繁计算最近邻时。

适用场景：

低维空间：在二维或三维空间中，欧氏距离是一个很好的选择，因为它直观且计算简单。
特征尺度一致：当所有特征具有相似的尺度时，欧氏距离可以很好地工作。
聚类分析：在K-means等聚类算法中，欧氏距离是常用的距离度量。
最近邻搜索：在K-nearest neighbors（KNN）算法中，欧氏距离常用于找到最近的邻居点。
多维空间的降维：在PCA（主成分分析）等降维技术中，欧氏距离有助于识别数据的主要方向。
计算机视觉：在图像处理和计算机视觉中，欧氏距离可以用来衡量图像之间的相似性。

曼哈顿距离（Manhattan distance）

在这里插入图片描述

曼哈顿距离（Manhattan Distance，也叫城市街区距离、出租车距离、L1距离），来源于美国纽约市的曼哈顿区，表示两个点在标准坐标系上的绝对轴距总和，直观解释就是计算在标准坐标系中两点沿着坐标轴移动的距离。计算公式如下所示：

在这里插入图片描述

上述公式表示计算在点x和点y在k维空间中的直线距离：

D(x,y)表示计算点x和点y之间的曼哈顿距离。
k表示空间的维度，即x点或y点的坐标数量。
|x_i-y_i|表示点x和点y在第 i维空间上的坐标差值的绝对值。
∑表示对所有维度上的坐标差进行求和。

代码实现如下：

"""原生实现"""
def original_manhattan_distance(x, y):
    """曼哈顿距离"""
    distance = 0
    for i in range(len(x)):
        distance += abs(x[i] - y[i])
    return distance


x = [1,2,3]
y = [4,5,6]
print(original_manhattan_distance(x,y))

"""基于numpy"""
import numpy as np

def manhattan_distance(x, y):
    """曼哈顿距离"""
    return np.sum(np.abs(np.array(x) - np.array(y)))


x = [1,2,3]
y = [4,5,6]
print(manhattan_distance(x,y))


"""基于scipy"""
from scipy.spatial import distance

x = [1,2,3]
y = [4,5,6]

print(distance.cityblock(x, y))

优点

对尺度不敏感：曼哈顿距离对不同维度的尺度变化不敏感，即便各维度的单位不同，距离计算结果仍具有可靠性。
计算简单：曼哈顿距离的计算比欧氏距离简单，因为它只涉及绝对值和求和操作，无需进行平方和开平方操作。
适用于网格状路径：在城市规划、机器人路径规划等网格状布局的应用中，曼哈顿距离更加符合实际路径长度。

缺点

不考虑方向：曼哈顿距离只考虑各维度上的差值绝对值，忽略了数据点之间的方向信息，这在某些应用中可能导致信息丢失。
不适用于高维空间：在高维空间中，曼哈顿距离可能不如欧氏距离直观，并且随着维度增加，距离的分布可能变得更加稀疏。
对异常值敏感：曼哈顿距离对数据中的异常值（outliers）敏感，这些异常值会显著影响距离的计算结果。

适用场景：

路径规划：在城市交通规划和机器人路径规划中，曼哈顿距离可以用来估计从起点到终点的最短路径长度，特别是在只能沿着水平或垂直方向移动的情况下。
图像处理：在图像处理中，曼哈顿距离用于测量像素之间的差异，例如在图像分割和模式识别中。
机器学习：在机器学习中，曼哈顿距离常用于最近邻算法（k-NN）和聚类算法（如k-means）中，用以衡量样本之间的相似性。
数据挖掘：曼哈顿距离适用于数据挖掘和机器学习，如在k近邻(KNN)算法中计算样本之间的距离。

余弦距离（Cosine Distance）

在这里插入图片描述

余弦距离（Cosine Distance）是基于余弦相似度（Cosine Similarity）的一种距离度量方法，用于衡量两个向量之间的相似性。它通过计算两个向量之间的夹角余弦值，反映向量方向上的差异，而不考虑向量的大小。余弦距离经常被用作解决高维欧几里得距离问题，例如文本分析、信息检索等高维空间的应用场景。计算公式如下所示：

在这里插入图片描述

余弦相似度的取值范围是 ([-1, 1]），其中1表示向量完全同向，-1表示完全反向，0表示两向量正交（即相互独立）。上述公式表示计算在点x和点y在方向上的余弦距离：

D(x,y)：表示向量x和向量y之间的余弦距离或余弦相似度。
cos⁡(θ)：表示向量 x和向量y之间的夹角θ的余弦值。
x⋅y：表示向量x和向量x的点积（内积）。
||x||：表示向量x的范数（长度或模）。
||y||：表示向量 y的范数（长度或模）。

代码实现如下：

"""原生实现"""
def original_cosine_distance(x, y):
    """
    余弦距离
    余弦相似度 = 点积 / 模长
    """
    # 计算点积
    dot_product = sum(a * b for a, b in zip(x, y))

    # 计算向量x的模长
    norm_x = (sum(a ** 2 for a in x)) ** 0.5
    # 计算向量y的模长
    norm_y = (sum(b ** 2 for b in y)) ** 0.5
    # 计算余弦距离
    return 1 - dot_product / (norm_x * norm_y)


x = [1,2,3]
y = [4,5,6]
print(original_cosine_distance(x,y))


"""基于numpy"""
import numpy as np


def cosine_distance(x, y):
    """
    余弦距离
    余弦相似度 = 点积 / 模长
    """
    return 1 - np.dot(x, y) / (np.linalg.norm(np.array(x)) * np.linalg.norm(np.array(y)))

x = [1,2,3]
y = [4,5,6]
print(cosine_distance(x,y))


"""基于scipy"""
from scipy.spatial import distance
x = [1,2,3]
y = [4,5,6]
print(distance.cosine(x, y))

优点

尺度无关性：余弦距离只关注向量的方向，而不考虑向量的大小，因此它对特征值的尺度变化不敏感，特别适用于文本分析等场景。
直观性：余弦距离的值可以直观地解释为两个向量之间夹角的余弦值，这使得它在解释上较为直观。
适用于高维数据：在高维空间中，可以有效地捕捉向量之间的相似性，而不受维度灾难的影响，并且计算复杂度较低。

缺点

对零向量不定义：如果输入向量中存在零向量，则无法计算余弦相似度，进而无法计算余弦距离。
忽略向量大小：仅关注向量之间的角度，不能反映向量大小的差异，因此在某些应用中可能无法有效捕捉向量的实际差异。
适用场景有限：余弦距离在那些需要考虑向量大小的场景中表现不佳，例如图像分析、物理量度等领域。
大规模数据集中表现不佳：虽然余弦距离的计算相对简单，但在处理大规模数据时，计算所有向量对之间的余弦距离可能需要较高的计算资源。

应用场景：

文本分析：在自然语言处理中，余弦距离常用于比较文档或查询与文档之间的相似性。
推荐系统：在推荐系统中，余弦距离可以用来评估用户或物品之间的兴趣相似性。
聚类分析：在聚类算法中，如 K-means，余弦距离可以作为度量样本之间相似性的指标。
图像处理：在图像识别和分类任务中，余弦距离可以用来比较图像特征向量之间的相似性。

杰卡德距离(Jaccard Distance)

杰卡德距离（Jaccard Distance，也叫雅卡尔距离）是一种用于衡量两个集合之间相异性的度量方法。杰卡德距离是基于杰卡德相似系数（Jaccard Similarity Coefficient，也叫雅卡尔指数、IoU（交并比））来计算得到的。下面为杰卡德相似系数的图示：

在这里插入图片描述

杰卡德相似系数主要是通过计算2个集合的交集大小与并集大小之间的比率来衡量相似度，而杰卡德距离则与杰卡德相似系数互补。

杰卡德距离的计算公式如下所示：

在这里插入图片描述

杰卡德距离的取值范围从0到1，其中0表示两个集合完全相同，1表示两个集合完全不同。上述公式表示计算在集合x和集合y的杰卡德距离：

D(x,y)：表示集合x和集合y的杰卡德距离，杰卡德距离 = 1 - 杰卡德相似系数。
∣x∩y∣：表示集合x和集合y的交集大小，即两个集合中共有元素的数量。
∣x∪y∣：表示集合x和集合y的并集大小，即两个集合中所有独特元素的数量。

代码实现如下：

"""原生实现"""
def original_jaccard_distance(x, y):
    """
    杰卡德距离[广义jaccard仅用于计算实数数据]
    杰卡德距离 = 1 - 杰卡德相似系数
    """
    # 计算交集
    intersection = set(x).intersection(set(y))
    # 计算并集
    union = set(x).union(set(y))
    # 计算杰卡德相似系数
    jaccard_similarity = len(intersection) / len(union)

    # 计算杰卡德距离
    jaccard_distance = 1 - jaccard_similarity

    return jaccard_distance

x = [3, 4, 5, 6]
y = [3, 5, 4, 6]
print(original_jaccard_distance(x,y))


"""基于scipy"""
from scipy.spatial import distance
x = [0, 1, 0, 1]
y = [1, 1, 0, 1]
# scipy提供的jaccard算法，仅用于计算二元数据，属于狭义jaccard
print(distance.jaccard(x, y,))

优点：

简单直观，易于理解和计算。
尤其适用于衡量二元数据（如标签、集合）之间的差异，因为它只考虑元素的存在与否，通常用于使用二进制或二进制数据的应用程序，例如信息检索、文本分析、推荐系统等领域。

缺点：

忽略频次信息：杰卡德距离仅考虑集合中元素的存在与否，而忽略了元素在集合中出现的频次信息，因此在一些需要考虑频次的应用中不够精确。
不适用于有序数据：杰卡德距离不考虑数据的顺序信息，对于有序数据或连续数据的比较效果不佳。
对小集合敏感：对于元素较少的小集合，杰卡德距离可能过于敏感，即使两个集合只有一个元素不同，也可能导致较大的距离。

应用场景：

文本分析：用于比较文档或查询与文档之间的相似性，尤其是在处理词频向量时。
推荐系统：评估用户或物品之间的兴趣相似性。
数据去重：在数据清洗过程中识别重复记录。
图像处理：比较图像特征向量的相似性，用于图像检索或分类。
生物信息学：比较基因序列或蛋白质序列的相似性。

汉明距离（Hamming Distance）

在这里插入图片描述

汉明距离（Hamming Distance）是一种用于衡量两个等长字符串（或二进制数）之间差异的度量方法。它表示在两个字符串或二进制数对应位置上不同字符的数量，被广泛应用于编码理论、信息学、错误检测与纠正等领域。计算公式如下所示：

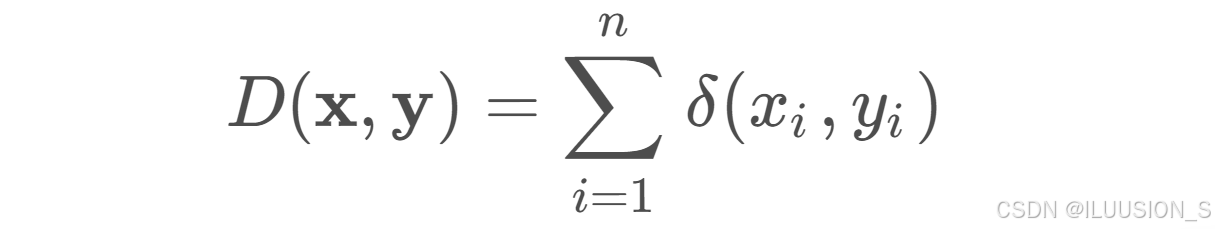
在这里插入图片描述

上述公式表示计算在等长的两个字符串x和y的汉明距离：

δ(x_i, y_i) 是一个指示函数，当x_i≠y_i时取值为 1，否则为 0。

代码实现如下：

"""原生实现"""
def original_hamming_distance(x, y):
    """
    汉明距离
    """
    if len(x) != len(y):
        raise ValueError("字符串长度必须相等")

    # 计算汉明距离
    return sum(xi != yi for xi, yi in zip(x, y))

x = "1011101"
y = "1001001"
print(original_hamming_distance(x,y))


"""基于scipy"""
from scipy.spatial import distance
x = "1011101"
y = "1001001"
# 使用scipy提供的hamming函数时，需要将字符串转换为列表或数组形式
print(distance.hamming(list(x), list(y),))