基于MATLAB的硬约束轨迹优化算法代码学习

本文是在学习路径规划算法中的一篇学习记录,将整个代码进行了详细的梳理,方便后来者参考学习.代码需要和理论部分结合起来看更容易理解,理论部分: 《软约束和硬约束下的轨迹优化-学习记录 》.

(代码注释中英夹杂,英文注释是原来作者的注释,中文注释是本人后来添加的)

0.结果展示

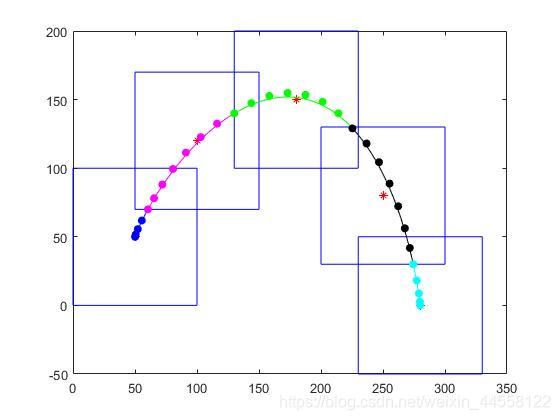
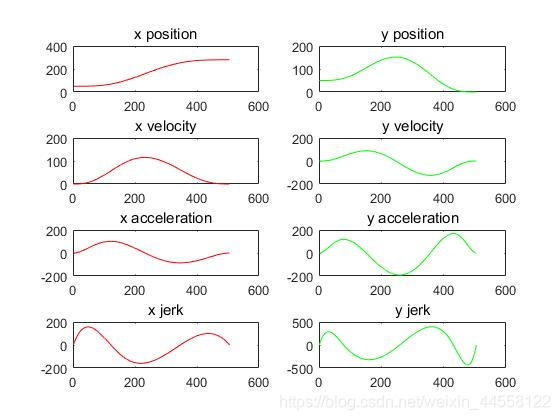
1.hw_6.m

         这部分是主函数部分，主要包括计算和画图。

clc;clear;close all
% 设定v、a、j的限制
v_max = 400;
a_max = 400;
j_max = 100000;
color = ['r', 'b', 'm', 'g', 'k', 'c', 'c'];

%% specify the center points of the flight corridor and the region of corridor
% 设定飞行走廊中心点
path = [50, 50;
       100, 120;
       180, 150;
       250, 80;
       280, 0];
% 设定飞行走廊x、y轴的边界
x_length = 100;
y_length = 100;

n_order = 7;   % 8 control points n_order = 2*d_order - 1 
% 7 = 2*4 -1 minimal snap defferenational order is 4, p,v,a,j must be
% continuous and differentialble, it can provide 2*4 euqtions, so the
% variables can be up to 8
n_seg = size(path, 1);

% 设定每个走廊的相关信息
corridor = zeros(4, n_seg);
for i = 1:n_seg
    % 对于每一列而言，前面两个是坐标，后面两个是走廊长宽
    corridor(:, i) = [path(i, 1), path(i, 2), x_length/2.0, y_length/2.0]';
end

%% specify ts for each segment
%每一段轨迹的时间分配为1s
ts = zeros(n_seg, 1);
for i = 1:n_seg
    ts(i,1) = 1;
end

% 独立对各轴求解
poly_coef_x = MinimumSnapCorridorBezierSolver(1, path(:, 1), corridor, ts, n_seg, n_order, v_max, a_max, j_max);
disp("x axle solved!")
poly_coef_y = MinimumSnapCorridorBezierSolver(2, path(:, 2), corridor, ts, n_seg, n_order, v_max, a_max, j_max);
disp("y axle solved!")
%% display the trajectory and cooridor
plot(path(:,1), path(:,2), '*r'); hold on;
for i = 1:n_seg
    plot_rect([corridor(1,i);corridor(2,i)], corridor(3, i), corridor(4,i));hold on;
end
hold on;

%% #####################################################
% STEP 4: draw bezier curve
x_pos = [];y_pos = [];
x_vel = [];y_vel = [];
x_acc = [];y_acc = [];
x_jerk = [];y_jerk = [];
idx = 1;
for j = 1:n_seg
    start_pos_id = idx;
    for t = 0:0.01:1
        x_pos(idx) = 0.0;y_pos(idx) = 0.0;
        x_vel(idx) = 0.0;y_vel(idx) = 0.0;
        x_acc(idx) = 0.0;y_acc(idx) = 0.0;
        x_jerk(idx) = 0.0;y_jerk(idx) = 0.0;
        for i = 0:n_order
            start_idx = (j-1)*(n_order+1)+i;
            basis_p = nchoosek(n_order, i) * t^i * (1-t)^(n_order-i);
            x_pos(idx) = x_pos(idx) + poly_coef_x(start_idx+1)*basis_p*ts(j);
            y_pos(idx) = y_pos(idx) + poly_coef_y(start_idx+1)*basis_p*ts(j);
            if i < n_order
                basis_v = nchoosek(n_order-1, i) * t^i *(1-t)^(n_order-1-i);
                x_vel(idx) = x_vel(idx) + (n_order+1) * (poly_coef_x(start_idx+2)-poly_coef_x(start_idx+1))*basis_v;
                y_vel(idx) = y_vel(idx) + (n_order+1) * (poly_coef_y(start_idx+2)-poly_coef_y(start_idx+1))*basis_v;
            end
            if i < n_order-1
                basis_a = nchoosek(n_order-2, i) * t^i *(1-t)^(n_order-2-i);
                x_acc(idx) = x_acc(idx) + (n_order+1) * n_order * (poly_coef_x(start_idx+3) - 2*poly_coef_x(start_idx+2) + poly_coef_x(start_idx+1))*basis_a/ts(j);
                y_acc(idx) = y_acc(idx) + (n_order+1) * n_order * (poly_coef_y(start_idx+3) - 2*poly_coef_y(start_idx+2) + poly_coef_y(start_idx+1))*basis_a/ts(j);
            end
            if i < n_order-2
                basis_j = nchoosek(n_order-3, i) * t^i *(1-t)^(n_order-3-i);
                x_jerk(idx) = x_jerk(idx) + (n_order+1) * n_order * (n_order-1) * ...
                    (poly_coef_x(start_idx+4) - 3*poly_coef_x(start_idx+3) + 3*poly_coef_x(start_idx+2) - poly_coef_x(start_idx+1)) * basis_j/ts(j)^2;
                y_jerk(idx) = y_jerk(idx) + (n_order+1) * n_order * (n_order-1) * ...
                    (poly_coef_y(start_idx+4) - 3*poly_coef_y(start_idx+3) + 3*poly_coef_y(start_idx+2) - poly_coef_y(start_idx+1)) * basis_j/ts(j)^2;
            end
        end
        idx = idx + 1;
    end
    end_pos_id = idx - 1;
    scatter(ts(j)*poly_coef_x((j-1)*(n_order+1)+1:(j-1)*(n_order+1)+1+n_order), ts(j)*poly_coef_y((j-1)*(n_order+1)+1:(j-1)*(n_order+1)+1+n_order), 'filled',color(mod(j,7)+1),'LineWidth', 5);hold on;
    plot(x_pos(start_pos_id:end_pos_id), y_pos(start_pos_id:end_pos_id), color(mod(j,7)+1));hold on;
end

figure(2)
subplot(4,2,1)
plot(x_pos, 'Color', 'r');title('x position');
subplot(4,2,2)
plot(y_pos, 'Color', 'g');title('y position');
subplot(4,2,3)
plot(x_vel, 'Color', 'r');title('x velocity');
subplot(4,2,4)
plot(y_vel, 'Color', 'g');title('y velocity');
subplot(4,2,5)
plot(x_acc, 'Color', 'r');title('x acceleration');
subplot(4,2,6)
plot(y_acc, 'Color', 'g');title('y acceleration');
subplot(4,2,7)
plot(x_jerk, 'Color', 'r');title('x jerk');
subplot(4,2,8)
plot(y_jerk, 'Color', 'g');title('y jerk');


function poly_coef = MinimumSnapCorridorBezierSolver(axis, waypoints, corridor, ts, n_seg, n_order, v_max, a_max, j_max)
    start_cond = [waypoints(1), 0, 0, 0];
    end_cond   = [waypoints(end), 0, 0, 0];   
    
    %% #####################################################
    % STEP 1: compute Q_0 of c'Q_0c
    [Q, M]  = getQM(n_seg, n_order, ts);
    Q_0 = M'*Q*M;
    % 返回和Q矩阵距离最近的一个对称正定(Symmetric Positive Definite)矩阵Q'.
    % 目的是在把目标函数微调为一个凸函数,保证得到的解为全局最优解.
    Q_0 = nearestSPD(Q_0);
    
    %% #####################################################
    % STEP 2: get Aeq and beq
    [Aeq, beq] = getAbeq(n_seg, n_order, ts, start_cond, end_cond);
    
    %% #####################################################
    % STEP 3: get corridor_range, Aieq and bieq
    
    % STEP 3.1: get corridor_range of x-axis or y-axis,
    % you can define corridor_range as [p1_min, p1_max;
    %                                   p2_min, p2_max;
    %                                   ...,
    %                                   pn_min, pn_max ];
    corridor_range = zeros(n_seg,2);
    for k = 1:n_seg
        % 横坐标/纵坐标减去、加上corridor宽度得到x/y轴边界
        corridor_range(k,:) = [corridor(axis,k) - corridor(axis+2,k), corridor(axis,k) + corridor(axis+2,k)];
    end
    
    % STEP 3.2: get Aieq and bieq
    [Aieq, bieq] = getAbieq(n_seg, n_order, corridor_range, ts, v_max, a_max, j_max);
    
    f = zeros(size(Q_0,1),1);
    % quadprog函数参数介绍：https://blog.csdn.net/tianzy16/article/details/87916128
    poly_coef = quadprog(Q_0,f,Aieq, bieq, Aeq, beq);
end

function plot_rect(center, x_r, y_r)
    p1 = center+[-x_r;-y_r];
    p2 = center+[-x_r;y_r];
    p3 = center+[x_r;y_r];
    p4 = center+[x_r;-y_r];
    plot_line(p1,p2);
    plot_line(p2,p3);
    plot_line(p3,p4);
    plot_line(p4,p1);
end

function plot_line(p1,p2)
    a = [p1(:),p2(:)];    
    plot(a(1,:),a(2,:),'b');
end

2.getQM.m

         获得Q矩阵。

function [Q, M] = getQM(n_seg, n_order, ts)
    Q = [];
    M = [];
    % 因为我们将时间映射到[0,1]区间内，所以这个getM函数可以固化下来
    M_k = getM(n_order);
    % d_order = 4;
    for k = 1:n_seg
        %#####################################################
        % STEP 2.1 calculate Q_k of the k-th segment 
        % Q_k = [];
        fac = @(x) x*(x-1)*(x-2)*(x-3);
        Q_k = zeros(n_order+1,n_order+1);

        for i = 0:n_order
            for j = 0:n_order
                if (i < 4) || (j < 4)
                    continue;
                else
                    % 也即 i!/(i-4)! * j!/(j-4)! * 1/(i+j-7) * t^(j+i-7)
                    Q_k(i+1,j+1) = fac(i) * fac(j)/(i + j - 7) * ts(k)^(j+i-7); 
                end
            end
        end
        Q = blkdiag(Q, Q_k);
        M = blkdiag(M, M_k);
    end
end

3.getM.m

         获得M矩阵。

function M = getM(n_order)
    if n_order == 3
        M = [ 1   0   0  0;
              -3   3   0  0;
               3  -6   3  0;
              -1   3  -3  1];
    elseif n_order == 4       % Degree D = 4
        M = [1   0   0   0  0 ;
             -4   4   0   0  0 ;
              6 -12   6   0  0 ;
             -4  12 -12   4  0 ;
              1  -4   6  -4  1 ];
    elseif n_order == 5  % Degree D = 5
        M = [1   0   0   0  0  0
             -5   5   0   0  0  0;
             10 -20  10   0  0  0;
            -10  30 -30  10  0  0;
             5  -20  30 -20  5  0;
            -1    5 -10  10 -5  1 ];    
    elseif n_order == 6  % Degree D = 6
        M = [1    0    0    0    0    0    0;
             -6    6    0    0    0    0    0;
             15  -30   15    0    0    0    0; 
            -20   60  -60   20    0    0    0;
             15  -60   90  -60   15    0    0;
             -6   30  -60   60  -30    6    0;
              1   -6   15  -20   15   -6    1 ];
    elseif n_order == 7 % Degree D = 7
        M = [ 1    0    0    0    0   0  0  0;
              -7    7    0    0    0   0  0  0;
              21  -42   21    0    0   0  0  0
             -35  105 -105   35    0   0  0  0;
              35 -140  210 -140   35   0  0  0;
             -21  105 -210  210 -105  21  0  0;
               7  -42  105 -140  105 -42  7  0;
              -1   7   -21   35  -35  21 -7  1];
    elseif n_order == 8 % Degree D = 8
        M = [ 1    0    0    0    0    0   0  0  0 ;
              -8    8    0    0    0    0   0  0  0;
              28  -56   28    0    0    0   0  0  0;
             -56  168 -168   56    0    0   0  0  0;
              70 -280  420 -280   70    0   0  0  0;
             -56  280 -560  560 -280   56   0  0  0;
              28 -168  420 -560  420 -168  28  0  0;
              -8   56 -168  280 -280  168 -56  8  0;
               1   -8   28  -56   70  -56  28 -8  1];
    elseif n_order == 9 % Degree D = 9
        M = [ 1    0    0      0     0     0    0    0   0 0;
              -9    9    0      0     0     0    0    0   0 0;
              36  -72   36      0     0     0    0    0   0 0;
             -84  252 -252     84     0     0    0    0   0 0;
             126 -504  756   -504    126    0    0    0   0 0;
            -126  630 -1260  1260   -630   126   0    0   0 0;
              84 -504  1260 -1680   1260  -504   84   0   0 0;
             -36  252 -756   1260  -1260   756  -252  36  0 0;
               9  -72  252   -504    630  -504   252 -72  9 0;
              -1    9  -36     84   -126   126  -84   36 -9 1];
    end
end

4.getAbeq.m

         获得线性等式约束的系数矩阵和右端向量。

function [Aeq, beq] = getAbeq(n_seg, n_order, ts, start_cond, end_cond)
    n_all_poly = n_seg*(n_order+1); % 所有控制点多项式系数总和
    %#####################################################
    % STEP 2.1 p,v,a,j constraint in start 
    Aeq_start = zeros(4, n_all_poly); % Ascending order
    Aeq_start(1,1:4) = [1,0,0,0] * ts(1)^(1);% c0
    Aeq_start(2,1:4) = n_order * [-1,1,0,0] * ts(1)^(0);% c'0 = n*(c1 - c0)
    Aeq_start(3,1:4) = n_order * (n_order-1) * [1,-2,1,0] * ts(1)^(-1);% c''0 = n*(n-1)*(c2 -2*c1 +c0)   
    Aeq_start(4,1:4) = n_order * (n_order-1) * (n_order-2) * [1,-3,3,-1] * ts(1)^(-2);% c''0 = n*(n-1)*(n-2)*(c3 - 3*c2 + 3*c1 - c0)   

    beq_start =  start_cond';
    
    %#####################################################
    % STEP 2.2 p,v,a,j constraint in end
    Aeq_end = zeros(4, n_all_poly); % Descending order
    Aeq_end(1,end-3:end) = [1,0,0,0] * ts(end)^(1);% cn
    Aeq_end(2,end-3:end) = n_order * [-1,1,0,0] * ts(end)^(0);% c'n-1 = n*(cn -cn-1)
    Aeq_end(3,end-3:end) = n_order * (n_order-1) * [1,-2,1,0]  * ts(end)^(-1);% c''n-2 = n^2*(n-1)*(cn - 2*cn-1 + cn-2)    
    Aeq_end(4,end-3:end) = n_order * (n_order-1) * (n_order-2) * [1,-3,3,-1] * ts(end)^(-2);% c''n-3 = n*(n-1)*(n-2)*(cn - 3*cn-1 + 3*cn-2 - c0)   

    beq_end = end_cond';
    
    %#####################################################
    % STEP 2.3 position continuity constrain between 2 segments
    Aeq_con_p = zeros(n_seg-1, n_all_poly); % n_seg-1:轨迹段数
    d = 0; % 导数阶数
    for k = 1:n_seg-1
        Aeq_con_p(k,k*(n_order+1)) = 1 * ts(k)^(1-d);
        Aeq_con_p(k,k*(n_order+1)+1) = -1 * ts(k+1)^(1-d);
    end
    
    beq_con_p = zeros(n_seg-1,1);

    %#####################################################
    % STEP 2.4 velocity continuity constrain between 2 segments
    Aeq_con_v =  zeros(n_seg-1, n_all_poly);
    d = 1;
    for k = 1:n_seg-1 % (c(n))- c(n-1)) segment 1 + (-c1 + c0) segment 2
        Aeq_con_v(k,k*(n_order+1)-1:k*(n_order+1)) = [-1, 1] * ts(k)^(1-d);
        Aeq_con_v(k,k*(n_order+1)+1:k*(n_order+1)+2) = [1, -1] * ts(k+1)^(1-d);
    end    
    beq_con_v = zeros(n_seg-1,1);

    %#####################################################
    % STEP 2.5 acceleration continuity constrain between 2 segments
    Aeq_con_a = zeros(n_seg-1, n_all_poly);
    d = 2;
    for k = 1:n_seg-1 % (c(n))- 2*c(n-1) + c(n-2)) segment 1 + (-c2 + 2*c1 - c0) segment 2
        Aeq_con_a(k,k*(n_order+1)-2:k*(n_order+1)) = [1, -2, 1] * ts(k)^(1-d);
        Aeq_con_a(k,k*(n_order+1)+1:k*(n_order+1)+3) = [-1, 2, -1] * ts(k+1)^(1-d);
    end  
    beq_con_a = zeros(n_seg-1,1);

    %#####################################################
    % STEP 2.6 jerk continuity constrain between 2 segments
    Aeq_con_j = zeros(n_seg-1, n_all_poly);
    d = 3;
    for k = 1:n_seg-1 % (c(n))- 3*c(n-1) + 3*c(n-2) - c(n-3)) segment 1 + (-c3 + 3*c2 - 3*c1 + c0) segment 2
        Aeq_con_j(k,k*(n_order+1)-3:k*(n_order+1)) = [1, -3, 3, -1] * ts(k)^(1-d);
        Aeq_con_j(k,k*(n_order+1)+1:k*(n_order+1)+4) = [-1, 3, -3, 1] * ts(k+1)^(1-d);
    end  
    beq_con_j = zeros(n_seg-1,1);
    %#####################################################
    % combine all components to form Aeq and beq   
    Aeq_con = [Aeq_con_p; Aeq_con_v; Aeq_con_a; Aeq_con_j];
    beq_con = [beq_con_p; beq_con_v; beq_con_a; beq_con_j];
    Aeq = [Aeq_start; Aeq_end; Aeq_con];
    beq = [beq_start; beq_end; beq_con];
end

5.getAbieq.m

         获得线性不等式约束的系数矩阵和右端向量。

function [Aieq, bieq] = getAbieq(n_seg, n_order, corridor_range, ts, v_max, a_max, j_max)
    n_all_poly = n_seg*(n_order+1);
    %#####################################################
    % STEP 3.2.1 p constraint
    % 安全性约束
    coeff_p = ones(n_all_poly,1);
    bieq_p = [];
    for k = 1:n_seg % max
        % 这个没有完全理解为什么要这么构造？
        coeff_p(1 + (k-1)*(n_order+1):k*(n_order+1)) = coeff_p(1 + (k-1)*(n_order+1):k*(n_order+1)) * ts(k)^(1);
        % 放入上边界
        bieq_p = [bieq_p;ones(n_order+1,1)*corridor_range(k,2)];
    end
    for k = 1:n_seg % -min
        % 放入下边界
        bieq_p = [bieq_p;ones(n_order+1,1)*corridor_range(k,1)*(-1)];
    end
    Aieq_p = diag(coeff_p,0);
    Aieq_p = [Aieq_p;-Aieq_p];

    %#####################################################
    % STEP 3.2.2 v constraint  
    % 动力学约束: v
    n_ctr = n_order;      % the number of control posints after first deferention: n_order 
    n_eq = n_ctr*n_seg*2; % number of equations (max and min constraints)
    Aieq_v = zeros(n_eq/2,n_all_poly);

    for k = 1:n_seg
        for n = 1:n_ctr
            index_col = k*(n_order+1)-1;
            index_row = n+(k-1)*n_ctr;
            Aieq_v(index_row,index_col:index_col+1) = n_order * [-1, 1] * ts(k)^(0);
        end
    end
    Aieq_v = [Aieq_v;-Aieq_v];
    bieq_v = ones(n_eq,1)* v_max;
  
%     bieq_v = ones(n_eq/2,1)* v_max;

    %#####################################################
    % STEP 3.2.3 a constraint 
    % 动力学约束: a
    n_ctr = n_order-1;    % the number of control posints after second deferention: n_order - 1 
    n_eq = n_ctr*n_seg*2; % number of equations (max and min constraints)
    Aieq_a = zeros(n_eq/2, n_all_poly);
    
    for k = 1:n_seg
        for n = 1:n_ctr
            index_col = k*(n_order+1)-2;
            index_row = n+(k-1)*n_ctr;
            Aieq_a(index_row,index_col:index_col+2) = n_order * (n_order-1) * [1, -2, 1] * ts(k)^(-1);
        end
    end
    Aieq_a = [Aieq_a;-Aieq_a];
    bieq_a = ones(n_eq,1)*a_max;

%     bieq_a = ones(n_eq/2,1)*a_max;

    % STEP 3.2.4 j constraint 
    n_ctr = n_order-2;    % the number of control posints after third deferention: n_order - 2
    n_eq = n_ctr*n_seg*2; % number of equations (max and min constraints)
    Aieq_j = zeros(n_eq/2, n_all_poly);
    
    for k = 1:n_seg
        for n = 1:n_ctr
            index_col = k*(n_order+1)-3;
            index_row = n+(k-1)*n_ctr;
            Aieq_j(index_row,index_col:index_col+3) = n_order * (n_order-1) * (n_order-2) * [1, -3, 3, -1] * ts(k)^(-2);
        end
    end
    Aieq_j = [Aieq_j;-Aieq_j];
    bieq_j = ones(n_eq,1)*j_max;


    %#####################################################
     % combine all components to form Aieq and bieq  

    Aieq = [Aieq_p; Aieq_v; Aieq_a; Aieq_j];
    bieq = [bieq_p; bieq_v; bieq_a; bieq_j];
%     Aieq = Aieq_p;
%     bieq = bieq_p;
end

6.参考引用

         1.理论:深蓝学院<<移动机器人运动规划>>;
         2.代码:https://github.com/KailinTong/Motion-Planning-for-Mobile-Robots/tree/master/hw_6