【数学基础】矩阵的特征向量、特征值及其含义
在线代课上,老师会教我们怎么求矩阵的特征值与特征向量。但是并不会讲特征值与特征向量到底有着什么样的几何意义或者物理意义,或许讲了但也比较模糊。矩阵的特征值与特征向量在各种机器学习算法与应用场景中都有出现,每次出现都有着其独特的意义。在这里也只是简述一二。
一、方阵的特征值与特征向量
1、特征值与特征向量的定义:
定义1:设是
阶方阵,若数
和
维非零列向量
,使得
成立,则称
是方阵
的一个特征值,
为方阵
的对应于特征值
的一个特征向量。
注:
是方阵。(对于非方阵,是没有特征值的,但会有条件数。)
- 特征向量
为非零列向量。
2、特征值与特征向量的几何意义(引自https://www.matongxue.com/madocs/228.html):
我们先记线性变换一个T(Transformation)为,容易知道矩阵
代表一个线性变换,可以做升维降维,放大缩小以及旋转的线性变换,而对于方阵
而言,是不存在升维降维的。即一个方阵
其对向量
的线性变换为伸长收缩或者旋转。
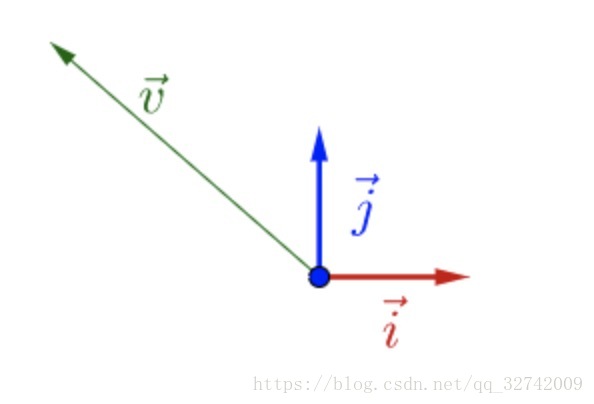
在为基向量的空间下有个向量
:
对随便左乘一个矩阵
,即对
进行一个线性变换。
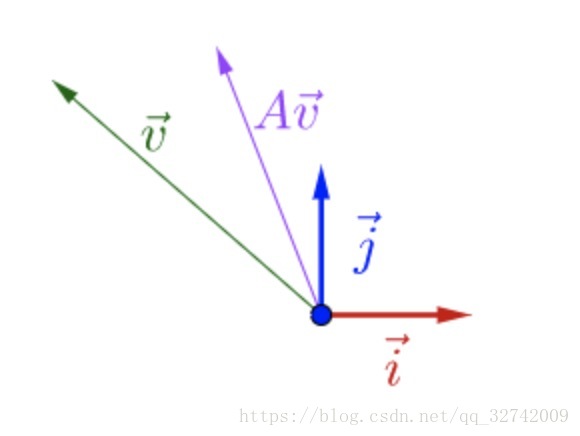
调整下的方向,使其特殊一点。
可以观察到,调整后的和
在同一直线上,只是
的长度相对
的长度变长了。
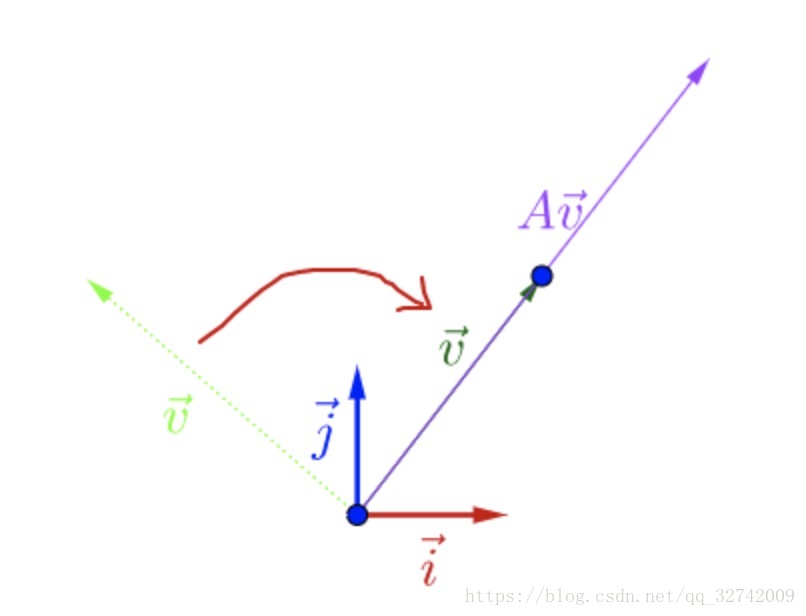
此时,我们就称是
的特征向量,而
的长度是
的长度的
倍,
就是特征值。
即
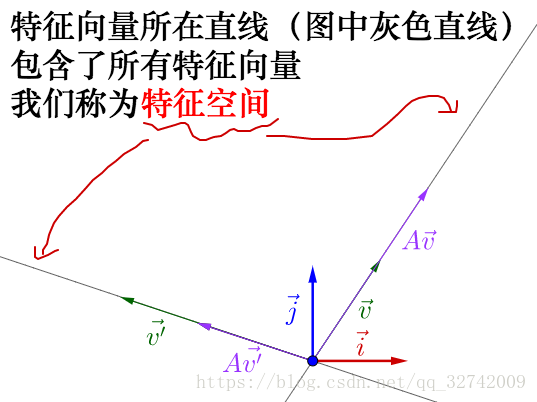
从特征向量和特征值的定义中还可以看出,特征向量所在直线上的向量都是特征向量。
3、特征值与特征向量的一些性质
1)、如果是一个不可逆方阵,即
,则齐次线性方程组
有无穷多解,故有非零解,即
,故不可逆方阵必有零特征值
。
2)、一些实际问题中,常常会涉及到一系列的运算,,由特征值和特征向量的关系
可以简化这些运算,
。
3)、矩阵的迹trace,即为矩阵的对角元素之和。例记
,则
。
的特征值为
;
的特征值为
;
的特征值为
,侧面也说明了非满秩矩阵不可逆。
- 若
,则
是
对应的特征值。
- 在复数域中,任意的方阵
都存在对应的特征值与特征向量。在实数域中则不一定。
4)、特征向量的性质
- 矩阵
关于特征值
的
个特征向量
的任意非零线性组合
还是
的关于
的特征向量。
- 设
是矩阵
的不同特征值所对应的特征向量,则
是线性无关的。
阶方阵
至多有
个线性无关的特征向量。
- 矩阵
与
的特征值相同,但特征向量却未必一样。
- 设
为
阶方阵
的一个
重特征值,
关于
的线性无关的特征向量的最大个数为
,则
。
二、特征值与特征向量的计算
- 求出方阵
的特征多项式
。
- 解特征方程
,求出
的全部特征值
。其中
的
重根对应
的
个值相同的特征值。
- 求
或
的非零解,得到
的关于
的全部特征向量。
例1:求矩阵的特征值和全部特征向量。
第一步:写出矩阵的特征方程,求出特征值。
特征值为
三阶方阵的行列式计算:
第二步:对每个特征值代入齐次线性方程组
,求非零解。
当时,齐次线性方程组为
系数矩阵
自由未知量:
令
得基础解系:
所以是对应于
的全部特征向量。
当时,齐次线性方程组为
系数矩阵
,得基础解系
所以是对应于
的全部特征向量。
三、特征值与特征向量的含义
上面一二两大点旨在回忆特征值与特征向量的定义与计算,对于为什么这样定义并未做过多的讲解。接下来进入重点,讲一下特征值与特征向量到底发挥了怎样的作用,以及为什么会将这样的向量定义为矩阵的特征向量。
乘幂法求矩阵的特征值及特征向量
上面求解矩阵特征值与特征向量的方法是常规的方法,不过在非常大时,直接求解特征值及其对应的特征向量开销会很大,因此可以用乘幂法解其数值。
假定阶矩阵
对应的
个特征值按模从大到小的排序为:
关于的特征向量
线性无关,此时特征向量
可以作为空间的一组基。
任取初始向量,建立迭代公式:
.
……………………
因为,故当
,
。因此
可看成是关于特征值
的近似特征向量,不过有个缺点就是当
(或
),
中不为0的分量将随k的增大而无限增大,计算机就有可能出现上溢(或下溢)。所以在实际计算时,需按规范法计算,每步先对向量
进行规范化:
通过上面的分析,可将乘幂法求矩阵的特征值及特征向量的方法可归纳如下:
-
计算特征值
,任选一个向量
,递归
;
-
当
充分大时或误差 Frobenius Norm
足够小时,停止;
-
就是当前
的主特征向量,对应的特征值为:
<p>λi=maxxk(xk中的最大分量);</p> <p> </p> </li> <li> <p>在A中去掉主特征λi对应向量的因素 </p> <p>A=A−λizkzTk,</p> 接下来再找下一个特征对,然后类似计算。 <p> </p> </li>
针对特征值相等的情况,假定|λ1|=|λ2|=…=|λm|>|λm+1|>…>|λn|,由于向量α1v1+α2v2+α3v3+…+αmvm仍是属于λ1的特征向量,故利用上述方法依旧可求解λ1,λm+1,…,λi特征值及其对应的特征向量。
运动
1、从调色谈起
我有一管不知道颜色的颜料,而且这管颜料有点特殊,我不能直接挤出来看颜色,只能通过调色来观察:
为了分辨出它是什么颜色(记得它只能通过调色来辨别):
因为反复混合之后,这管颜料的特征就凸显了出来,所以我们判断,这管颜料应该是蓝色。
说这个干什么?矩阵也有类似的情况。
2、矩阵的混合
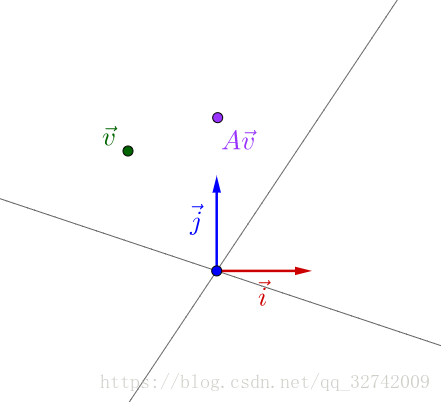
一般来说,矩阵我们可以看作某种运动,而二维向量可以看作平面上的一个点(或者说一个箭头)。对于点我们是可以观察的,但是运动我们是不能直接观察的。
就好像,跑步这个动作,我们不附加到具体的某个事物上是观察不到的,我们只能观察到:人跑步、猪跑步、老虎跑步、......,然后从中总结出跑步的特点。
就好像之前举的不能直接观察的颜料一样,要观察矩阵所代表的运动,需要把它附加到向量上才观察的出来:
似乎还看不出什么。但是如果我反复运用矩阵乘法的话:
至于为什么会产生这样的现象,可以通过乘幂法来证明。
就像之前颜料混合一样,反复运用矩阵乘法,矩阵所代表的运动的最明显的特征,即速度最大的方向,就由最大特征值对应的特征向量展现了出来。利用乘幂法的思想,每次将最大的特征值对应的向量因素从矩阵中除去,就可以依次得到各个特征值所对应的特征向量。
OK!知道了上述运动这个关系之后,我们可以思考这样一件事情。
1、解释1
我们可以将矩阵看成是一个力的混合体,但需要注意的是,这个力的混合体中各个力是相互独立的!即特征向量之间线性无关,是无法做力的合成(这里只是假设其无法合成,有更好的解释以后会补充)的。其中力的个数为矩阵
的秩,力的大小为特征值的大小,力的方向即为特征向量的方向。
此时如果我们对任一向量(这里可以把
看成是一个物体,如一个小方块)无限施加这个力的集合,正如上图所示的那样,最终小方块运动的方向即为力最大的那个方向。即向量
会收敛为最大特征值
的特征向量。去掉这个力,不断重复,即可以得到第二个、第三个特征向量。
这就是为什么我们将这样的向量定义为矩阵的特征向量,因为一方面它能够体现出线性变换
中力的方向及大小,另一方面可以可以通过分析特征值得到该线性变换的主导因素。
再啰嗦几句,概括来说就是,特征值与特征向量可以告诉我们这个矩阵它产生的线性变换做了什么以及主要做了什么。
2、解释2
另一个更直观的解释就是颜料混合。我们将矩阵看成一个篮子,重点不在篮子。在篮子里面有一堆颜料,包含了
种颜色,
为矩阵
的秩,但每种颜色的分量都不一样。先上结论——特征值代表了分量,特征向量表示了颜色。对任一向量
(这里可以把
看成是一滩液体,无所谓本来是什么颜色),每次施加矩阵
变换就是把篮子里的所有颜料都泼进去,泼无数次,最后清水的颜色就变成了颜色最多的颜色(这里不要计较什么颜料无限混合最后都是黑色灰色的,直观一点理解)。
假设我们现在有办法可以去掉篮子中指定颜色的所有颜料。则可以依次根据特征值排序得到特征向量。
通过这么一个比喻,我们也可以得出同样的结论。
矩阵包含了一堆信息——颜料的种类与颜料的数量。如果我们可以通过矩阵分解将其分离出来,保留那些分量大的颜色,而去除那些可有可无的颜色就可以实现信息压缩等变换。
OK!到此大致讲解了三块内容:1、特征值与特征向量的定义及性质。2、特征值与特征向量的计算。3、特征值与特征向量的直观解释与含义。
线性代数中还有很多的概念,想要彻底搞清楚特征值与特征向量在实际应用中发挥的作用,需要连贯各种知识点。接下来会写一系列的文章来加深那些即将被遗忘的知识……








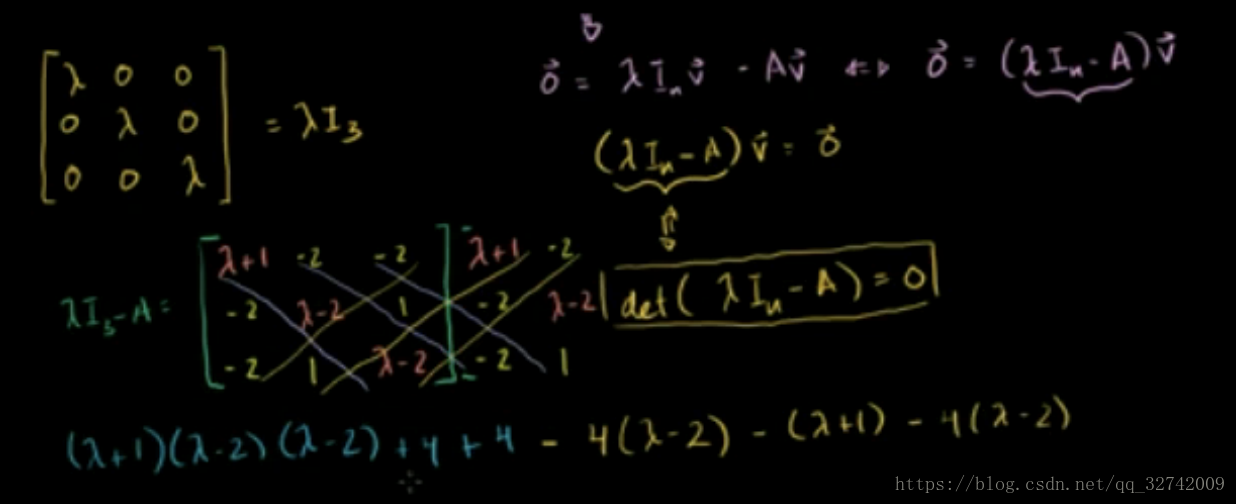
















 9万+
9万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








