【数字电子技术 Digital Electronic Technology 9】—— 脉冲波形的产生和整形电路（2）555定时器以及它的应用

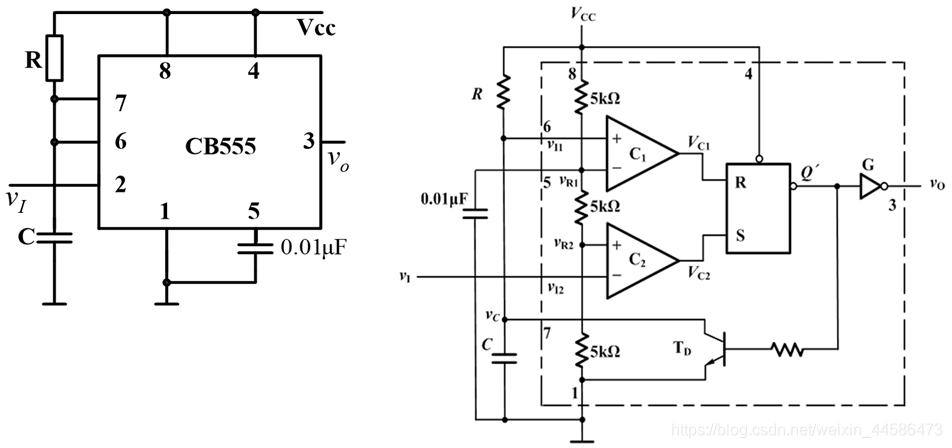
1.555定时器的原理剖析：

我们先来看看555定时器的内部电路图：

其中我们要说明的是：上图中的$C_1,C_2$是比较器，就是它会比较同相输入端“+”和反相输入端”-“的电压，如果“+”输入端的电压高于“-”输入端的电压，那么比较器输出高电平；反之，如果“-”端的电压高于“+"端的电压，那么输出低电平。

从上图，我们可以知道，比较器$C_1$两端的输入电压分别为：$v_{I1}$，$v_{R1}$；$C_2$两端的输入电压分别为：$v_{R2}$和$v_{I2}$。

当$V_{CO}$不接外电源的时候，$v_{R1},v_{R2}$就是电阻的分压，因此$v_{R1}=\frac{2}{3}{V}_{CC}$，$v_{R2}=\frac{1}{3}{V}_{CC}$.
注意：如果$V_{CO}$接了外部电源$v_0$，那么$v_{R1}=v_0$，$v_{R2}=\frac{1}{2}{v}_0$
下面我们就分别来讨论当$v_{I1},v_{I2}$取到不同的值的时候的输出情况：

$v_{I1}$	$v_{I2}$	$V_{C1}$( R )	$V_{C2}$( S )	$v_o$
>$\frac{2}{3}{V}_{CC}$	$>\frac{1}{3}{V}_{CC}$	1	0	0
>$\frac{2}{3}{V}_{CC}$	$<\frac{1}{3}{V}_{CC}$	1	1	1
<$\frac{2}{3}{V}_{CC}$	$>\frac{1}{3}{V}_{CC}$	0	0	不变
<$\frac{2}{3}{V}_{CC}$	$<\frac{1}{3}{V}_{CC}$	0	1	1

下面给出555定时器的逻辑图形符号和特性表：

【端口说明】：5端口是一个电压控制信号，如果这个5端口没有外接电源的话，那么那两个比较器的基准参考电压就是$\frac{2}{3}{V}_{CC}$和$\frac{1}{3}{V}_{CC}$，如果5端口接了外电源$v$，那么两个比较器$C_1,C_2$的基准参考电压就是$v$和$\frac{1}{2}v$

2.用555定时器接成施密特触发电路：

【应试技巧：555定时器如果把2，6连在一起共同作为输入端的话，就是施密特触发电路】
既然是连结成了施密特触发电路，那么无非就是要你求几个参数：$V_T^{+},V_T^{-}$和$△V_T$
这并不难，还是一样的：如果$V_{CO}$也就是5脚没有接外电源，那么则$V_T^{+}=\frac{2}{3}{V}_{CC}$；$V_T^{-}=\frac{1}{3}{V}_{CC}$,$△V_T=\frac{1}{3}{V}_{CC}$；如果5脚接了外电源$v_0$，则$V_T^{+}=v_0$，$V_T^{-}=\frac{1}{2}{v}_0$

【注意：按我们上面这样接成的施密特触发电路是反相施密特触发电路】

3.用555定时器接成单稳态电路：

【应试技巧】：如果只有2作为输入端，那么就是单稳态电路。既然是单稳态电路，无非就是计算$t_w$
还记得我们在上一篇博文中强调的公式吗？$$T=RCln\frac{V_C(\infty )-V_C(0)}{V_C(\infty )-V_C(TH)}$$
我们可以看到，C是通过R和$V_{CC}$这条回路进行充电的，因此，$V_C(\infty )$ = $V_{CC}$，$V_C(0)$ = 0，对于$V_C(TH)$，我们得分析一下：对$C_1$, $v_{R1}=\frac{2}{3}{V}_{CC}$，假设C从t开始从0开始充电，一开始的一段时间里面$v_{I1}$是小于$v_{R1}$的，$C_1$输出为低电平，当电压慢慢增大，到刚刚好等于 $v_{R1}=\frac{2}{3}{V}_{CC}$，再增大一点点，$V_{C1}$立刻就跳变为高电平了，因此充电的阈值电压$V_C(TH)=\frac{2}{3}{V}_{CC}$

这样，三个参数都知道了，$t_w$便手到擒来

【注意一点】：我们这里用555定时器接成的单稳态电路，是在输入信号的下降沿到来时，电路进入暂稳态，此时，电容C从电压为0开始充电

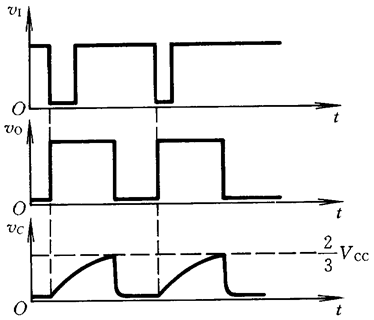
4.555定时器接成多谐震荡电路：

【应试技巧】：2，6脚连接在一起，没有输入的，就是多谐震荡电路
我们注意一下多谐震荡的波形：

【这里说明一下】：对于我们这里用555定时器接成的多谐震荡电路，我们画输出电压波形是根据电容C上的电压$v_C$，结合反相施密特触发电路的电压传输特性画出来的，（因为我们把555定时器接成多谐震荡电路就是在接成反相施密特触发电路的基础上变过来的）

我们无非就是计算T，充电时间$T_1$,放电时间$T_2$。
对于充电，是通过电源$V_{CC}$，$R_1$和$R_2$的回路充电的，$V_C(\infty )$ = $V_{CC}$；然后$V_C(0)$ = $\frac{1}{3}{V}_{CC}$ (这里要特别注意！！）；$V_C(TH)$ = $\frac{2}{3}{V}_{CC}$，那么充电时间$T_1$可以表示为：$$T_1=(R_1+R_2)Cln\frac{V_{CC}-\frac{1}{3}{V}_{CC}}{V_{CC}-\frac{2}{3}{V}_{CC}}=(R_1+R_2)Cln2$$

下面到了放电，我们知道放电放到尽头就是0嘛，因此，$V_C(\infty )$ = 0；$V_C(0)$ = $\frac{2}{3}{V}_{CC}$(特别注意！！）$V_C(TH)=\frac{1}{3}{V}_{CC}$,而放电的话是经过电阻$R_2$放电的，因此放电时间$T_2$可以表示为：$$T_2=R_{2}Cln\frac{0-\frac{2}{3}{V}_{CC}}{0-\frac{1}{3}{V}_{CC}}=R_{2}Cln2$$