Cluster analysis ：Basic Concepts and Algorithms -- Part 5 Cluster Evalation

系列文章

Cluster analysis ：Basic Concepts and Algorithms – Part 1 Overview
Cluster analysis ：Basic Concepts and Algorithms – Part 2 K-means
Cluster analysis ：Basic Concepts and Algorithms – Part 3 Hierarchical Clustering
Cluster analysis ：Basic Concepts and Algorithms – Part 4 Density-based clustering(DBSCAN)

---

关键词：
簇评估(Cluster Evalation); 监督(supervised) ; 非监督(unsupervised)
凝聚度(cluster cohesion) ; 分离度(cluster separation)
邻近度(proximity) ; 相似度(similarity)
邻近度矩阵(Proximity Matrix); 相似度矩阵(Similarity Matrix) ; 混淆矩阵(Confusion Matrix);
轮廓系数(silhouette coefficient) ; 相关性(Correlation); 聚类趋势(Clustering Tendency);
统计学(Statistics); 显著性(Significance) ;
熵(Entropy); 准确率(Accuracy); 纯度(Purity);
精度(Precision); 召回率(Recall); F度量(F-measure)

1 前言

前几节文章介绍了几种常见的不同的聚类方法，实际上每种聚类算法都会在数据集中发现簇，即使该数据集中根本没有自然簇（如随机的数据点），下图展示了三种聚类方法对随机数据点的聚类结果。因此对于聚类效果进行评价是必要的。
图1-1 不同的聚类算法从随机数据中找到的簇

对于聚类分析的评价，不仅仅是评估生成的簇的好坏那么简单，评估的目的在于：

• 避免将噪声识别为一定模式的簇（To avoid finding patterns in noise）
• 对比不同的聚类算法（To compare clustering algorithms）
• 对比两个不同的簇群（To compare two sets of clusters）
• 对比两个簇（To compare two clusters）

簇评估（Cluster Evalation），或者 簇验证（cluster validation)，最重要的任务之一就是：识别数据中是否存在非随机结构（non-random structure)，主要解决的几个重要问题：

• 确定数据集的聚类趋势（cluster tendency) ,是否存在非随机结构。
• 确定正确的簇个数 。
• 在不参考外部信息的情况下，评估聚类分析结果对数据的拟合情况。
• 将聚类分析结果同已经知道的客观结果（如外部提供的标号）对比。
• 对比两个簇集哪个更好。

第1-3项不使用外部信息，是内部非监督技术（internal unsupervised）；第四项是使用了外部信息（external），是监督技术(supervised）；第5项可以采用监督或者非监督的技术。随后将介绍监督（supervised）和非监督（unsupervised）的概念。

2 簇评估概述

评价指标一般分成三类：

• 非监督（unsupervised）：在不引入任何外部参考信息的情况下，来评价聚类结构的好坏。通常称作内部指标。
  ( Used to measure the goodness of a clustering structure without respect to external information; Often called internal indices because they only use information in the data )
  进一步可以划分成两类：
  （1）簇的凝聚度（cluster cohesion): 衡量簇中的对象之间的密切程度，例如SSE，簇内部的误差平方和。
  
  其中，ci是簇Ci的质心，x是簇Ci中的点。
  复习一下：误差的平方和（Sum of the Squared Error,SSE)：计算每个数据点的误差，即点到最近质心的欧几里得距离，然后计算所有误差的平方和。使得簇的SSE最小的质心就是均值。
  （2）簇的分离度（cluster separation): 衡量一个簇同其他簇的区别或者分离程度，例如SSB，簇之间的误差平方和。
  这里，mi是第i个cluster的大小，c是总体数据的质心。
• 监督的（supervised)：衡量聚类产生的簇标签同外部提供的类别标签的匹配度。通常称作外部指标。例如熵(Entropy）
  （Used to measure the extent to which cluster labels match externally supplied class labels; Often called external indices because they use information external to the data）
• 相对的（relative)。同时使用监督的和非监督的评价方法，来比较不同的簇或者聚类。例如利用SSE和熵（Entropy）来比较两个K-means。

3 非监督的簇评估

3.0 邻近度概念

复习一下邻近度（proximity）的概念：邻近度指的是两个对象之间的相似度（similarity）或相异度（dissimilarity)。

• 相似度（similarity）：衡量两个对象相似程度的数字度量，通常在0（不相似）和1（完全相似）之间。常见的相似度，如余弦相似度cosine, 相关性指标correlation，Jaccard指标, Rand简单匹配系数等。
• 相异度（dissimilarity）：又称为距离，衡量两个对象差异程度的数值度量，对象越类似相异度越低。常见的距离函数如欧几里得距离，曼哈顿距离等。
• 相似性和相异性之间可以进行转化。s作为相似度符号；d作为相异度符号。可使用公式s = 1−(d−min d)/(max d−min d)将距离转化成相似度。

3.1 使用凝聚度和分离度

对于不同的聚类，使用不同的有效性评价指标。对于划分的聚类，簇有效性评价多基于凝聚度和分离度。

3.1.1 基于图的凝聚度和分离度

回顾一下，基于图的簇（Graph-Based clusters）。簇内的点互相连通但不与簇外的对象连通。如基于邻近的簇（contiguous clusters/ Nearest neighbor or Transitive）。基于邻近的簇适用于当不规则或者缠绕的簇。

邻近度图：每对数据点之前有一条连线，赋予这个连线一个权重，该权重是两个数据点之间的邻近度。

使用邻近度图的方法来计算凝聚度和分离度：

• 簇凝聚度（Cluster cohesion）是簇中点与点之间所有连线的加权和。
  
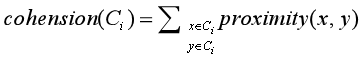
• 簇分离度（Cluster separation)是簇中的节点和簇外部的节点之间距离的加权和。