一次二阶矩法

一次二阶矩法

非线性功能函数g(x)展开成泰勒级数保留一次项，按照可靠指标形成求解方程，可以得到求解可靠度的一次二阶矩法。此方法简单、常用、易于掌握。
一次二阶矩法分中心点法和设计验算点法。中心点法不考虑随机变量的概率密度分布（不足）。

设计验算点法

原理

设独立正态分布变量组合为结构极限状态方程及极限状态面上的一点，在该点按泰勒级数展开保留一次项，得

同时可以得到的均值以及标准差


结构可靠性指标为

令

处于极限状态面上及值为0，且把Xi用标准化变量替换，并除以得到

令

由上面推导，上式可整理成：

该方程为Y空间内的法线式超平面方程如图（二维情形），可靠度指标β为该空间内坐标原点到该极限状态面的最短距离，p*点称为设计验算点

设计验算点在Y空间中的坐标为

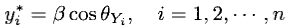
转化为原始空间的坐标为

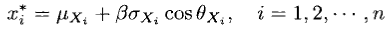
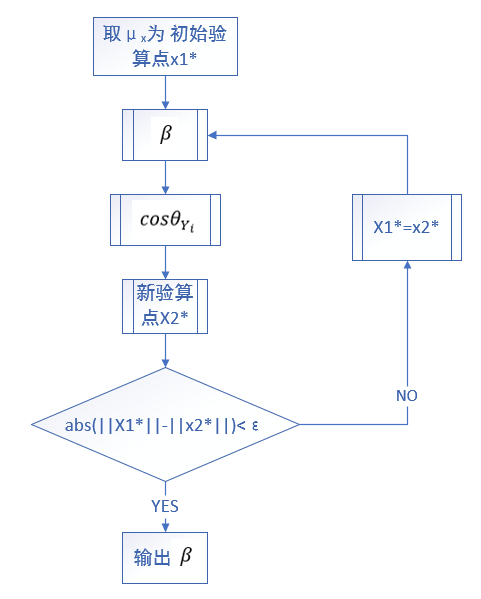
可以利用如下迭代方法得到可靠度指标β

当量正态法(JC法)

当处理的X变量为非正态分布时，我们可以把它处理成相应的当量正态化变量X‘。JC法中进行该处理需满足在验算点处和的累积分布函数和概率密度函数分别对应相等，即

则当量正态化变量的均值和标准差为：

完成替换以后，我们就可以利用前面所述方法求得相应的可靠度指标。

映射变换法

该方法的思想是利用累积分布函数值相等的映射，将非正态分布随机变量变换为正态分布随机变量。
对于随机变量有概率密度函数和累计分布函数，我们可以作一定变换（等概率变换）将它映射为标准正态变量Y：

由此可得

其中Y是标准正态向量，且可以推导出：



其中

同前面，我们可以用该方法，把其他分布的变量转化为标准正态变量。然后运用第一节方法得到结构可靠度指标。基本流程如下：