定点乘法器----基4booth算法

一. 简介

本篇文章将介绍如何使用 基4 booth算法(赛题中介绍了)来生成部分积，在开始之前，简要介绍一下定点乘法器的计算流程:

对乘数进行booth编码 —> 利用得到的编码值和被乘数生成部分积 ----> 对部分积进行压缩求和。

基4 booth(后面简称为booth2)算法用来完成前面的两步。

ps: 有booth2就有booth1，它们大同小异，只不过booth1太垃圾了，感兴趣的可以自行了解。

二. booth2 编码

编码的过程很简单，将乘数的末尾补个0，然后三位三位为一组，通过公式计算出对应的值即可。如下图，末尾的0是补的，对8bit乘数来说，可以生成出4组数据。

然后将这4组数据，应用下面的这个公式，便可得到最终的4个编码值。

得到编码值之后，用每个编码值去乘以被乘数得到部分积，将部分积末尾不错对应数量的0即可。

编码值a，不需要补0，编码值b需要补充2个0，此时位宽为10bit，编码值c需要补充4个0，此时位宽为12bit,以此类推即可。

最后将部分积的符号位扩展一位即可，例如正数的符号位为0，那么就用00表示，负数的符号位为1，那么就用11表示。

boot2编码就这样完成了它的任务，至于为什么可以这样，可以参考下面的公式，来源于赛题，看懂就可以知道那个编码公式怎么来的了，以及补0操作(左移对应位数)，非常简单是吧。

三. booth2 编码代码实现

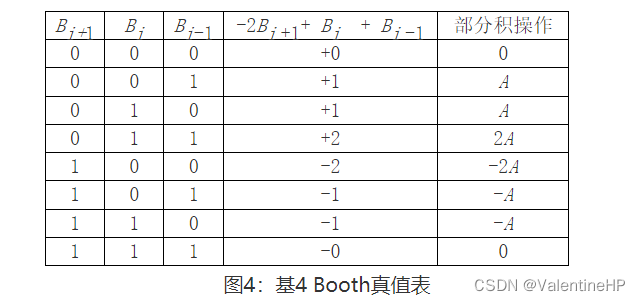
通过booth2编码的真值表可以知道

组数为 000 或者 111 时 ，部分积为0

组数为 001 或者 010 时， 部分积就是被乘数

组数为 011 时， 部分积就是被乘数左移动一位

组数为 100 时，部分积就是被乘数左移动一位，然后取相反数

组数为 101 或者 110 时，部分积为被乘数的相反数。

总结可以发现，当组数的最高位为0时，被乘数不变，当组数的最高位为1时，需要对被乘数取反，当组数的最后两位一样的时候，那么就需要对被乘数左移一位的操作。那么可以使用如下三个变量进行标记，当set0为1时，直接输出0,不用判断其他两个变量，否则需要判断。完整代码如下。

四. 部分积生成代码实现

首先，需要提前计算三个值-A,-2A,2A。

然后按照上面分析的，来生成部分积，这里将部分积扩展到了32bit，因为16bit乘16bit，结果的最大位宽为32bit。只截出了两个部分积，其余部分积依次类推。

至此 基4 booth算法介绍完毕，实现过程没有经过任何优化，和算法可以清晰对应上。当然，提前透露一下，最终效果延时比较高，效果不是很好，效果如图。

关注回复 ： 定点乘法器基础版本
获取完整代码

下一篇，将介绍部分积的压缩。