计算机图形学九重心坐标及其应用

重心坐标及其应用

重心坐标在计算机图形学当中极为常用。
知道三角形的三个顶点的属性，便可插值出其内部任意一点的对应属性。比如当深度缓存时，高洛德着色时，我们都用到了重心坐标公式。

直线上的重心坐标

直线AB上任意一点，都可以表示为P = (1-k)A+kB（0<k<1)时，该点在直线AB中间。当k大于1，或者是k小于0时，点依然会在AB上，但是是在两点之外了。
我们令m=1-k，令n=k，就可以得到P=mA+nB (m+n=1)，所以在已知AB的情况下，我们可以用m，n的坐标来表示直线上的任意一点，这也就叫做直线上的重心坐标。

三角形上的重心坐标

类比直线，三角形也存在重心坐标。与直线上一点满足P=mA+nB (m+n=1)一样，三角形所在平面上任意一点的坐标可以表示为P = mA+nB+kC (m+n+k=1)的形式，其中，当0<=m,n,k<=1时，该点在三角形内及三角形边上。
三角形重心的几何意义可以看做是三角形内一点，连接三个顶点，顶点所对的三角形占总三角形的面积。就是该点的重心坐标。

当点在某个边的外侧时，该点与边构成的三角形的面积计算为负值。

应用场景

我们知道了我们可以通过重心坐标来计算三角形内任意一点的坐标。那这有什么用呢？
我们不止可以把三角形顶点的位置进行插值计算出任意一点的坐标。还可以将顶点的其他属性，如颜色，法线，uv坐标，深度等，套重心公式插值得到三角形内任意一点。
所以我们只需要先通过四个点的位置信息算出重心坐标，之后即可通过重心坐标来计算其他属性的插值。

重心坐标与投影

重心坐标的计算只和x，y，z当中的任意两项有关，在计算机图形学中，主要用到的是重心坐标的平面概念。到底是用的哪两项呢，具体是看我们三角形的投影平面是由哪两项来表示的。

通常来说，三角形的重心坐标不需要考虑z的值，因为空间中的重心在平面上的正交投影上，重心的投影依然是三角形的重心。所以说不用考虑z值，只插值x，y值即可。
如下图，D在与投影平面正交投影后，依然在直线的中心，比例关系没有改变。

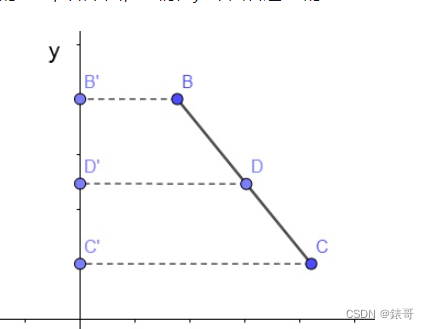
但是上述条件只存在于正交投影，我们知道在mvp变化时，p变化矩阵可以是透视投影矩阵，因此重心的表现形式就不能忽略z的影响。看下图：

上图可以看出，此时的投影光线与投影平面并不平行，D点也从平分B,C两点变成了偏向c，不再平分。
这里应该有一大堆数学证明。
可以参考下面的文章：
https://zhuanlan.zhihu.com/p/361943207
https://zhuanlan.zhihu.com/p/144331875

矫正：

用这个公式去插值,自己手打的。。。zt是插值点的深度，I是插值点的属性，zazbzc是插值点的深度，知道四个点的深度，和顶点的属性，还有重心坐标，插值出所求点的对应属性。

其实就是z坐标，本来是有线性关系的，但是经过透视投影变换后，失去了线性关系，因此需要进行一个矫正。