巢式病例对照研究，发表一区文章，IF=9.9-CSDN博客

9.23-24 郑老师“量表与中介研究数据分析”课程（回放录屏）

2023年7月，巴黎萨克雷大学学者在《Neurology》（一区，IF=9.9）发表题为：" Association of Physical Activity and Parkinson Disease in Women: Long-term Follow-up of the E3N Cohort Study" 的研究论文。

这项研究使用的数据来自“1990年至2018年国家教育女性健康病学研究”，目的是研究时变体力活动(PA)和女性帕金森病(PD)之间的关系。使用潜在过程混合模型创建了一个时变的潜在PA (LPA)变量。建立了一个巢式病例对照研究，使用具有回顾性时间尺度的多变量线性混合模型来检查LPA轨迹的差异。采用Cox比例风险模型估计时变LPA和PD发病率之间的关系。总的来说，较高的PA水平与较低的女性PD发病率相关，不能用反向因果关系解释。这些结果对于PD预防的干预计划具有重要意义。

摘要与主要结果

一、摘要

背景：先前的队列研究报道，在基线时评估的单一体力活动(PA)测量与较低的帕金森病(PD)发病率相关，但一项荟萃分析表明，这种关联仅限于男性。由于疾病的前驱期较长，不能排除反向因果关系作为一种潜在的解释。我们的目的是研究时变PA和女性PD之间的关系，使用滞后分析来解决潜在的反向因果关系，并比较诊断前患者和匹配对照组的PA轨迹。

方法：我们使用的数据来自“1990年至2018年国家教育女性健康病学研究”，这是一项针对参与国家教育工作者健康保险计划的女性的队列研究。在随访期间，患者在6份问卷中自我报告了PA。随着问卷中问题的变化，我们使用潜在过程混合模型创建了一个时变的潜在PA (LPA)变量。PD是通过基于医疗记录的多步骤验证过程或基于药物声明的验证算法确定的。我们建立了一个巢式病例对照研究，使用具有回顾性时间尺度的多变量线性混合模型来检查LPA轨迹的差异。采用Cox比例风险模型，以年龄为时间尺度，并对混杂因素进行调整，以估计时变LPA和PD发病率之间的关系。我们的主要分析使用了10年的滞后来解释反向因果关系;敏感性分析使用了5年、15年和20年的滞后期。

结果：轨迹分析(1196例病例和23879例对照)显示，在整个随访期间，包括诊断前29年，病例的LPA显著低于对照组;在诊断前10年，病例和对照组之间的差异开始增加(p相互作用= 0.003)。在我们的主要生存分析中，2000年95,354名无PD的女性中，1,074名女性在平均17.2年的随访中患上了PD。PD发病率随着LPA的增加而下降(p趋势= 0.001)，最高四分位数的发病率比最低四分位数的发病率低25%(校正风险比0.75,95% CI 0.63-0.89)。使用更长的滞后时间也得出了类似的结论。

结论：较高的PA水平与较低的女性PD发病率相关，不能用反向因果关系解释。这些结果对于PD预防的干预计划具有重要意义。

二、研究结果

1.图1显示了将参与者纳入研究的流程图。我们排除了50例可能的PD病例，13例没有诊断日期的病例，31例Q1流行病例，229例未在任何问卷中回答PA问题的女性;在其余的E3N参与者中，90%在随访期间有3个或更多的PA测量，其中80%有5或6个可用的测量。

可用于生存分析的参与者数量随着滞后时间的增加而减少。例如，在我们的主要生存分析(10年滞后)中，我们进一步排除了2000年之前随访结束的3193名女性和125名流行PD患者，留下95,354名女性随访19年(平均= 17.2,SD = 3.3)，其中1,074名女性发展为PD。与以往研究相比，本研究纳入PD患者人数最多，随访时间最长(表2,links.lww.com/WNL/C801)。

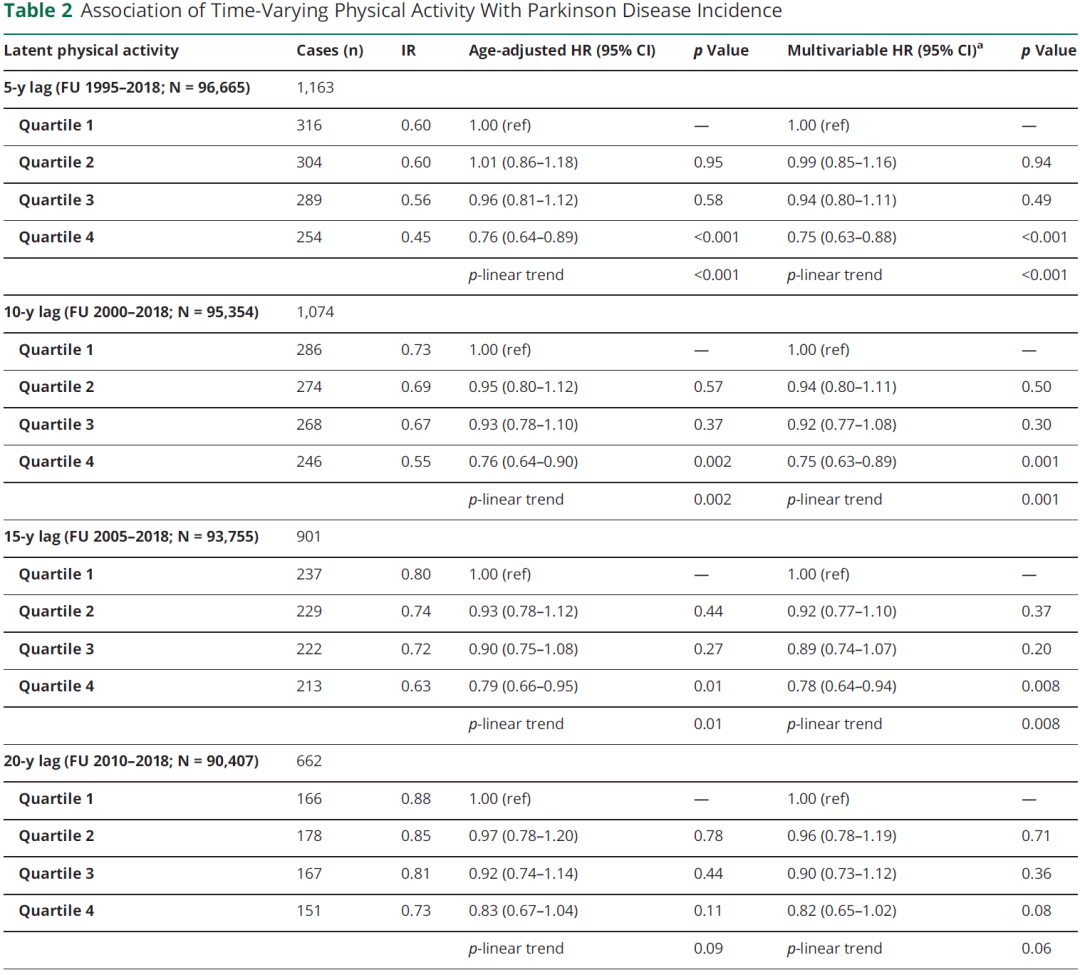
FU =随访;HR =风险比;IR =每1000人年帕金森病的年龄标准化发病率。

HR和95% CI采用Cox比例风险模型以年龄为时间尺度计算时变变量。

a根据基线居住地(农村/城市)、初潮年龄(≤11/12-13 /≥14岁)、胎次(未生育/1个孩子/2个孩子/≥3个孩子)、随时间变化的吸烟(从未/曾经/现在)和绝经状态(绝经前/自然绝经/人工绝经/未知类型的绝经)对模型进行调整。

表1描述了基线(1990-Q1)参与者的特征。平均年龄49.3岁(SD = 6.6)，平均PA水平为45.3 (SD = 30.1) METs-hour/week。初潮年龄较晚、有3个以上子女以及生活在农村地区的妇女LPA水平高于同龄妇女。与未患PD的女性相比，患PD的女性年龄更大，吸烟更少，绝经后更频繁，月经初潮年龄更晚，孩子≥3个的女性更多(表3,links.lww.com/WNL/C801)。

BMI =身体质量指数;LPA =潜伏性PA;MET =任务代谢当量;PA =体力活动。

基线特征显示了基于5年滞后的参与者的生存分析。

a.1169名女性(1.2%)在基线时没有PA;因此，我们在这些妇女的随访中使用了第一个可用的LPA值(95%在1993年第3季度或1997年第5季度)。

b.基线问卷评估的总PA (1990-Q1)。

c.在随访结束时进行评估。

2.PA在PD之前的轨迹

在纳入巢式病例对照研究的25,200名女性(1,200例和24,000例年龄匹配的对照)中，我们排除了45名女性(4例PD病例)，这些女性在T0之前的所有就诊中都没有PA，并排除了80名与这4例PD病例匹配的对照，最终样本为25,075名女性(1,196例PD病例和23,879例对照);1156例与20例对照，39例与19例对照，1例与18例对照。

e表4 (links.lww.com/WNL/C801)描述了在索引日期(T0)时病例和对照的特征。病例和对照组的平均(SD)年龄为71.9岁(SD = 7.8)。与对照组相比，PD患者吸烟和肥胖的发生率较低，月经初潮≤11年或≥14年及人工绝经的发生率较高，生育子女较多。图2显示了病例和对照中最常见的协变量和3个年龄的LPA轨迹;e表5 (links.lww.com/WNL/C801)给出了相应模型的估计数。

病例和对照组的LPA在初始升高后，在T0之前的10年里，由于PD状态和时间之间存在显著的相互作用(p相互作用= 0.003)，病例的LPA下降幅度大于对照组。病例在T0时的PA水平显著低于对照组(差异为- 0.164,95% CI为- 0.230至- 0.097);这种差异在T0之前的10年里有所下降，但在整个随访过程中仍然很显著，病例的LPA明显低于T0之前29年的对照组;因此，在索引日期，病例和对照组之间的LPA差异比研究开始时更大。基于这些发现，我们使用了10年的滞后时间来进行主要的生存分析。

此外，LPA水平随着年龄的增长而下降，随着孩子的数量而增加，吸烟者的LPA水平低于不吸烟者，城市地区的LPA水平低于农村地区的LPA水平，绝经后妇女的LPA水平低于绝经前妇女。

图A.a、B.a和C.a显示了1196例PD患者和23879例对照患者的平均LPA轨迹(95% CI)，该轨迹基于具有回顾性时间二次函数的线性混合模型;模型系数如表5所示(links.lww.com/WNL/C801)。图A.b、B.b和C.b显示了PD病例和对照组潜在身体活动平均轨迹之间的差异(95% CI)。CI不包括0(水平虚线)的差异具有统计学意义。我们采用回顾性时间量表，T0(时间= 0)代表病例的PD诊断年份，对照组的索引日期。对模型进行了PD状态、T0时年龄以及时间与PD状态和T0时年龄的双向相互作用调整。进一步调整了基线胎次、居住地、初潮年龄、随时间变化的吸烟和绝经状态。考虑到年龄和时间之间的显著相互作用，绘制了3个不同年龄(63,73和83岁)和E3N参与者最常见的特征(从不吸烟，12-13岁初潮年龄，自然绝经，2个孩子，生活在城市地区)的轨迹。E3N = Etude Epid ' emiologique aupr 'es de femmes de la Mutuelle Generale de l 'Education Nationale;LPA =潜在体力活动;PD=帕金森病。

3.PA和PD的发生率

图3显示了PD在随访期间的CIF，同时考虑了竞争死亡风险;LPA最高四分位数的女性与最低四分位数的女性相比，CIF降低了22% (95% CI 7%-34%， p = 0.007)。

表2显示时变LPA与PD发病率之间的关系。在我们的主要分析(10年滞后)中，PD的风险随着PA的增加而降低(p趋势= 0.001)，最高四分位数的发生率比最低四分位数的发生率低25% (HR 0.75, 95% CI 0.63-0.89)。随着PA水平的升高，PD的危险性呈线性降低;基于样条的分析没有偏离线性(p = 0.25;图4)。使用更长的滞后时间也产生了类似的关联(表2);在PD病例数较少的情况下，这种负相关在20年的滞后中具有临界显著性(p趋势= 0.06)。

对地中海饮食、咖啡因和乳制品摄入进行调整后的敏感性分析(表3)或排除基线PA评估(e表6,links.lww.com/WNL/C801)得出了类似的结果。按中位年龄分层的分析显示，两个年龄组的相关性相似(e表7)。在使用替代PD定义的分析中，相关性与我们的主要分析相似(e表8)。在调整了代表潜在介质的合并症(BMI，高血压、高胆固醇血症、糖尿病和心血管疾病)，在调整这些协变量后，PA和PD之间的关联保持不变，这些协变量解释了PA和PD之间关联的一小部分(5.5%)(e表9)。

PD作为第一季度(1990)评估的LPA四分位数的函数的累积发生率函数，通过竞争风险的Fine-Gray回归模型进行预测，以随访开始以来的时间作为时间尺度，并有10年的滞后(随访，2000-2018)。模型调整了年龄(3节的限制三次样条)、胎次、居住地、初潮年龄、吸烟和绝经状态(所有在随访开始时评估)。LPA =潜在体力活动;PD=帕金森病。

HR和95% CI采用以年龄为时间尺度的时变变量的Cox比例风险模型计算，并根据基线居住地(农村/城市)、初潮年龄(≤11/12-13 /≥14岁)、胎次(未生育/1个孩子/2个孩子/≥3个孩子)、时变吸烟(从未/曾经/现在)和绝经状态(绝经前/自然绝经/人工绝经/未知绝经类型)进行调整。

点对应LPA四分位数与参考四分位数的HR(表2)及其95% CI(竖线);hr在每个四分位数的中位数绘制。橙色实线表示作为线性变量建模的连续LPA的PD HR，阴影区域对应95% CI。随着LPA水平的升高，PD的HR呈线性下降。绿色实线表示用受限三次样条建模的连续LPA的PD HR，阴影区域对应95% CI;3节提供最佳配合(较低的AIC值)。没有明显偏离线性(p = 0.25)。

赤池信息准则;HR =风险比;LPA =潜在体力活动;帕金森病。

设计与统计学方法

一、研究设计

P（Population）参与者：来自E3N队列研究的98,995名出生于1925年至1950年并于1990年招募的法国女性。

E（exposure）暴露因素：体力活动（PA）。

O（outcome）结局：帕金森（PD）发病率。

S（Study design）研究类型：巢式病例对照研究。

二、统计方法

1.采用SAS 9.4 (SAS Institute Inc.，Cary, NC)、lcmm R软件包(R Foundation for Statistical Computing, Vienna, Austria)、24和Stata 15.1 (StataCorp, College Station, TX)进行统计分析。

2.潜在PA过程

当风险因素的测量工具在后续过程中发生变化时，潜在过程混合模型(LPMMs)允许包括来自不同测量工具的观察结果，并定义潜在过程的轨迹，前提是这些工具测量相同的量。这个潜在过程代表了通过不同工具获得的观测结果背后的不可测量的共同因素。我们的目的是使用LPMMs预测来自至少有1次PA评估的队列(N = 98,766)的所有参与者的潜在PA (LPA)过程。

为了将从不同问卷中获得的重复个体PA测量值(以小时/周为单位)与它们共同的潜在过程联系起来，并纠正每个活动偏离正态分布，我们首先根据活动特异性LPMMs中的Akaike信息准则(AIC)选择最佳活动特异性参数化链接函数(在2、

3、4和5节的二次i样条链接函数中)。然后，我们将11个活动(具有先前确定的活动特定链接函数的形状)纳入同一LPMM中，用于多变量纵向结果，以根据年龄建立LPA轨迹模型。年龄以Q1(49岁)的平均值为中心，随年龄的变化由2个内节的自然三次样条曲线(较低的AIC)近似表示。参与者内的相关性通过独立的随机截距和年龄的3个函数的斜率来捕获。

我们最终基于最佳拟合LPMM获得了每位患者每次就诊时的患者特异性LPA预测，并将其用于随后的轨迹和生存分析。

由于依赖于极大似然估计，LPMM允许在随机缺失的假设下处理PA的缺失值，即可以通过PA的观测值和其他协变量(年龄)来预测给定时间点的缺失值。

3.LPA在病例和对照组中的轨迹

使用线性混合模型对病例和对照组进行了29年随访，从指标时间T0到研究开始(回顾性时间尺度)的LPA轨迹进行了检查。LPA轨迹建模为回顾性时间和时间平方的函数，并根据PD状态、T0时年龄以及时间与PD状态和年龄的双向相互作用进行调整；进一步调整了与PA和PD相关的混杂因素，包括胎次、月经初潮年龄、农村居住、随时间变化的吸烟和绝经状态参与者内部的相关性通过相关的随机截距和时间和时间平方的斜率来捕获。

4.生存分析

我们使用Cox比例风险模型对时变变量以年龄为时间标度来估计风险比(hr)、95% ci和双尾p值(α = 0.05)。

为了解决反向因果关系的可能性，我们在时变变量(包括LPA)和PD发病率之间纳入了持续时间增加的滞后(5、10、15和20年)。鉴于上述轨迹分析的结果，我们在主要分析中使用了10年的滞后时间:LPA滞后了10年，我们在2000年开始随访(即基线评估后10年)，因此在2000年之前患PD的参与者(流行病例)被排除在外。这些女性从2000年开始随访，直到PD诊断或随访结束(最后一次问卷调查和最后一次药物报销的最长日期)。同样的方法也用于其他滞后。

LPA作为时变四分位数纳入模型，并通过每个四分位数的中位数定义的有序变量来检验hr的线性趋势。我们还使用限制立方样条来测试连续LPA的线性偏离。分析调整了与PA和PD相关的混杂因素，包括基线胎次、初潮年龄、农村居住、随时间变化的吸烟和绝经状态缺失值被编码为特定类别，以保留所有分析中相同数量的参与者。

在存在竞争死亡风险的情况下，我们使用Fine-Gray亚分布风险模型来估计PD随时间的累积发生率函数(CIF)在这项分析中，我们估计PD的CIF是第一季度LPA四分位数的函数，以随访开始以来的时间为时间尺度，滞后10年。根据上述协变量和随访开始时的年龄(3节限制立方样条)对分析进行调整。

5.敏感性分析

（1）我们通过排除基线PA问题(1990-Q1)构建了一个替代的LPA变量，这些问题比随后的测量方法更不精确。

（2）为了检查我们的发现是否可能与饮食混淆，我们根据第5季度(1997年)评估的PA进行了分析，并调整了在随访期间早期评估的与PD风险相关的饮食暴露(1993-Q3;地中海饮食，咖啡因和奶制品的摄入)由于病例数量不足，不可能进行滞后超过10年的分析。

（3）我们对中位年龄(72.8岁)进行了分层分析，以检查在该年龄之前或之后发展为PD的PD患者的相关性是否相似。

（4）为了检验病例定义对我们研究结果的影响，我们排除了算法预测的PD患者，并对基于医学文献(明确或可能;定)。因为我们担心减少的样本量会导致统计能力不足，所以我们进行了额外的分析，除了经过验证的病例外，我们还保留了基于更具体版本的算法(90%灵敏度;特异性为90%)。在这些分析中，我们比较了第四个四分位数的PD发病率与其他三个四分位数的发病率之和。

（5）高PA与一些合并症的风险较低相关，包括肥胖、高血压、血脂异常和心血管疾病因此，合并症可能是PA和PD之间关联的潜在媒介。我们对随时间变化的BMI和高血压进行了敏感性分析，研究高胆固醇血症、糖尿病和心血管疾病对PA和PD之间关系的影响。