潜类别分析（LCA）了解一下？它把多个分类指标变成一个分类指标

欢迎投稿！ 诚寻兼职作者！不妨来分享你们的科研干货！

摘要：这是一篇高质量长文，感兴趣的朋友可以收藏起来慢慢读。该文详细介绍了潜在类别分析是什么，还通过一篇核心论文分析了其在医学科研领域中的用法，最后还直接给出了详细的实操代码，希望能为大家的研究提供助力。

一、潜在类别分析是什么？

在回答这个问题之前，我尝试将这个问题抛给大模型，它的答复如下：

---

“潜在类别分析（Latent Class Analysis，LCA）是一种统计方法，用于探索存在统计学关联的分类外显变量背后的类别潜在变量。它是潜在变量模型的一种，主要应用于分类变量。

在LCA中，潜在变量是不可观测的类别变量，而外显变量是可观测的类别变量。LCA的基本假设是，对于各个外显变量，其各种反应的概率分布可以由少数互斥的潜在类别变量来解释。每种类别对各外显变量的反应选择都有特定的倾向。

LCA的目的在于利用最少的潜在类别数目解释外显分类变量之间的关联，并使各潜在类别内部的外显变量之间满足局部独立的要求。也就是说，它试图找到一个潜在的类别结构，使得该结构能够最好地解释外显变量之间的关联。

LCA的应用范围非常广泛，包括市场研究、心理学、社会学、医学和生物统计学等多个领域。它可以用于探索性数据分析，如识别不同的群体或行为模式，或者用于验证性数据分析，如检验某种假设或模型的有效性。

需要注意的是，LCA的结果可能受到多种因素的影响，包括潜在类别的数量、潜在类别与外显变量之间的关系、样本大小和数据质量等。因此，在进行LCA之前，需要对数据进行适当的预处理和检查，以保证分析的可靠性和有效性。”

---

根据上面的回复，不难发现，LCA是潜变量模型的一种，稍微难理解的概念可能就是“潜在类别”。

潜在的意思是指潜变量，这是个与外显变量对立的概念，由于我们之前在结构方程模型的相关学习中了解过，这里就不细说了。有兴趣的可以点击链接：在吗？这是一份关于结构方程模型的修炼手册

为了帮助大家理解“潜在类别”，举个简单例子（参考自温忠麟老师等发表的论文）。

“某学校近期进行了一场学业测验，试卷只有两道题目（假设的），两个题目得分对应于两个类别变量，分别记为X1和X2。X1为4级计分，有4 种可能的取值，即(0,1,2,3)。X2有3 种可能的取值(0，1，2)。

那么，这些学生可以被分成 4x3=12 类得分模式(更规范的说法：反应模式)。例如(0.0),(0,1),.,(3,2)，有的类别可能没有学生归属。也可以按两题得分之和(0至5分)将学生分成6类。

但是，请试想一下，如果题目更多或者每题分值更大，怎么办？没错，无论按反应模式还是总分来分类，最终划分的类别数量都可能很多。有没有更加简洁的分类方法？当然，完全可以将学生分成高、中、低学业水平三类。这种分类法很好用，并且还比较容易解释结果。

换成完整的考试试卷（比如数学），上述高中低分类模式，就可以理解为：高学业水平的学生可以正确回答不同难度的题目，中等水平的学生能正确回答比较简单的题目以及部分比较难的题目，而低学业水平的学生只能正确回答比较简单的题目”。

正是因为这些学生在回答不同难度的题目中表现出来的某种相似性，所以可以划分类别，这就是潜在类别分析的原理。此时，直接根据反应模式分类得到的是显类别，而根据反应模式简化分成的高、中、低类别就是潜类别。

现在是不是理解潜在类别了？心细的朋友可能就会发现了，这个LCA与我比较早的时候介绍过的潜在剖面分析（LPA）非常相似，不记得的话可以再看看我之前分享的推文，有通俗易懂的介绍，也有对新人友好的R语言LPA建模实操（相比于mplus，友好得不止一点点）：

1、问卷分析新选择——潜在剖面分析 

2、国内少见？没关系，手把手演示怎么用R做潜在剖面分析

没错，LCA与LPA同属潜在类别模型，两者都是根据个体在观测指标（可以是问卷的题目，也可以是其他能直接观测到的数据）上的不同反应模式将其进行分类，从而达到识别群体异质性的一类统计方法。

LCA与LPA就像双胞胎一样，同根同源，主要的区别在于潜在剖面分析（LPA）中的外显变量是连续变量（计量资料），而潜在类别分析（LCA）中的外显变量是类别变量（分类资料）。

LCA本质是基于概率的模型，涉及到的内容比较多，包括条件概率、全概率公式、贝叶斯公式、类别变量的联合分布与边际分布，我个人的理解也不是特别深入，所以LCA的数据模型就不列了，接下来我们看看论文与实操。

二、分析实例

上面的例子都是针对学校的学生，属于心理与教育领域，那么有没有直接用在护理领域的实例？有的，而且最近几年越来越多了。下面，举个发表于《解放军护理杂志》的文献。该文献得到了多项基金的支持：国家社会科学基金项目(18BGL248、20CGL 253);兰州大学中央高校基本科研业务项目(lzujbky-2020-10);兰州大学护理学院2020年科研项目(LZUSON202008)

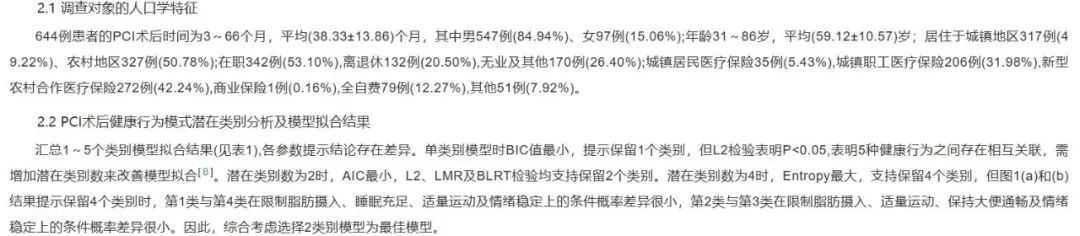
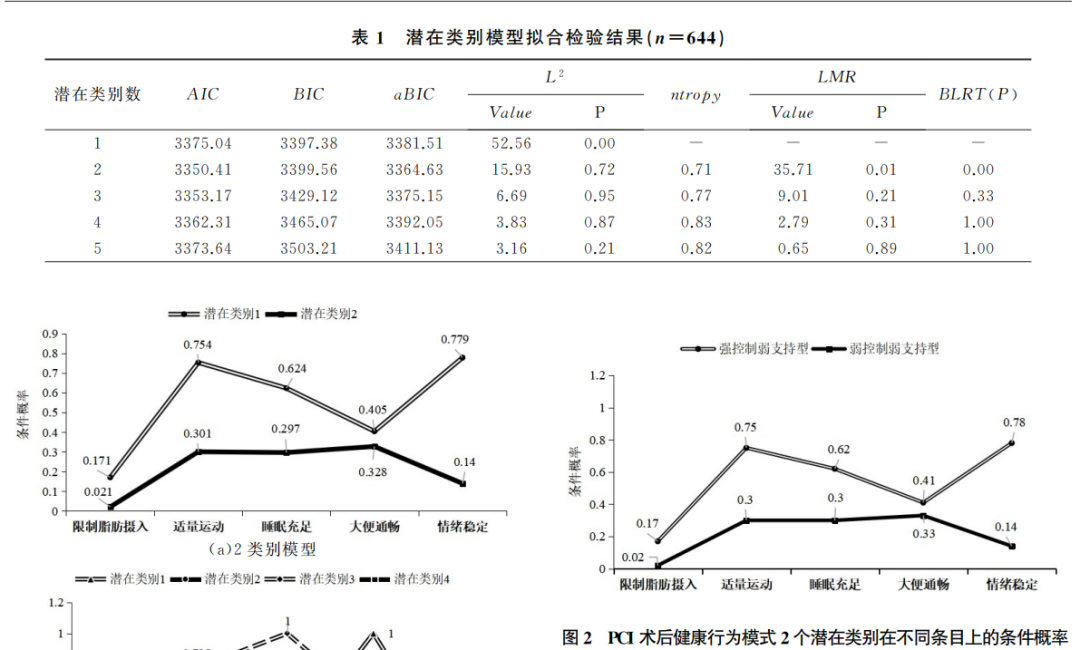
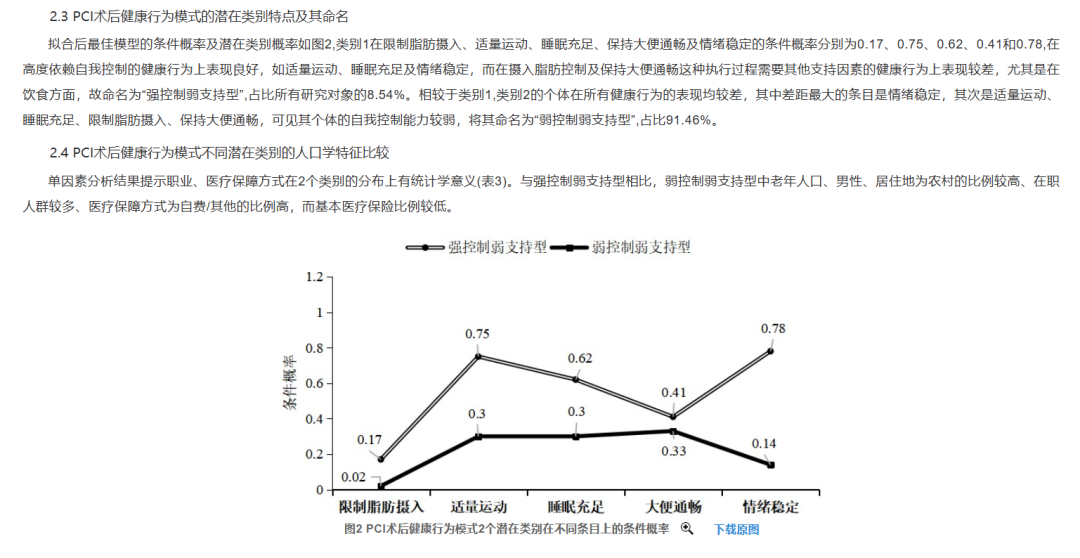
可见，作者通过比较分多个潜在类别时模型的拟合程度、AIC、BIC、似然比检验等指标，最终确定了一个分为2个类别的最优模型。

然后，以潜在类别为因变量，进行了单因素和多因素Logistic 回归分析。下面我们简单看看单因素分析和多因素分析的结果。其余内容不贴了，感兴趣的同学可以去看看原文。

该文的思路很清晰，不过是否有同学注意到作者是通过mplus软件做的LCA？不是说mplus不好，我用过一段时间，挺好的软件。只不过，很多研究者并不清楚，R软件也有一套很方便的LCA做法（与潜在剖面分析一样方便），几行代码轻松搞定。

人生苦短，我用R语言！跟我一起看看吧。

三、R语言快速搞定LCA

1、数据集

直接用R包作者给的示例数据包。

# 首次使用请先安装
# 安装代码：install.packages('poLCA')




#导入包
library(poLCA)


#导入数据集
data(election)


# 查看数据集
str(election)
View(election)

这是一份2000年美国全国大选研究的调查数据，样本量为1785。内容是询问受访者对总统候选人阿尔·戈尔和乔治·W·布什的各种品质(道德、关怀、知识渊博、好领导、不诚实、聪明)的看法。

共两组（两个候选人），每组六个问题，共12个题目。每个题目4个选项，回答是: (1)非常好; (2)还不错， (3)不太好; (4)一点都不好。

许多受访者对这些变量有不同数量的缺失值。数据集还包括潜在的协变量VOTE3，被访者2000年的投票选择(当被问及时)年龄，被申请人的年龄，Educ被申请人的教育水平;性别，被访者的性别，以及其他。

2、建立多个潜在类别模型

可以看到，该数据集有不少缺失值，不过不用担心，poLCA包下的poLCA函数有默认的缺失值处理方式，可以直接拟合LCA模型。

将所有的12个题目都纳入response，定义表达式：

# 先定义表达式，形式是response ~ predictors.
formula=cbind(MORALG,CARESG,KNOWG,LEADG,DISHONG,INTELG,
           MORALB,CARESB,KNOWB,LEADB,DISHONB,INTELB)~1

再拟合模型：

# 分别拟合class数量=1，=2，=3时的模型，
# 原理与潜在剖面分析差不多          
mod1 = poLCA(formula,election,nclass=1)  
mod2 = poLCA(formula,election,nclass=2)  
mod3 = poLCA(formula,election,nclass=3)

3、结果

输出的结果很多，分别对每个模型截取部分结果，

mod1的结果如下：

mod2的结果如下：

mod3的结果节选：

大部分需要汇报的LCA关键数据包含在里面了，比LPA的操作还要简单。

我们可以根据上面输出的结果筛选最优模型，然后进行后续分析。

4、绘制三维图（条件概率分布图）

plot(mod1)
plot(mod2)
plot(mod3)

上面是单个的。把3个类别放一起看看。

与Mplus软件的绘图比较一下：

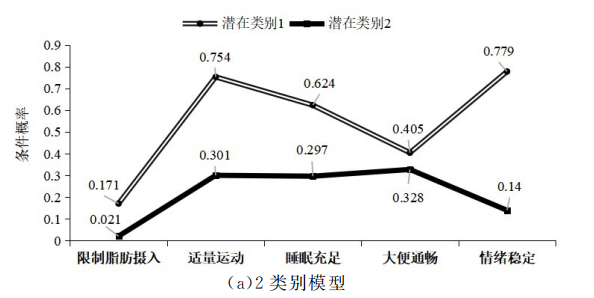
5、关键来了!

怎么输出每个样本的所属类别呢？没有这个类别划分的话，我们很难继续后续分析（比如多因素logistic分析）。执行下面的代码：

mod3$predclass#获取预测的类别

还可以将其保存下来，文件命名为‘lca.csv’。

write.csv(lc3$predclass,'lca.csv')

文章比较长，看到这里很不容易，很棒！本次分享到这

---

本公众提供各种科研服务了！

一、课程培训 2022年以来，我们召集了一批富有经验的高校专业队伍，着手举行短期统计课程培训班，包括R语言、meta分析、临床预测模型、真实世界临床研究、问卷与量表分析、医学统计与SPSS、临床试验数据分析、重复测量资料分析、nhanes、孟德尔随机化等10门课。如果您有需求，不妨点击查看： 发表文章后退款！2023年郑老师团队多门科研统计直播课程，欢迎报名 二、统计服务 为团队发展，我们将与各位朋友合作共赢，本团队将开展统计分析服务，帮忙进行临床科研。欢迎了解详情： 医学统计服务| 医公共数据库论文一对一指导