stata 蒙特卡罗模拟（一） 一元线性回归模拟

蒙特卡罗模拟因摩纳哥著名的赌场而得名。它能够帮助人们从数学上表述物理、化学、工程、经济学以及环境动力学中一些非常复杂的相互作用。

在线性回归模型中，我们通过理论学习，可以采用最小二乘法求解回归系数，然而，现实中总体回归方程总是未知的，我们如何知道样本是否较好的揭示了总体的特征呢？我们可以用蒙特卡罗模拟来验证线性回归的性质。

一、考虑如下数据生成过程或总体回归函数：

假设自变量和随机扰动项分别服从正态分布:

1. 当样本量不太大时，比如抽取30个样本,我们做回归：

clear //删除内存中已有数据
set obs 30  //确定抽取样本量为30
set seed 12345 //设定种子，方便重复验证
gen x = rnormal(4,9)   //得到服从正态分布均值为4，方差为9的随机数,作为x
gen u = rnormal(0,4)   //得到服从正态分布均值为0，方差为4的随机数,作为随机扰动u
gen y = 3 + 2*x + u    //按真实的总体回归函数计算y
reg y x   //做y对x的回归，检验回归结果与真实结果的差异

回归结果如下：

可以看出，当样本量为30的时候，回归系数为1.925，和我们真实回归系数2比较接近，常数项3.11和真实的3也比较接近，整体效果良好。

2. 为了验证大样本的性质，我们继续设置样本量为10000，再进行同样的操作（和上述代码相同，仅将set obs 30修改为 set obs 10000） 

clear //删除内存中已有数据
set obs 10000  //确定抽取样本量为30
set seed 12345 //设定种子，方便重复验证
gen x = rnormal(4,9)   //得到服从正态分布均值为4，方差为9的随机数,作为x
gen u = rnormal(0,4)   //得到服从正态分布均值为0，方差为4的随机数,作为随机扰动u
gen y = 3 + 2*x + u    //按真实的总体回归函数计算y
reg y x   //做y对x的回归，检验回归结果与真实结果的差异

回归结果：

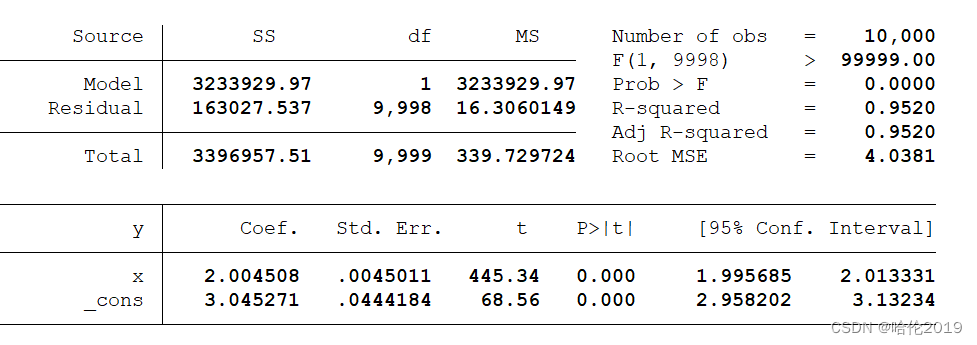
此时，我们发现回归系数2.0045，更加接近真实数据2，常数项3.04更接近真实数据3，验证了样本量越大，越接近真实结果的结论。 

二、图形展示回归结果

为了更好的比较真实值与回归模拟值，我们可作图：

twoway function PRF = 3 + 2*x,range(-3 13) || scatter y x || lfit y x,lpattern(dash)

结果如下：

这是10000个样本的 图，显得比较密集，如果做30个样本的图，则更清晰。