吴恩达|机器学习作业2.0Logistic 回归

2.0.Logistic 回归

1）题目：

在本部分的练习中，您将使用Logistic回归模型来预测一个学生是否被大学录取。假设你是大学某个院系的管理员，你想通过申请人在两门考试中的表现来决定每个人的录取率，你有来自以前申请人的历史数据，你可以用这些数据作为训练集建立Logistic回归，对每一个训练样本，你有申请人在两门考试中的分数和录取决定。
你的任务是建立一个分类模型，基于这两门课的分数来估计申请人的录取概率。
数据链接: https://pan.baidu.com/s/1-u0iDFDibZc6tTGGx9_wnQ 提取码: 351j

2）知识点概括：

• Logistic回归虽然名叫回归，但实际是一种分类算法。
  它的假设函数$h_{\theta }(x)=\frac{1}{1+e^{-{\theta }^{T}x}}$的估计值表示了输入值x的条件下得到y=1的概率，即该样例为正类的概率，即$h_{\theta }(x)=P(y=1|x;\theta )$
• ${\theta }^{T}x=0$称为决策边界（decision boundary）即对应了$h_{\theta }(x)=0.5$，它不是训练集的属性，而是假设本身及其参数的属性。若阈值为0.5，则$y=1$的区域为${\theta }^{T}x>0$，反之$y=0$的区域为${\theta }^{T}x<0$。
• 代价函数（cost function）为$J(\theta )=\frac{1}{m}{\sum }_{i=1}^{m}Cost(h_{\theta }(x^{(i)}),y^{(i)})=-\frac{1}{m}{\sum }_{i=1}^m[y^{(i)}log{h}_{\theta }(x^{(i)})+(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]$
• 梯度（gradient）为$\frac{\partial }{\partial {\theta }_j}J(\theta )=\frac{1}{m}{\sum }_{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$

3）大致步骤：

首先用pandas读取数据，数据处理好之后用.values转化为矩阵进行运算，然后可视化训练集数据，定义sigmoid函数、代价函数和梯度，带入更高级的算法中自动优化求解参数。
这里Ng推荐的算法有：共轭梯度法（conjugate gradient）、拟牛顿法（BFGS、L-BFGS）。
然后再进行对给定的某名学生的录取概率进行预测，并计算该分类器的精度、查准率和查全率。最后画出决策边界。

4）关于Python：

scipy中的optimize子包中提供了常用的最优化算法函数实现。我们可以直接调用这些函数完成我们的优化问题。具体可参考：

http://blog.sina.com.cn/s/blog_5f234d4701013ln6.html

本次练习主要采用了拟牛顿法、牛顿共轭梯度法和L-BFGS-B，其中需要输入目标函数、theta初始值、目标函数的梯度、最大迭代次数、传递给函数和梯度的值、并设置其他输出full_output=True（注意fmin_bfgs、fmin_ncg与fmin_l_bfgs_b参数不同，前两个需要选择full_output才可以返回优化的最小值，而fmin_l_bfgs_b默认返回）。

5）代码和结果：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt

data = pd.read_csv('ex2data1.txt', sep=',', names=['score1', 'score2', 'admission'])
(m, n) = data.shape
#截取并转化为矩阵
x = data[['score1', 'score2']]
x1 = pd.DataFrame(np.ones((m,1)), columns=['constant']) #在前面赋值一列1
x = pd.concat([x1, x], axis=1) #合并dataframe
y = data['admission'].astype(float) #y是int的需要转化为浮点型

x = x.values #从数据框转化为矩阵
y = y.values
theta = np.zeros(n) #赋值theta

'''可视化训练集数据'''
def plotData(data):
    positive = data[data.admission==1] #筛选出y=1的部分
    negative = data[data.admission==0]
    plt.scatter(positive.score1, positive.score2, c='k', marker='+', label='Admitted')
    plt.scatter(negative.score1, negative.score2, c='y', marker='o', label='Not Admitted')
    plt.legend(loc=1)
    plt.xlabel('Exam1 Score')
    plt.ylabel('Exam2 Score')
    
plt.figure(0)
plotData(data)

'''sigmoid函数'''
def sigmoid(x):
    return 1/(1+np.exp(-x))

'''计算代价函数和梯度'''
#代价函数
def cost_func(theta, x, y):
    m = y.size
    return -1/m*(y@np.log(sigmoid(x@theta))+(1-y)@np.log(1-sigmoid(x@theta)))

#梯度
def gradient_func(theta, x, y):
    m = y.size
    return 1/m*((sigmoid(x@theta))-y).T@x


'''求解最优参数'''
#方法一 BFGS
theta1, cost1, *unused1 = opt.fmin_bfgs(f=cost_func, fprime=gradient_func, x0=theta, args=(x, y), maxiter=400, full_output=True)

#方法二 牛顿共轭梯度
theta2, cost2, *unused2 = opt.fmin_ncg(f=cost_func, fprime=gradient_func, x0=theta, args=(x, y), maxiter=400, full_output=True)

#方法三 L-BFGS-B
theta3, cost3, *unused3 = opt.fmin_l_bfgs_b(func=cost_func, fprime=gradient_func, x0=theta, args=(x, y), maxiter=400)



'''预测与模型评价'''
#预测录取改率
def predict(x, theta):
    return sigmoid(x@theta)

x_test = [1, 45, 85]
print('The admission probabilities are %.4f  %.4f  %.4f respectively' %(predict(x_test, theta1),predict(x_test, theta2),predict(x_test, theta3)))

#阈值取0.5时的预测样例，即输出是正例还是反例
def p_or_n(theta, x=x):
    a = predict(x, theta)
    for i in range(a.size):
        if a[i]<0.5:
            a[i]=0
        else:
            a[i]=1
    return a

#精度
def accuracy(theta, x=x, y=y):
    m = y.size
    return 1-np.sum(np.abs(y-p_or_n(theta)))/m

#查准率
def precision(theta, x=x, y=y):
    p_p = pd.DataFrame((y+p_or_n(theta))) #转换成dataframe来计数，真正例预测也为正例
    return np.sum(p_p==2)/np.sum(p_or_n(theta)) #预测的正例中真实正例的比例

#查全率
def recall(theta, x=x, y=y):
    p_p = pd.DataFrame((y+p_or_n(theta))) #转换成dataframe来计数，真正例预测也为正例
    return np.sum(p_p==2)/np.sum(y) #真实正例中被预测为正例的比例

for i in range(1,4):
    print(accuracy(locals()['theta'+str(i)])) #变量名循环，依次打印精度
    
for i in range(1,4):
    print(precision(locals()['theta'+str(i)])) #变量名循环，依次打印查准率
    
for i in range(1,4):
    print(recall(locals()['theta'+str(i)])) #变量名循环，依次打印查全率


'''画出决策边界'''
#x@theta=0为决策边界，即theta[0]*1+theta[1]*x[1]+theta[2]*x[2]=0
def plotBD(theta,method,color):
    x1 = np.arange(25, 100, step=0.1)
    x2 = -(theta[0]+theta[1]*x1)/theta[2]
    plt.plot(x1, x2, label=method, c=color)
    plt.legend(loc=3)
    plt.title('The Decision Boundary')

plt.figure(1)
plotData(data)
plotBD(theta1,'BFGS','g')
plotBD(theta2,'NCG','r')
plotBD(theta3,'L-BFGS-B','b')
plt.show

BFGS、牛顿共轭梯度、L-BFGS-B的迭代次数分别为23、26和27。
三种方法所求的最优参数和最后的代价函数值分别为

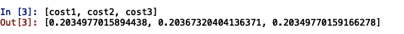
三种方法预测的成绩分别为45、85的学生的录取概率为（期望值为0.776）

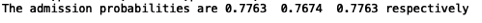
虽然从代价函数和单个学生的录取概率准确性来说，第二种方法即牛顿共轭梯度不如拟牛顿表现好，但是当阈值取0.5时，三种方法的精度（0.89）、查准率（0.901639）、查全率（0.916667）完全相同，且仔细查看后发现他们虽然对每个训练集的预测录取概率有所差别，但是在阈值0.5下所产生的预测正反例完全一样。

三种方法预测的正反例矩阵一样：

自然三种方法的决策边界也一样：