矩阵分解模型——SVD与SVD++

推荐的框架可简单的理解为：

在召回过程中，模型一般使用协同过滤或者深度模型等。协同过滤的方法大致可分为两大类，一类为基于领域的方法，例如User-based CF、Item-based CF，第二类为基于模型的方法，即隐语义模型，矩阵分解模型是实现隐语义模型（Latent Factor Model，LFM）使用最广泛的一种方法。

在数学上SVD可以对一个稠密的矩阵进行分解，分解为三个矩阵相乘，选择合适的维数对原始矩阵进行重构，可以达到降维的目的。Funk-SVD分解为两个矩阵，一个和用户相关，一个和物品相关，而且还使用了L2正则化，这样可以适用于稀疏矩阵，计算复杂度低，还能防止过拟合。在Funk-SVD上，加入了各项的偏置项，引出了Bias-SVD。在此基础上，再加入用户反馈的考量，修改模型就得到了SVD++算法。

其实我个人认为Funk-SVD、Bias-SVD和SVD++与数学上的SVD并没有特别本质的联系，只是都是矩阵分解的技术，对数学不感兴趣可以直接从Funk-SVD开始看。后面三个算法层层递进，一步步变得更复杂也更完善，效果也更佳。

一、SVD原理

矩阵的一些定义：

1. 正交矩阵：$A{A}^T=I_n$
2. 正定矩阵：对任意非零实向量$x$，有$xA{x}^T>0$，则$A$为正定矩阵，若$xA{x}^T\ge 0$则$A$为半正定矩阵
3. 酉矩阵：$U^{H}U=U{U}^H=I_n$，其中${}^H$表示共轭转置，则$U$为酉矩阵
4. 正规矩阵：$U^{H}U=U{U}^H$，其中${}^H$表示共轭转置，则$U$为正规矩阵

从上面的定义可以看出：

1. 当正规矩阵$U$满足$U^{H}U=U{U}^H=I_n$时，则$U$为酉矩阵；
2. 当酉矩阵$U$为实矩阵时，则$U$是正交矩阵（因为此时的共轭转置等价于转置）
   注：实际上我们应用中处理到的数据都是实数，所以嫌太麻烦下面可以将酉矩阵忽略直接理解为正交矩阵就行

在高代中有谱定理：

若矩阵$M$是一个正规矩阵，则存在酉矩阵$U$，以及对角矩阵$\Sigma$，使得：$$M=U\Sigma U^T$$即正规矩阵可以经过酉变换分解为对角矩阵。

但谱定理中要求的正规矩阵很严格，一般矩阵都不满足这个条件，SVD分解是比较宽松的一种矩阵分解技术。

奇异值分解（Singular Value Decomposition，简称SVD）：

若矩阵$M$是一个$m\times n$的矩阵，其中所有元素全部属于实数域或者复数域，则存在$m\times m$的酉矩阵$U$，半正定的$m\times n$的对角矩阵$\Sigma$，以及$n\times n$的酉矩阵$V$，使得：$$M_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^H$$一般将$\Sigma$中的对角线元素从大到小排列，此时$\Sigma$由$M$唯一确定。

对于SVD的计算：
因为：
$$\begin{array}{rl}M{M}^H& =U\Sigma V^{H}V{\Sigma }^H{U}^H=U(\Sigma {\Sigma }^H)U^H\\ M^{H}M& =V{\Sigma }^H{U}^{H}U\Sigma V^H=V({\Sigma }^H\Sigma )V^H\end{array}$$

所以$U$的列向量是$M{M}^H$的特征向量，$V$的列向量是$M^{H}M$的特征向量，$M$的奇异值是$M{M}^H$或$M^{H}M$的非零的平方根。

按照这个结果，可以先分别计算出$M{M}^H$和$M^{H}M$的特征值和特征向量，具体计算方式是用行列式为零来求（略），注意特征向量并不唯一，这样得到的特征值按照从大到小排列起来的对角矩阵组成了$\Sigma$的对角线部分，对应的特征向量分别组成$U$和$V$，就得到了SVD分解。（下面是我手算的一个过程，比较潦草，也可忽略）

有了SVD分解之后，即$$M_{m\times n}=U_{m\times m}{\Sigma }_{m\times n}{V}_{n\times n}^H$$可以选择部分较大的一些奇异值来进行降维，因为奇异值的大小代表了信息含量的多少，舍弃掉一些奇异值小的部分相当于剔除掉某些噪音或者不太重要的信息。

假设维数降至$k(k<min(n,m))$，则原本的矩阵$M$可以这样近似：$$M_{m\times n}\approx U_{m\times k}{\Sigma }_{k\times k}{V}_{k\times n}^H$$

例如：上面手算的矩阵所有特征值全选取的话忽略计算中的近似位数截取带来的误差，基本上能正确还原：

假设降维为$k=1$（reshape是因为Python中一维数组自动展开，矩阵相乘时会影响，加上保证矩阵相乘正确，若维数比较高的话不用加reshape的），即:

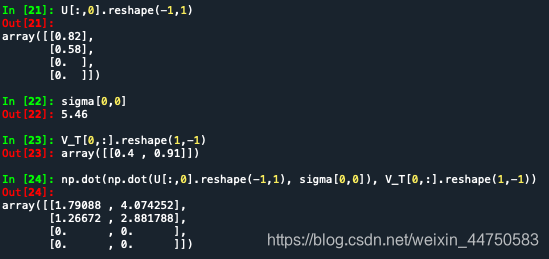
也可以在一定程度上近似还原出矩阵$M$。

所以，分解后若要根据分解的矩阵来计算原始评分矩阵$M$中的第$i$行第$j$列元素$m_{ij}$，可以直接取$U_{m\times k}$的第$i$行向量，即$u_i$，以及$V_{k\times n}^H$的第$j$列向量，即$v_j$，则$m_{ij}=u_i^T{\Sigma }_{k\times k}{v}_j$。这个基本上就是SVD矩阵分解的原理。

但SVD在实际的推荐应用中较少用到，肯定是有缺陷存在的：一是因为SVD分解要求矩阵稠密，而推荐中的评分矩阵大多数都是稀疏，例如在电影评分矩阵中，绝大多数用户看过的电影肯定是较少的，导致矩阵中大多数数据都是缺失，若要使用SVD就必须手动补齐评分矩阵，一般可以用均值补齐，但这样一来评分矩阵可能会失真；此外，SVD分解的时间复杂度为$O(n^3)$，对于这样补齐后的稠密矩阵来说，如果矩阵较小那计算代价还能接受，但在推荐的海量数据下评分矩阵很大，使用SVD分解计算代价太大。

二、Funk-SVD

1、原理

SVD是将评分矩阵分解成3个矩阵来达到降维的目的，Funk-SVD则是分解成2个矩阵，一个用户相关的矩阵$P_{m\times k}$，一个物品相关的矩阵$Q_{n\times k}$，由此来对原始评分矩阵$M$进行重构，即$$M_{m\times n}=P_{m\times k}{Q}_{k\times n}^T$$

重构的方法就是采用线性回归的思想，定义一个MSE loss，使用梯度下降法来逐步的最小化真实评分$m_{ui}$和预测评分$q_i^T{p}_u$之间的平方损失，使得已经有打分的真实评分和预测评分尽可能接近，即$$\min MSE(M_{m\times n}-P_{m\times k}{Q}_{k\times n}^T)=\min \sum _{(u,i)\in R}(m_{ui}-q_i^T{p}_u{)}^2$$

其中$(u,i)\in R$表示所有有评分的那些位置，这样相当于把没有评分的位置权重设置为0，有评分的设置为1，就可以直接对稀疏的评分矩阵进行分解，不需要像上面SVD那样先变成稠密矩阵再分解，减少了计算量。而且学习到$P,Q$矩阵之后就可以对未打分的那些位置也进行预测打分了。

所以在这里，矩阵$P,Q$的每个元素都是要学习的参数。为了防止过拟合，Funk-SVD还加入了L2正则化，对参数进行惩罚，所以损失函数变为：$$\ell =\sum _{(u,i)\in R}(m_{ui}-q_i^T{p}_u{)}^2+\lambda (\Vert q_i{\Vert }^2+\Vert p_u{\Vert }^2)$$

模型的解释：
这里的$k$是事先设定的降维后的维数，一般是远小于评分矩阵的维数$m,n$的。从embedding的思想来看，Funk-SVD可以解释为对每一个用户和每一个物品分别求他们的embedding向量，即$p_u$为user embedding，$q_i$为item embedding，其实本质就是把用户和物品都映射到一个较低的$k$维空间中，这$k$维向量在物品身上表现为属性特征，在用户身上表现为偏好特征，我们认为用户对物品的评分主要是受这些隐向量影响，只不过和word embedding一样，这些隐向量并不具有实际意义，也不一定具有非常好的可解释性，每一个维度也没有确定的标签名字。

在这个损失函数的基础上，对模型进行训练和优化可直接采用梯度下降法，对参数$p_u,q_i$求导，得到：
$$\begin{gathered} \frac{\partial \ell }{\partial p_u}=-2(m_{ui}-q_i^T{p}_u)q_i+2\lambda p_u \\ \frac{\partial \ell }{\partial q_i}=-2(m_{ui}-q_i^T{p}_u)p_u+2\lambda q_i \end{gathered}$$

若记$m_{ui}-q_i^T{p}_u=e_{ui}$，学习率为$\gamma$，则参数的更新公式为：
$$\begin{gathered} p_u=p_u+\gamma (e_{ui}{q}_i-\lambda p_u) \\ {q}_i=q_i+\gamma (e_{ui}{p}_u-\lambda q_i) \end{gathered}$$

学习到$P,Q$矩阵之后就可以对未打分的那些位置也进行预测打分了。

2、代码实现

数据集使用的是ml-100k。
关于优化算法，代码里采用的是SGD，后续可以进一步改成mini-batch GD等。
我把其中u.data这个文件改成data.txt，放在百度云上可以直接取用，提取码: ja5t

import numpy as np
import pandas as pd

# 用DataFrame来储存数据，格式为userid, itemid, rating
df = pd.read_csv('data.txt', sep='\t', header=None)
df.drop(3, inplace=True, axis=1) # 去掉时间戳
df.columns = ['uid', 'iid', 'rating']

# 随机打乱划分训练和测试集
df = df.sample(frac=1, random_state=0)
train_set = df.iloc[:int(len(df)*0.75)]
test_set = df.iloc[int(len(df)*0.75):]

n_users = max(df.uid)+1 # +1是因为uid最小是从1开始，懒得在pu切片中-1，所以多一维空着也没事
n_items = max(df.iid)+1

class Funk_SVD(object):
    def __init__(self, n_epochs, n_users, n_items, n_factors, lr, reg_rate, random_seed=0):
        self.n_epochs = n_epochs
        self.lr = lr
        self.reg_rate = reg_rate
        np.random.seed(random_seed)
        self.pu = np.random.randn(n_users, n_factors) / np.sqrt(n_factors) # 参数初始化不能太大
        self.qi = np.random.randn(n_items, n_factors) / np.sqrt(n_factors)
        
    def predict(self, u, i):
        return np.dot(self.qi[i], self.pu[u])
        
    def fit(self, train_set, verbose=True):
        for epoch in range(self.n_epochs):
            mse = 0
            for index, row in train_set.iterrows():
                u, i, r = row.uid, row.iid, row.rating
                error = r - self.predict(u, i)
                mse += error**2
                tmp = self.pu[u]
                self.pu[u] += self.lr * (error * self.qi[i] - self.reg_rate * self.pu[u])
                self.qi[i] += self.lr * (error * tmp - self.reg_rate * self.qi[i])
            if verbose == True:
                rmse = np.sqrt(mse / len(train_set))
                print('epoch: %d, rmse: %.4f' % (epoch, rmse))
        return self
    
    def test(self, test_set):
        predictions = test_set.apply(lambda x: self.predict(x.uid, x.iid), axis=1)
        rmse = np.sqrt(np.sum((test_set.rating - predictions)**2) / len(test_set))
        return rmse
    
funk_svd = Funk_SVD(n_epochs=20, n_users=n_users, n_items=n_items, n_factors=35, lr=0.005, reg_rate=0.02)
funk_svd.fit(train_set, verbose=True)
funk_svd.test(test_set)
# 0.9872467462373891
funk_svd.predict(120, 282) 
# 测试集中的某一条数据，真实评分为4，预测为3.233268069895416

训练的过程是比较慢的，之前我试了下surprise库中的SVD，这个算法的实现其实就是bias-SVD，如果把bias设置为biased=False，用surprise自带的ml-100k来做的话最后测试集的rmse能到0.9466左右，而且速度快很多。效果的原因可能是和参数的初始化有关，速度影响可能和数据结构有关。

三、Bias-SVD

1、原理

Bias-SVD其实很简单，就是对上述Funk-SVD加入偏置项的改进。即把预测评分从之前简单的$q_i^T{p}_u$定义为：$${\hat{m}}_{ui}=\mu +b_u+b_i+q_i^T{p}_u$$

其中$\mu$是global bias，表示训练数据的总体评分情况，一般可以设置为这个训练数据中所有打分的均值，为常数。因为有的训练集可能整体的评分偏高，而有的整体偏低，这种整体性无关个别用户或者物品。

其中$b_u$为用户的偏差，是一个需要训练的参数，表示某一特定用户的打分习惯。因为对于同一批物品，可能某个用户是批判性较强的，他整体给这批物品打分就是比那种乐观的用户低，即使他们给了同一个物品同样的分数，这两个分数之间代表的喜好程度显然不一样。

类似的，$b_i$为物品的偏差，也是需要训练的参数，表示某一特定物品得到的打分情况。因为有的质量较高的物品评分普遍比质量低的评分高，这种偏差和用户的喜好程度无关，因此加一些这种偏差在模型中十分合理，且效果很好。

对应的，损失函数也要对偏差进行惩罚，所以最终Bias-SVD的损失函数变为：$$\ell =\sum _{(u,i)\in R}(m_{ui}-\mu -b_u-b_i-q_i^T{p}_u{)}^2+\lambda (b_u^2+b_i^2+\Vert q_i{\Vert }^2+\Vert p_u{\Vert }^2)$$

类似的，记$m_{ui}-\mu -b_u-b_i-q_i^T{p}_u=e_{ui}$，在这个损失函数的基础上，采用梯度下降法，对参数$b_u,b_i,p_u,q_i$求导，得到：
$$\begin{gathered} \frac{\partial \ell }{\partial b_u}=-2e_{ui}+2\lambda b_u \\ \frac{\partial \ell }{\partial b_i}=-2e_{ui}+2\lambda b_i \\ \frac{\partial \ell }{\partial p_u}=-2e_{ui}{q}_i+2\lambda p_u \\ \frac{\partial \ell }{\partial q_i}=-2e_{ui}{p}_u+2\lambda q_i \end{gathered}$$

若记学习率为$\gamma$，则参数的更新公式为：
$$\begin{gathered} b_u=b_u+\gamma (e_{ui}-\lambda b_u) \\ {b}_i=b_i+\gamma (e_{ui}-\lambda b_i) \\ {p}_u=p_u+\gamma (e_{ui}{q}_i-\lambda p_u) \\ {q}_i=q_i+\gamma (e_{ui}{p}_u-\lambda q_i) \end{gathered}$$

学习到$P,Q$矩阵之后就可以对未打分的那些位置也进行预测打分了。

2、代码实现

在Funk_SVD基础上添一点改一点就OK

class Bias_SVD(object):
    def __init__(self, n_epochs, n_users, n_items, n_factors, lr, reg_rate, random_seed=0):
        self.n_epochs = n_epochs
        self.lr = lr
        self.reg_rate = reg_rate
        np.random.seed(random_seed)
        self.pu = np.random.randn(n_users, n_factors) / np.sqrt(n_factors)
        self.qi = np.random.randn(n_items, n_factors) / np.sqrt(n_factors)
        self.bu = np.zeros(n_users, np.double)
        self.bi = np.zeros(n_items, np.double)
        self.global_bias = 0
        
    def predict(self, u, i):
        return self.global_bias + self.bu[u] + self.bi[i] + np.dot(self.qi[i], self.pu[u])
        
    def fit(self, train_set, verbose=True):
        self.global_bias = np.mean(train_set.rating)
        for epoch in range(self.n_epochs):
            mse = 0
            for index, row in train_set.iterrows():
                u, i, r = row.uid, row.iid, row.rating
                error = r - self.predict(u, i)
                mse += error**2
                self.bu[u] += self.lr * (error - self.reg_rate * self.bu[u])
                self.bi[i] += self.lr * (error - self.reg_rate * self.bi[i])
                tmp = self.pu[u]
                self.pu[u] += self.lr * (error * self.qi[i] - self.reg_rate * self.pu[u])
                self.qi[i] += self.lr * (error * tmp - self.reg_rate * self.qi[i])
            if verbose == True:
                rmse = np.sqrt(mse / len(train_set))
                print('epoch: %d, rmse: %.4f' % (epoch, rmse))
        return self
    
    def test(self, test_set):
        predictions = test_set.apply(lambda x: self.predict(x.uid, x.iid), axis=1)
        rmse = np.sqrt(np.sum((test_set.rating - predictions)**2) / len(test_set))
        return rmse

bias_svd = Bias_SVD(n_epochs=20, n_users=n_users, n_items=n_items, n_factors=35, lr=0.005, reg_rate=0.02)
bias_svd.fit(train_set, verbose=True)
bias_svd.test(test_set)
# 0.9642304425644652
bias_svd.predict(120, 282) 
# 真实评分为4，预测为3.495711940570076

四、SVD++

1、原理

上述两种改进的SVD都是利用两个向量进行学习，即用户embedding和物品embedding，分别表示用户的属性信息和物品的属性信息。在这个基础上，SVD++引入了一个隐式反馈向量$y_j$，它表示用户有过行为的物品集合的一个embedding向量。

本质上来说，$y_j$这个embedding向量其实还是物品的embedding，而且维度也是和$p_u,q_i$是一样的，都是$k$维的，但不同的是它表示用户操作过的物品的特性。将这些用户操作过的物品embedding向量加起来且归一化后，用来表达用户的兴趣偏好，这样多了一些额外的信息。所以SVD++的预测打分变为：$${\hat{m}}_{ui}=\mu +b_u+b_i+q_i^T(p_u+|I_u{|}^{-1/2}\sum _{j\in I_u}{y}_j)$$

其中$p_u$表示用户的属性信息，$|I_u{|}^{-1/2}{\sum }_{j\in I_u}{y}_j$则表示基于这些物品用户的偏好信息，$I_u$表示用户操作过的物品集合，例如用户评过分的那些电影集，或用户浏览过的物品集，$|I_u{|}^{-1/2}$为归一化系数，消除由集合个数差异带来的影响。

因此，SVD++的损失函数变为：$$\begin{gathered} \ell =\sum _{(u,i)\in R}\left(\right(m_{ui}-\mu -b_u-b_i-q_i^T(p_u+|I_u{|}^{-1/2}\sum _{j\in I_u}{y}_j){)}^2 \\ +\lambda (b_u^2+b_i^2+\Vert q_i{\Vert }^2+\Vert p_u{\Vert }^2+\sum _{j\in I_u}\Vert y_j{\Vert }^2\left)\right) \end{gathered}$$

类似的，记$m_{ui}-\mu -b_u-b_i-q_i^T(p_u+|I_u{|}^{-1/2}{\sum }_{j\in I_u}{y}_j)=e_{ui}$，在这个损失函数的基础上，采用梯度下降法，对参数$b_u,b_i,p_u,q_i,y_j$求导，得到：
$$\begin{gathered} \frac{\partial \ell }{\partial b_u}=-2e_{ui}+2\lambda b_u \\ \frac{\partial \ell }{\partial b_i}=-2e_{ui}+2\lambda b_i \\ \frac{\partial \ell }{\partial p_u}=-2e_{ui}{q}_i+2\lambda p_u \\ \frac{\partial \ell }{\partial q_i}=-2e_{ui}(p_u+|I_u{|}^{-1/2}\sum _{j\in I_u}{y}_j)+2\lambda q_i \\ \frac{\partial \ell }{\partial y_j}=-2e_{ui}\cdot |I_u{|}^{-1/2}\cdot q_i+2\lambda y_j \end{gathered}$$

若记学习率为$\gamma$，则参数的更新公式为：
$$\begin{gathered} b_u=b_u+\gamma (e_{ui}-\lambda b_u) \\ {b}_i=b_i+\gamma (e_{ui}-\lambda b_i) \\ {p}_u=p_u+\gamma (e_{ui}{q}_i-\lambda p_u) \\ {q}_i=q_i+\gamma (e_{ui}(p_u+|I_u{|}^{-1/2}\sum _{j\in I_u}{y}_j)-\lambda q_i) \\ {y}_j=y_j+\gamma (e_{ui}\cdot |I_u{|}^{-1/2}\cdot q_i-\lambda y_j) \end{gathered}$$

2、代码实现

加入了用户反馈之后的运行速度明显慢了许多。

class SVDpp(object):
    def __init__(self, n_epochs, n_users, n_items, n_factors, lr, reg_rate, random_seed=0):
        self.n_epochs = n_epochs
        self.lr = lr
        self.reg_rate = reg_rate
        self.n_factors = n_factors
        np.random.seed(random_seed)
        self.pu = np.random.randn(n_users, n_factors) / np.sqrt(n_factors)
        self.qi = np.random.randn(n_items, n_factors) / np.sqrt(n_factors)
        self.yj = np.random.randn(n_items, n_factors) / np.sqrt(n_factors)
        self.bu = np.zeros(n_users, np.double)
        self.bi = np.zeros(n_items, np.double)
        self.global_bias = 0
        self.Iu = dict()
        
    def reg_sum_yj(self, u, i):
        sum_yj = np.zeros(self.n_factors, np.double)
        for j in self.Iu[u]:
            sum_yj += self.yj[j]
        return sum_yj / np.sqrt(len(self.Iu[u]))
        
    def predict(self, u, i, feedback_vec_reg):
        return self.global_bias + self.bu[u] + self.bi[i] + np.dot(self.qi[i], self.pu[u] + feedback_vec_reg)
        
    def fit(self, train_set, verbose=True):
        self.global_bias = np.mean(train_set.rating)
        # 将用户打过分的记录到Iu字典中，key为uid，value为打过分的iid的list
        g = train_set.groupby(['uid'])
        for uid, df_uid in g:
            self.Iu[uid] = list(df_uid.iid)
        
        for epoch in range(self.n_epochs):
            square_err = 0
            for index, row in train_set.iterrows():
                u, i, r = row.uid, row.iid, row.rating
                feedback_vec_reg = self.reg_sum_yj(u, i)
                error = r - self.predict(u, i, feedback_vec_reg)
                square_err += error**2
                self.bu[u] += self.lr * (error - self.reg_rate * self.bu[u])
                self.bi[i] += self.lr * (error - self.reg_rate * self.bi[i])
                tmp_pu = self.pu[u]
                tmp_qi = self.qi[i]
                self.pu[u] += self.lr * (error * self.qi[i] - self.reg_rate * self.pu[u])
                self.qi[i] += self.lr * (error * (tmp_pu + feedback_vec_reg) - self.reg_rate * self.qi[i])
                for j in self.Iu[u]:
                    self.yj[j] += self.lr * (error / np.sqrt(len(self.Iu[u])) * tmp_qi - self.reg_rate * self.yj[j])
            if verbose == True:
                rmse = np.sqrt(square_err / len(train_set))
                print('epoch: %d, rmse: %.4f' % (epoch, rmse))
        return self
    
    def test(self, test_set):
        predictions = test_set.apply(lambda x: self.predict(x.uid, x.iid, self.reg_sum_yj(x.uid, x.iid)), axis=1)
        rmse = np.sqrt(np.sum((test_set.rating - predictions)**2) / len(test_set))
        return rmse

svdpp = SVDpp(n_epochs=20, n_users=n_users, n_items=n_items, n_factors=35, lr=0.005, reg_rate=0.02)
svdpp.fit(train_set, verbose=True)
svdpp.test(test_set)
# 0.9510302683304096
svdpp.predict(120, 282, svdpp.reg_sum_yj(120, 282)) 
# 真实评分为4，预测为3.5370712737668204

参考资料

1. 矩阵分解之SVD奇异值分解
2. 矩阵分解在协同过滤推荐算法中的应用-刘建平Pinard
3. 推荐算法之矩阵分解
4. surprise文档——Matrix Factorization-based algorithms