2.1.正则化的Logistic 回归
1)题目:
在本部分的练习中,您将使用正则化的Logistic回归模型来预测一个制造工厂的微芯片是否通过质量保证(QA),在QA过程中,每个芯片都会经过各种测试来保证它可以正常运行。假设你是这个工厂的产品经理,你拥有一些芯片在两个不同测试下的测试结果,从这两个测试,你希望确定这些芯片是被接受还是拒绝,为了帮助你做这个决定,你有一些以前芯片的测试结果数据集,从中你可以建一个Logistic回归模型。
数据链接: https://pan.baidu.com/s/1-u0iDFDibZc6tTGGx9_wnQ 提取码: 351j
2)知识点概括:
-
欠拟合:underfitting / high bias
-
过拟合:overfitting / high variance 一般在多个特征中,训练集拟合得非常好,代价函数可能接近于0,但是泛化能力差,对于预测新样本效果不佳
-
解决方法:
1)减少特征数量
手动选择特征
模型选择算法(model selection algorithm)
2)正则化(regularization)
保留所有特征,但是减小参数的量级或者取值(加入正则化项/惩罚项) -
线性回归的正则化
1)正则化过程:
得到正则化代价函数 J ( θ ) = 1 2 m [ ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) 2 + λ ∑ j = 1 n θ j 2 ] J(\theta)={1\over {2m}}[\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2}+\lambda\sum_{j=1}^n\theta_j^2] J(θ)=2m1[∑i=1m(hθ(x(i))−y(i))2+λ∑j=1nθj2](注意 θ 0 \theta_0 θ0不加入惩罚)
λ \lambda λ称正则化参数(regularization parameter), λ \lambda λ过大会导致假设模型偏见性太强,即欠拟合,使得每个参数接近0,代价函数变成一条水平线。
2)梯度下降法:
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_0:=\theta_0-\alpha {1\over m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
θ j : = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] = θ j ( 1 − α λ m ) − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\alpha [{1\over m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+{\lambda\over m}\theta_j]= \theta_j(1-\alpha{\lambda\over m})-\alpha {1\over m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−α[m1∑i=1m(hθ(x(i))−y(i))xj(i)+mλθj]=θj(1−αmλ)−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
( j = 1 , 2 , 3 , ⋯   , n ) (j=1,2,3,\cdots,n) (j=1,2,3,⋯,n)
其中 ( 1 − α λ m ) (1-\alpha{\lambda\over m}) (1−αmλ)略小于1使得参数在每次迭代中逐渐缩小
3)正规方程法:
θ = ( X T X + λ A ) − 1 X T y \theta=(X^TX+\lambda A)^{-1}X^Ty θ=(XTX+λA)−1XTy
其中 X X X的维数为 X m × ( n + 1 ) X_{m\times(n+1)} Xm×(n+1) , y y y的维数为 y m × 1 y_{m\times 1} ym×1
矩阵 A A A是一个 ( n + 1 ) × ( n + 1 ) (n+1)\times(n+1) (n+1)×(n+1)阶对角元素分别为 0 , 1 , 1 , ⋯   , 1 0,1,1,\cdots,1 0,1,1,⋯,1的对角阵
若 m ≤ n m\le n m≤n,矩阵 X T X X^TX XTX是一个不可逆/奇异/退化矩阵,用伪逆矩阵求得也不会有很好的模型,但正则化之后大括号里的矩阵一定可逆。 -
正则化逻辑回归:
代价函数:
J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g h θ ( x ( i ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] + λ 2 m ∑ j = 1 n θ j 2 J(\theta)=-{1\over m}\sum_{i=1}^m[y^{(i)}logh_\theta(x^{(i)})+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] +{\lambda\over 2m}\sum_{j=1}^n\theta_j^2 J(θ)=−m1∑i=1m[y(i)loghθ(x(i))+(1−y(i))log(1−hθ(x(i)))]+2mλ∑j=1nθj2
梯度:
θ 0 : = θ 0 − α 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_0:=\theta_0-\alpha {1\over m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θ0:=θ0−αm1∑i=1m(hθ(x(i))−y(i))xj(i)
θ j : = θ j − α [ 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) + λ m θ j ] \theta_j:=\theta_j-\alpha [{1\over m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}+{\lambda\over m}\theta_j] θj:=θj−α[m1∑i=1m(hθ(x(i))−y(i))xj(i)+mλθj]
( j = 1 , 2 , 3 , ⋯   , n ) (j=1,2,3,\cdots,n) (j=1,2,3,⋯,n)
只需自己定义代价函数、梯度函数(每个参数的偏导数),然后调用其他高级算法的函数即可求解出参数。scipy中的optimize子包中提供了常用的最优化算法函数实现。
2)大致步骤:
首先用pandas读取数据,数据处理好之后用.values转化为矩阵进行运算,然后可视化训练集数据。从散点图中可以看出正反例并没有线性决策边界,因此需要进行特征映射(feature mapping)创建更多的特征,即高阶项,使得决策边界为高阶函数的形状而非线性。
这里希望每个特征增加高阶项直到六阶,也就是会产生28维的特征矩阵。
然后再计算代价函数和梯度,注意这里均不惩罚theta的第一项。再和作业2.0一样利用高级的算法中自动优化求解参数。然后再进行对给定的某名学生的录取概率进行预测,并计算该分类器的精度、查准率和查全率。最后画出决策边界。
3)关于Python:
画决策边界时使用plt.contour,这是用来绘制等高线图形的。
.iat[i, j]用来返回dataframe格式的第i行第j列元素。
dataframe转化成array:df=df.values
array转化成dataframe:df = pd.DataFrame(df)
本次练习在最后画决策边界时用到了特征映射的函数,但之前定义时是在dataframe下定义的,后来运算都是采用array,导致引用函数时格式不对,转换之后运行内存需要很大,以后要注意在写函数的时候考虑到之后的数据格式,以免发生类似的错误!
4)代码和结果:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import scipy.optimize as opt
from mapFeature import *
data = pd.read_csv('ex2data2.txt', names=['test1', 'test2', 'accepted'])
(m, n) = data.shape
'''可视化训练集数据'''
def plotData(data):
positive = data[data.accepted==1] #筛选出y=1的部分
negative = data[data.accepted==0]
plt.scatter(positive.test1, positive.test2, c='k', marker='+', label='Accepted')
plt.scatter(negative.test1, negative.test2, c='y', marker='o', label='Rejected')
plt.legend(loc=1)
plt.xlabel('Microchip test1')
plt.ylabel('Microchip test2')
plt.figure(0)
plotData(data)
'''特征映射,创建高阶项特征'''
#截取并转化为矩阵
x1 = data['test1']
x2 = data['test2']
x = mapFeature(x1, x2, 6) #这里的x已经是28维的了
y = data['accepted']
x = x.values #从数据框转化为矩阵
y = y.values
theta = np.zeros(x.shape[1]) #赋值theta
'''sigmoid函数'''
def sigmoid(x):
return 1/(1+np.exp(-x))
'''计算代价函数和梯度'''
#原本代价函数
def cost_func(theta, x, y):
m = y.size
return -1/m*(y@np.log(sigmoid(x@theta))+(1-y)@np.log(1-sigmoid(x@theta)))
#正则化的代价函数,不惩罚第一项theta[0]
def cost_reg(theta, x, y, l=1):
m = y.size
theta_ = theta[1:] #选取第二项以后的
return cost_func(theta, x, y) + l/(2*m)*np.sum(theta_*theta_)
#原本的梯度
def gradient_func(theta, x, y):
m = y.size
return 1/m*((sigmoid(x@theta))-y).T@x
#正则化的的梯度,不惩罚第一项theta[0]
def gradient_reg(theta, x, y, l=1):
theta_ = l/(y.size)*theta
theta_[0] = 0 #第一项不惩罚设为0
return gradient_func(theta, x, y) + theta_
'''求解最优参数'''
#方法一 BFGS
theta1, cost1, *unused1 = opt.fmin_bfgs(f=cost_reg, fprime=gradient_reg, x0=theta, args=(x, y), maxiter=400, full_output=True)
#方法二 牛顿共轭梯度
theta2, cost2, *unused2 = opt.fmin_ncg(f=cost_reg, fprime=gradient_reg, x0=theta, args=(x, y), maxiter=400, full_output=True)
#方法三 L-BFGS-B
theta3, cost3, *unused3 = opt.fmin_l_bfgs_b(func=cost_reg, fprime=gradient_reg, x0=theta, args=(x, y), maxiter=400)
'''预测与模型评价'''
#预测录取改率
def predict(x, theta):
return sigmoid(x@theta)
#阈值取0.5时的预测样例,即输出是正例还是反例
def p_or_n(theta, x=x):
a = predict(x, theta)
for i in range(a.size):
if a[i]<0.5:
a[i]=0
else:
a[i]=1
return a
#精度
def accuracy(theta, x=x, y=y):
m = y.size
return 1-np.sum(np.abs(y-p_or_n(theta)))/m
#查准率
def precision(theta, x=x, y=y):
p_p = pd.DataFrame((y+p_or_n(theta))) #转换成dataframe来计数,真正例预测也为正例
return np.sum(p_p==2)/np.sum(p_or_n(theta)) #预测的正例中真实正例的比例
#查全率
def recall(theta, x=x, y=y):
p_p = pd.DataFrame((y+p_or_n(theta))) #转换成dataframe来计数,真正例预测也为正例
return np.sum(p_p==2)/np.sum(y) #真实正例中被预测为正例的比例
for i in range(1,4):
print(accuracy(locals()['theta'+str(i)])) #变量名循环,依次打印精度
for i in range(1,4):
print(precision(locals()['theta'+str(i)])) #变量名循环,依次打印查准率
for i in range(1,4):
print(recall(locals()['theta'+str(i)])) #变量名循环,依次打印查全率
'''画出决策边界'''
#x@theta=0为决策边界,这里懒得重新写一个特征映射函数,后来还是觉得重新写函数比较方便些
plt.figure(1)
plotData(data)
u = np.linspace(-1, 1.5, 100)
v = np.linspace(-0.8, 1.2, 100)
z = np.zeros((u.size,v.size)) #将原始数据变成网格数据形式,也可以用np.meshgrid
for i in range(0, u.size):
for j in range(0, v.size):
z[i, j] = np.array([1, u[i],v[j], u[i]**2,u[i]*v[j],v[j]**2, u[i]**3,u[i]*u[i]*v[j],u[i]*v[j]**2,v[j]**3, u[i]**4,(u[i]**3)*v[j],u[i]*u[i]*v[j]**2,u[i]*v[j]**3,v[j]**4, u[i]**5,(u[i]**4)*v[j],(u[i]**3)*v[j]**2,u[i]*u[i]*v[j]**3,u[i]*v[j]**4,v[j]**5, u[i]**6,(u[i]**5)*v[j],(u[i]**4)*v[j]**2,u[i]*u[i]*u[i]*v[j]**3,u[i]*u[i]*v[j]**4,u[i]*v[j]**5,v[j]**6])@theta3
C = plt.contour(u, v, z, 0, colors='b', label='Decision Boundary')
plt.legend()
plt.title('The Decision Boundary')
plt.show
#虽然代码看起来比较简单,但是运行内存太大,速度特别慢,以后需要注意
plt.figure(1)
plotData(data)
u = np.linspace(-1, 1.5, 100)
v = np.linspace(-0.8, 1.2, 100)
z = np.zeros((u.size,v.size)) #将原始数据变成网格数据形式,也可以用np.meshgrid
for i in range(0, u.size):
for j in range(0, v.size):
change = mapFeature(pd.DataFrame([u[i]]), pd.DataFrame([v[j]]), 6)
z[i, j] = (change.values)@theta2
C = plt.contour(u, v, z, 0, colors='b', label='Decision Boundary')
plt.legend()
plt.title('The Decision Boundary')
plt.show
import pandas as pd
import numpy as np
def mapFeature(x, y, power):
result = pd.DataFrame(np.ones((x.size,1)), columns=['00']) #在前面赋值一列1
for i in range(1, power+1):
for j in range(i+1):
z = x**(i-j)*y**j
result = pd.concat([result, z], axis=1) #合并dataframe
return result
当
λ
=
1
\lambda=1
λ=1时,三种方法的迭代次数分别为47、6、16,下图可以看出三种方法的精度、查准率和查全率均一样,分别为0.8305、0.7794和0.9138
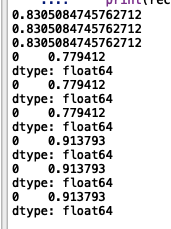
当
λ
=
1
\lambda=1
λ=1时,决策边界为

当
λ
=
0
\lambda=0
λ=0时,相当于不采用正则化,此时三种方法的精度、查准率和查全率均有所提高,(之前分别为0.8305、0.7794和0.9138)
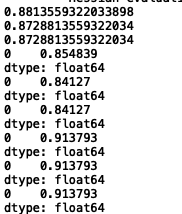
当
λ
=
0
\lambda=0
λ=0时,决策边界为

当
λ
=
10
\lambda=10
λ=10
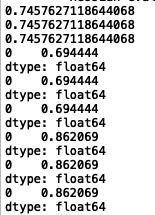

当
λ
=
100
\lambda=100
λ=100
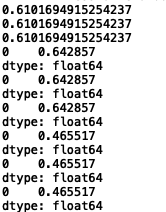

可以明显看出惩罚越大,其精度、查准率和查全率越低。对比以上 λ \lambda λ取0、1、10、100的情况,某种程度上说, λ = 1 \lambda=1 λ=1是比较合适的,既保证了精度、查准率和查全率相对较高,又提高了模型的泛化能力,一定程度上缓解了过拟合。






















 1236
1236











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








