文档级别事件论元抽取（2023第一篇）

Document-Level Event Argument Extraction by Leveraging Redundant Information and Closed Boundary Loss

摘要

文档级别的事件论元抽取，一个论元可能以不同的表述出现很多次（也就是同一个实体可能有多种提及）。论元丰富性是很有用的，但是经常被忽略。另外，Universum类是由很多没有典型共同特征的样本组成的，如果用交叉熵作为损失函数训练分类器，由于Universum的开放决策边界特征（该类中的样本分散，无明显边界），会使得有很多样本都被分到universum类中。基于此，再graph2token模块中构造了实体共指图，用于产出一个全面且有共指表示的图，另外一个实体总结图用于合并实体的多个提取结果。为了更好分类universum,提出利用封闭的边界构建了新的损失函数构造分类器。实验模型比之前的sota模型在F1上提升了3.35%。

1 Introduction

多余信息对于论元角色提取有好处也有问题：因为同一实体的不同提及会出现很多次，而且在不同位置提取实体的难度也不同，所以只要选择从简单的位置正确提取出就完成了任务，提升了模型健壮性并且任务难度降低。问题：多次出现不同representation如果只是简单地平均，会引入噪音。什么时候合并多种提取结果，什么时候不应该合并，需要算法进行解决。
提取论元可以看作是对候选论元的分类问题，大多数实体会被分为Universum,也就是交叉熵损失函数存在的open boundary问题。Universum类没有典型的共同特征，会分散在特征空间中。如果利用封闭域的分类器，错分类的情况可以得到更好的解决。

效果：sota,F1打败了最新的基线模型。和三种基线模型相比提升3.35%，5.27%,6.45%。

2 相关工作

讲了EAE（句子、文档级别）、封闭界限损失的相关工作。

3 方法

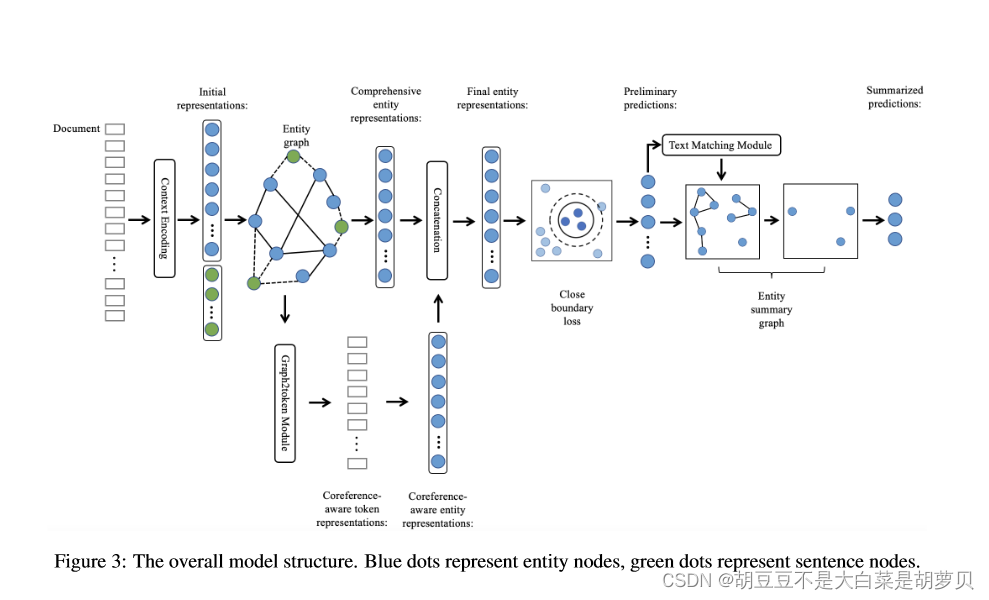
3.1 上下文编码

分别对句子和实体进行了编码，每个句子或实体的表示由memory（内部信息）和rule（上下文模式信息）组成。
D是经过Bi-LSTM编码后的token表示，n是文章长度，l是隐藏层维度。

e表示实体，s表示句子，memory表示实体或句子内部的信息，rule包含实体或句子外部的上下文信息。最终，实体和句子的表示是将memory和rule的部分连接起来。
这样做的原因是，类比人的记忆，记忆实体名称来预测memory representation，识别上下文模式来预测rule表示

3.2实体共指图

实体共指的作用有两方面，一方面持续增加对实体本身的理解；其次，识别出共指实体的内涵可以增加对共指实体上下文中的实体的理解。基于此，利用graph2token模块将全面的实体信息通过图结构反馈到token中，重构得到全面且 共指感知的实体表示。
之前的工作只是用graph 合并了同一实体的不同提及信息。这样就无法对上下文其他实体表示产生作用，因为其他实体初始化的时候就固定了表示。
graph2token将全面的实体信息（融合了共指的）反馈到token，重新得到全面(融合了上下文信息的)且共指感知（融合了共指的）的表示。

图构造

节点：实体节点、句子节点。
实体识别是利用Fisher的方法。
边：实体-实体边（使用SpanBert得到共指信息）实体-句子（实体所在句子）

图传播

图节点由实体节点和句子节点组成。
H ( n ) = { E , S } = { h 0 , h 1 , . . . , h p + q } ∈ R ( p + q ) × 2 l H(n)=\{E,S\}=\{h_0,h_1,...,h_{p+q}\}\in\mathbb{R}^{(p+q)\times2l} H(n)={E,S}={h0​,h1​,...,hp+q​}∈R(p+q)×2l
$h_i^{\prime }$是$i$节点所有邻居节点的 总表示，利用了GAT传播，汇总了$i$的所有邻居节点信息。

利用门控机制融合节点i的表示和其邻居节点总表示，也就是融合了共指信息，得到新的$i$节点表示:

总结：在图传播这一部分完成了节点融合了上下文的向量表示$h^{\prime \prime }$。

Graph2token

将共指实体的信息反馈到他们的邻居token中，得到共指感知的token表示$d_i^{\prime }$

利用共指感知的token表示构造共指感知的实体表示

最后，全面且共指感知的 实体表示：

3.3封闭边界损失

确定一个超球体内，目标类的样本在球内，Universum的在球体外，且不需要聚集在一起，允许其分散（与交叉熵不同的一点）。

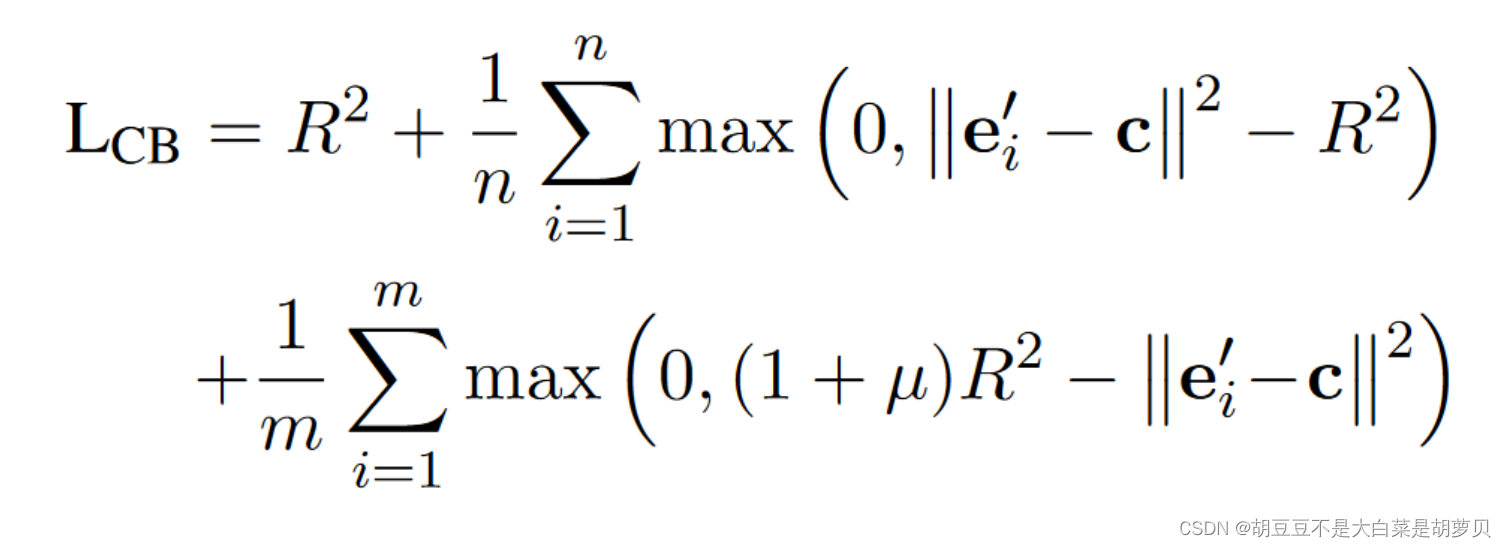
R²是为了最小化超球体的体积（类内越小越好），第二项是用超球体封住目标类样本，如果样本向量到中心点的欧式距离大于半径，则导致添加一个惩罚项，第三项是让unverse 样本屏蔽在超球体外，μ是调节封闭超球体和unversum样本间的距离，μ越大，距离越远。
分类：直接可以用于分类，不需再与交叉熵组合。如果实体的向量表示到中心的欧几里得距离小于半径，则g=1.
在最后作者提到，closed boundary loss是用于二分类的，提取论元是按照一次一个role的方法，这里为1表示是目标类，为0是不是该类。

3.4 实体总结图

利用文本匹配模块，从拼写和语义两个方面计算实体对间的相似分数。根据相似度分数构图，从各连通子图中选择一个具有最大权重和的节点作为子图的代表。最后这些节点就是最终的论元。

如果两个节点（实体提及）间的相似分数大于某个边界分数s,则这两个节点间存在边，且边的权重为相似度分数。从各连通子图中选择一个具有最大权重和的节点作为子图的代表。最后这些节点就是最终的论元表示。

实验

4.1 数据集

MUC-4数据集，共有1700篇文章，平均每个包含400个token7各段落。划分1300、200、200。perpetrator individual, perpetrator organization, target, victim, and weapon五类论元角色。

4.8Further Analysis

对于封闭边界的潜在用处：
1。closed boundary loss为分类器床在了一个封闭的决策边界，所以在处理测试集中没有见过的样例时也会有效果。
2.数据集市高度步平衡的，只有少数实体是论元，如果采用加权交叉熵，权重很难确定。但是封闭边界损失不需要调整权重，所以对不均衡的数据集也可行。
补充：加权交叉熵
用一个系数描述样本在loss中的重要性。如果是小数目样本，加强他对loss的贡献，对于大数目的样本减少对loss的贡献。
$loss=-\sum w\ast y_i\ast (log(logit{s}_i)+(1-y_i)\ast log((1-logit{s}_i)))$
其中$w$的计算:假设训练数据集有$M$类,每类的样本数目为$n_i$个，$i$从1到$M$。先求出$M$个样本数目的中位数，假设是$n_x$,所有$n_i$除以$n_x$,得到新的系数，这组系数取倒数，就得到了对应类别的系数。