深度学习基础知识_数学基础（学习笔记）

线性代数

向量、矩阵、矩阵计算，矩阵的秩，范数
了解更多可以参考: 哔哩哔哩: 晓之车高山老师 https://space.bilibili.com/138962930/channel/collectiondetail?sid=31387

1. 基本概念

• 标量（scalar）（0阶张量）：一个标量就是一个单独的数
• 向量（vactor）（1阶张量）：一个向量就是一列数
• 矩阵（matrix）（2阶张量）：矩阵是一个二维数组，其中的每一个元素被两个索引（而非一个）所确定
• 张量（tensor）：坐标超过两维的数组

2. 矩阵运算

• 转置：行变列，列变行

(1) 矩阵加法：

• 两个相同大小的矩阵，对应元素相加
  

(2) 矩阵乘法

结果中的aij=A的i行和B的j列对应相乘再相加


注：矩阵和自己不能直接相乘，需要对其中一个转置一下

(3) 逆矩阵运算

参考：https://www.bilibili.com/read/cv2920478

• 逆矩阵是什么：设A是数域上的一个n阶矩阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA=E ，则我们称B是A的逆矩阵，而A则被称为可逆矩阵。注：E为单位矩阵
• 逆矩阵的求法：待定系数法、 伴随矩阵法、 初等变换法
  例子：求下面三阶矩阵的逆矩阵
  $$\mathrm{A}=\left(\begin{array}{ccc}1& -4& -3\\ 1& -5& -3\\ -1& 6& 4\end{array}\right)$$

待定系数法求逆矩阵

待定系数法顾名思义是一种求未知数的方法。将一个多项式表示成另一种含有待定系数的新的形式，这样就得到一个恒等式。然后根据恒等式的性质得出系数应满足的方程或方程组，其后通过解方程或方程组便可求出待定的系数，或找出某些系数所满足的关系式，这种解决问题的方法叫做待定系数法。

伴随矩阵法求逆矩阵

1. 首先需要明确代数余子式是什么
   
2. 其次需要明确伴随矩阵是什么
   
3. 伴随矩阵求逆矩阵
   $${\mathrm{A}}^{-1}=\frac{1}{|\mathrm{A}|}{\mathrm{A}}^{\ast }$$
   其中|A|≠0，|A|为该矩阵对应的行列式的值
4. 行列式的求法
   （1）二阶行列式：主对角线元素积与副对角线元素积的差
   $$\mathrm{D}=\left|\begin{array}{cc}{\mathrm{a}}_{11}& {\mathrm{a}}_{12}\\ {\mathrm{a}}_{21}& {\mathrm{a}}_{22}\end{array}\right|={\mathrm{a}}_{11}{\mathrm{a}}_{22}-{\mathrm{a}}_{12}{\mathrm{a}}_{21}$$
   （2）三阶行列式：依然叫“对角线法则”，但更复杂
   $$\left|\begin{array}{ccc}\mathrm{x}& \mathrm{y}& \mathrm{z}\\ \mathrm{r}& \mathrm{s}& \mathrm{t}\\ \mathrm{a}& \mathrm{b}& \mathrm{c}\end{array}\right|=\mathrm{xsc}+\mathrm{rbz}+\mathrm{yta}-\mathrm{zsa}-\mathrm{yrc}-\mathrm{tbx}$$
   （3）多阶行列式：行列式等于其任意某行（或某列）的各元素与其对应代数余子式乘积之和
5. 例题的解法（伴随矩阵求逆矩阵）
   $$\mathrm{A}=\left(\begin{array}{ccc}1& -4& -3\\ 1& -5& -3\\ -1& 6& 4\end{array}\right)$$
   
   

初等变换法求逆矩阵

一般采用的是初等行变换

• 初等行变换是指以3种变换：
  ① A(i,j) → 交换 i ，j 两行
  ② A(i(k)) → 第 i 行乘以 k 得到
  ③ A(i,j(k)) → 第 j 行乘 k 加到第 i 行得到
• 先引入两个概念：
  • 行阶梯矩阵：
    • 全0行都在矩阵的底部
    • 每行最左边首个非零元素严格的比上面系数靠右
    • 首项系数所在列，在首项系数下面元素都是0
  • 行最简矩阵
    在行阶梯矩阵的基础上，非零行的第一个非零单元为1，且这些非零单元所在的列其他元素都是0
  • 可以证明：任意一个矩阵经过一系列初等行变换总能变成行阶梯型矩阵
    • 方法是一般从左到右，一列一列处理先把第一个比较简单的(或小)的非零数交换到左上角(其实最后变换也行)，用这个数把第一列其余的数消成零处理完第一列后，第一行与第一列就不用管，再用同样的方法处理第二列(不含第一行的数)
• 例题的初等行变换解法：
  

3. 矩阵的秩

• 在线性代数中，一个矩阵A的列（行）秩是A的线性独立的纵列（横行）的极大数目。即如果把矩阵看成一个个行向量或者列向量，秩就是这些行向量或者列向量的秩，也就是极大无关组中所含向量的个数。
• 求法: 用初等行变换把矩阵变成行阶梯形矩阵，行阶梯形矩阵中非零行的行数就是该矩阵的秩
• 矩阵A的秩(Rank) 记为r(A)
• 举例：
  • r(A) = 0的矩阵, 零矩阵
    
  • r(A) = 1的矩阵, 各行和各列成正比, 行向量和列向量的秩也是1
    

4. 特征值和特征向量

A是n阶方阵, 对于一个数λ, 存在非零列向量α, Aα = λα
则λ叫特征值, α叫特征向量, 且是对应于λ的特征向量
λ可以为0, 特征向量不能为0

实对称矩阵的不同特征值对应的特征向量是正交的

矩阵乘法即线性变换——对向量进行旋转和长度伸缩，效果与函数相同;
特征向量指向只缩放不旋转的方向;
特征值即缩放因子;
参考: https://zhuanlan.zhihu.com/p/353774689

5. 范数

向量范数，总体来讲，为表示向量长度的一种函数，为向量空间的所有向量赋予非零长度。

微积分基础

导数、梯度、泰勒展开

1. 导数

• 导数：曲线的斜率，反映曲线变化的快慢
  $${\mathrm{f}}^{{}^{\prime }}\left({\mathrm{x}}_0\right)=\underset{△\mathrm{x}\to 0}{\lim }\frac{\mathrm{f}\left({\mathrm{x}}_0+△\mathrm{x}\right)-\mathrm{f}\left({\mathrm{x}}_0\right)}{△\mathrm{x}}$$
• 常见函数的导数
  
• 高阶导数：导数的继续求导
• 偏导数：关于其中一个变量的导数，而保持其他变量固定

2. 梯度

• 一个函数对每一个自变量分别求偏导，这些偏导所构成的列向量就是梯度
  
  注：连续可微是指函数可以求导且导函数连续

• 梯度的方向是函数在该点变化最快的方向

• 梯度的维度和x分量的个数相同

• 举例
  

3. 泰勒公式

• 泰勒公式是在局部，用一个多项式函数，近似地替代，一个复杂函数.
• 如何通俗地理解泰勒公式：https://www.zhihu.com/question/21149770
• 泰勒公式的灵魂是导数值，而非幂函数。在展开的这一点，泰勒展开式与f(x)的每一阶导数值都完全相等。而这种“各阶导数值相等”，揭示了多项式函数和它想要替代的复杂函数f(x)在「每一个维度上完全相同」的奇妙的事实

4. 矩阵微分

多元微积分的一种表达方式，即使用矩阵和向量来表示因变量每个成分关于自变量每个成分的偏导数。

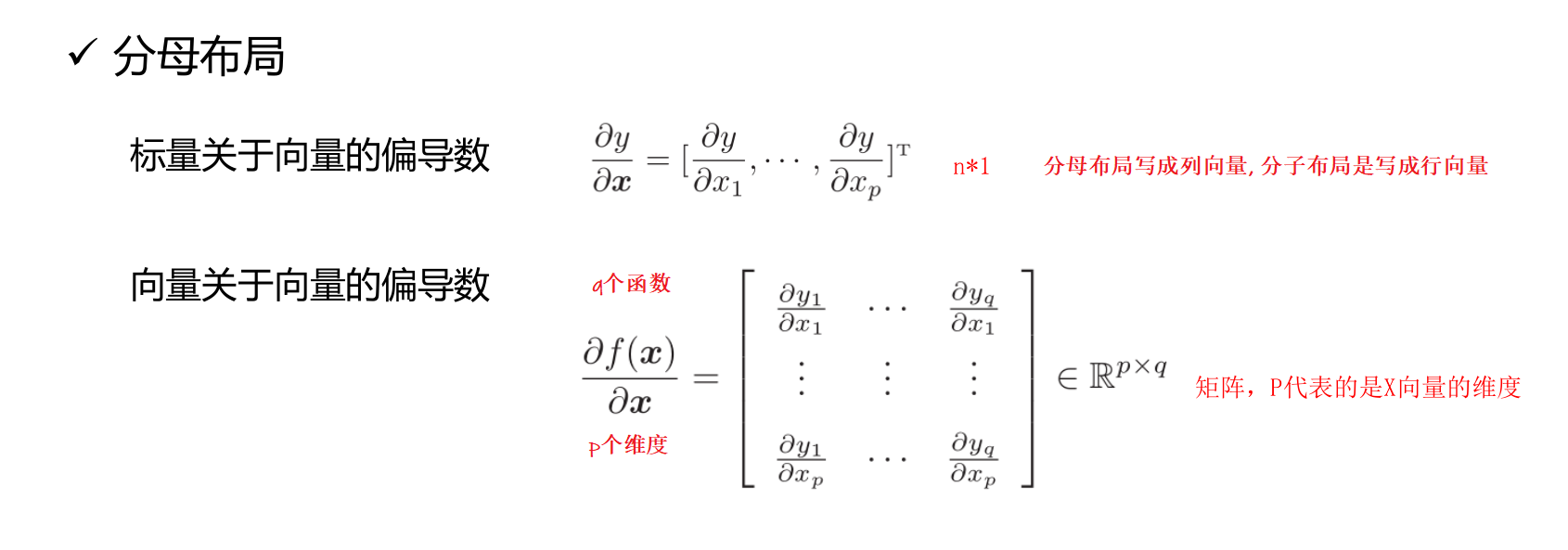
5. 微分链式法则

概率与统计基础

概率公式、常见分布、统计量

1. 概率公式

• 条件概率（后验概率）
  
  等号上面一个三角表示：定义为
• 贝叶斯公式（本质上也是条件概率）
  

2.1 一维随机变量及其分布

（1）随机变量

• 作用：把随机事件统一化，数字化
• 例子：把抛硬币为正面映射到数轴上的1
  随机变量是函数X=X(w)；如图所示：w的出现是有概率的，所以X的出现也是有概率的（其值随机会而定，故叫随机变量）
  

（2）分布函数

• 想用微积分做工具来研究随机变量，但是，w是事件，无法求导之类的，所以引入分布函数
• 分布函数是概率
  • 横坐标小x，纵坐标p概率
    
• 分布函数的性质
  a. F(x)单调不减
  b. 规定右连续：左空心，右实心，右极限值为函数值
  
  c.
  
  注：由a和c可得 0≤F(x)≤1，是有界函数
• 分布函数的应用：求概率
  

（3）离散型随机变量和连续型随机变量

• 离散型随机变量及其概率分布x~p_i(求和）
  
  分布函数：步步高的阶梯函数
• 连续性随机变量及其概率分布x~f(x) (积分）
  
• 离散和连续的对比
  
• 连续性随机变量在一点的事件是可能发生的 ，但是测不到，所以概率是0，左极限和右极限相等
  

2.2 常见分布

离散型（5个）

其中 0-1分布 和 二项分布 比较常见

1. 0-1分布，也叫Ber-E1（伯努利一次试验，伯努利分布），B(1,p)
   
   也可以写成：

2. 二项分布，B(n,p),也叫Ber-En（伯努利n次实验）

• p ≠（1-p）的二项分布图像
  
• p =（1-p）的二项分布图像
  

3. 泊松分布，某场合某单位时间内源源不断的质点来流的个数

k：欲知道概率的质点的个数，λ：强度
注：有时表示稀有概率发生的概率（青椒炒肉丝中肉丝有10根发生的概率，在食堂，λ₀小，在家λ₀大

4. 几何分布，G（p)，跟集合没有关系，Ber-E∞，首中即停止

5. 超几何分布H(n,N,M)古典概型的概率

连续型

接下来的分布都有自己的f(x)，而不是pi（离散）了

1. 均匀分布：uniform distribution，X~U(a,b)

• 一维几何概型（8点到九点任意时刻进入教室具有等可能性）
• 概率密度函数：（PDF）
  
  
  面积为1
• 分布函数：（CDF）
  
  规定等号跟着大于号
  
  f确定了可以确定F，F确定了，它的f不具有唯一性（可以在任意位置改成实心的，因为图像上任意扣个点不影响面积，测不出来）

2. 正态分布：X ~ N (µ, σ)

• 如果任何分布具有以下特征，则称为正态分布：
  1. 分布的均值、中位数和众数重合。
  2. 分布曲线呈钟形，关于线 x=μ 对称。
  3. 曲线下的总面积为 1。
  4. 恰好一半的值位于中心的左侧，另一半位于右侧。
• PDF（概率密度函数）：
  
  
  
• 标准正态分布：均值为0，标准差为1
  
  参考：https://www.analyticsvidhya.com/blog/2017/09/6-probability-distributions-data-science/#h2_4

3. Jensen不等式

• 凸函数：图中的不等式是Jensen不等式的两点形式
  
• Jensen不等式：上式的泛化形式

• 在概率论中的Jensen不等式：
  • 把λ_i看成取值为x_i的离散变量X的概率分布
    如果 X 是随机变量，g 是凸函数，则期望的函数 < 函数的期望
    
  • 对于连续变量，Jensen不等式给出了积分的凸函数值和凸函数的积分值间的关系：
    

4. 大数定理

大数定理简单来说，指的是某个随机事件在单次试验中可能发生也可能不发生，但在大量重复实验中往往呈现出明显的规律性，即该随机事件发生的频率会向某个常数值收敛，该常数值即为该事件发生的概率。

另一种表达方式为当样本数据无限大时，样本均值趋于总体均值。

因为现实生活中，我们无法进行无穷多次试验，也很难估计出总体的参数。

大数定律告诉我们能用频率近似代替概率；能用样本均值近似代替总体均值
参考：https://zhuanlan.zhihu.com/p/77312635

5. 随机过程

若一随机系统的样本点是随机函数，则称此函数为样本函数，这一随机系统全部样本函数的集合是一个随机过程。
实际应用中，样本函数的一般定义在时间域或者空间域。随机过程的实例如股票和汇率的波动、语音信号、视频信号、体温的变化，随机运动如布朗运动、随机徘徊等等。

6. 信息熵

• 信息熵越大，事件不确定性就越大
• 信息熵其实从某种意义上反映了信息量存储下来需要多少存储空间
• 根据真实分布，我们能够找到一个最优策略，以最小的代价消除系统的不确定性（比如编码），而这个代价的大小就是信息熵
  参考：https://charlesliuyx.github.io/2017/09/11/%E4%BB%80%E4%B9%88%E6%98%AF%E4%BF%A1%E6%81%AF%E7%86%B5%E3%80%81%E4%BA%A4%E5%8F%89%E7%86%B5%E5%92%8C%E7%9B%B8%E5%AF%B9%E7%86%B5/

7. 统计学习和机器学习区别

• 统计学习：对历史数据做关系分析
• 机器学习：对未来数据预测（基于统计学习，但同时解决统计学习的过拟合问题）