AVL树

数据结构 -文泉学堂 课程链接

二叉搜索树

BST在二叉树的形式基础上借鉴了有序向量的特点。对有序向量的借鉴多体现在BBST。

• 循关键码访问call-by-key：数据项之间，依照各自的关键码彼此区分，关键码之间可进行大小比较以及相等比对。以下将数据集中的数据项统一表示为词条entry。
  词条应包含：模板类、关键码、键值、默认构造函数、克隆函数、比较器、判等器，并将磁条的比较转化为key的比较。
• 顺序性：任一节点均不大于其父节点。
• 单调性：BST的中序遍历必单调且非降。

查找

采用分而治之的策略，逐步缩小搜索范围，直至找到。

template<typename T> BinNodePosi(T) & BST<t>::search(const T &e)//对外接口
{
    return searchIn(_root, e, _hot=NULL);
}
static BinNodePosi(T) & searchIn(BinNodePosi(T) &v, const T & e, BinNodePosi(T) &hot)//当前子树根，目标关键码、记忆热点
{
    if(!v || (e == v->data)) 
        return v;
    hot = v;
    return searchIn((e < v->data ? v->lchild : v->rchild), e, hot);
}

时间复杂度不超过O（n）。
返回值语义：

• 成功时，返回一个关键吗为e且存在的节点
• 失败时，返回最后一次试图转向的空节点nullptr

_hot变量语义：

• 失败时，假象将空节点转换为一个关键码为e的哨兵节点
• 无论成功与否，_hot总指向命中节点的父节点，返回值总是指向命中节点

插入

由于调用searchIn函数后，其返回值正是我们将要插入元素的位置（假设无重复节点），则我们将待插入元素封装为一个节点，将返回值引用指向该节点。

template<typename T>BinNodePosi(T) BST<T>::insert(const T &e)
{
    BinNodePosi(T) &x=search(e); //查找目标，留意_hot位置
    if(!x)
    {
        x=new BinNode<T>(e._hot); //在x出创建节点，以_hot为父节点
        _size++;
        updateHeightAbove(x);
    }
    return x;
}

删除

template<typename T>bool BST<T>::remove(const T &e)
{
    BinNodePosi(T) &x=search(e); //定位目标节点
    if(!x) //确认目标存在
        return false;
    removeAt(x,_hot); //两类情况删除
    _size--;
    updateHeightAbove(_hot); //更新_hot以及树高
    return true;
}

情况一

目标节点至多只有一颗子树，删除节点，用其子树根节点代替节点位置。

template<typename T>static BinNodePosi(T) removeAt(BinNodePosi(T) &x, BinNodePosi(T) hot)
{
    BinNodePosii(T) w=x; //实际被摘除节点
    BinNodePosi(T) succ=NULL; //实际被摘除节点接替者
    if      (!HasLChild(*x)) succ=x=x->rchild;
    else if(HasRChild(*x)) succ=x=x->rchild;
    else{ /* 左右子树均存在 */}
    hot=w->parent; //记录实际被摘除节点的父节点
    if(succ) succ->parent=hot; //将接替者与hot相连
    release(w->data); //释放被摘除节点
    release(w);
    return succ;
}

情况二

目标节点有两颗子树。将情况转化为情况一。
接口BinNode::succ();返回当前节点的直接后继，其思路是在当前节点右孩子存在的情况下，从右孩子的左孩子进入不断访问其左孩子，直至左孩子不存在，直接后继指不小于当前节点的最小节点。

思想：将待删除节点与其直接后继交换，再删除交换后的但删除节点，此时与情况一一致。

else
{
    w=w->succ();
    swap(x->data,w->data);
    BinNodePosi(T) u=w->parent;
    (u==x ? u->rChild : u->lChild) = succ =w->rChild;
    //u==x，即是待删除节点的直接后继就是他的右孩子的情况
}

平衡与等价

BST的平均树高为

O (logn)

为了更快的搜索速度，我们要尽可能的缩小树高，当节点数目相同时，兄弟子树的高度越接近，全树的树高也就越小。但BST树的最小高度不低于

O(long[2]n)

也称上述树高为理想平衡，但理想平衡难以达到，且维护成本极高。

旋转变换

经过某种改变BST的拓扑结构，但变换后的树与之前的树等价。

AVL树 一种BBST

定义平衡因子，balFac(v) = height(lc(v)) - height(rc(v))即是左子树与右子树高度之差。
根据AVL树的定义，有

\forall[v],    |balFac(v)| <=1

高度为h的AVL树，至少包含下述个节点。

S(h) = fib(h+3)-1

AVL树接口

#define Balanced(x) stature(x.lChild)=stature(x.rChild) //理想平衡
#define BalFac(x) stature(x.lChild)-stature(x.rChild) //平衡因子
#define AvlBalanced(x) (-2<BalFac(x)) && (BalFac(x)<2)
template<typename T>class AVL: public BST<T>
{
public:
    BinNodePosi(T) insert(const T &);
    bool remove(const T &);
}

失衡与重平衡

删除节点至多只会导致一个祖先节点失衡。

插入后重平衡

单旋

同时有多个失衡节点，但最低者g不低于x的祖父。做一次zig或者zag操作。

• 1）创建临时变量p
• 2）使p的左子树成为g的右子树
• 3）使g成为p的左子树
• 4）使子树根指向p
• 5）释放临时引用

在局部恢复平衡后，其他失衡节点也会重平衡。
单旋只涉及局部常数个节点，其时间复杂度为O（1）。

双旋

同时有多个失衡节点，但最低者g不低于x的祖父。做两次zig或者zag操作。

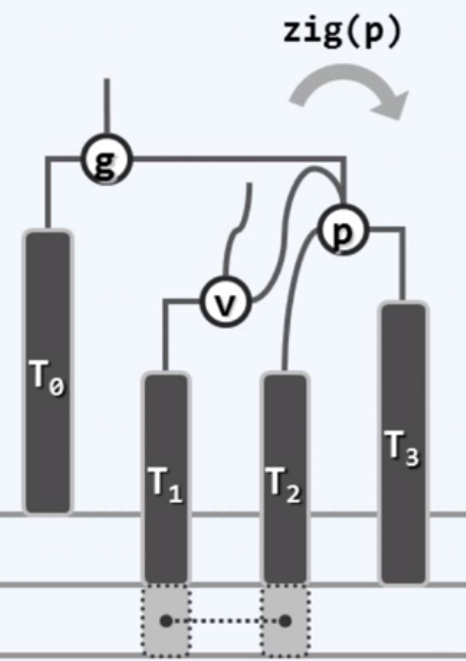
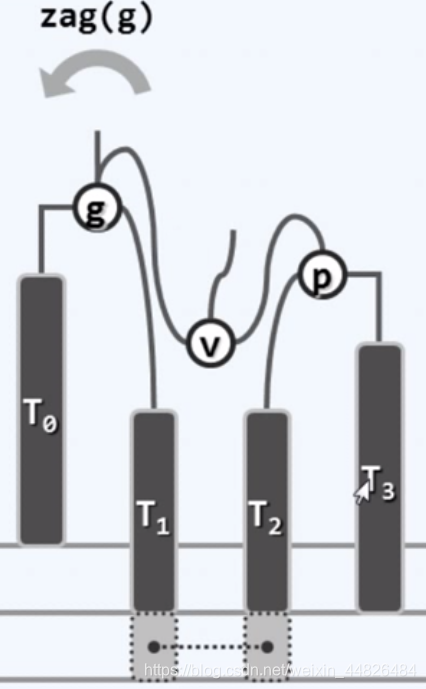
• 1）创建临时变量v
• 2）使v的右子树成为p的左子树
• 3）使p的左子树成为v的右子树
• 4）使p成为v的右子树
• 5）使v的左子树成为g的右子树
• 6）使g成为v的左子树
• 7）使v成为子树根
• 8）释放临时引用

算法实现

template<typename T> BinBodePosi(T) AVL<T>::insert(const T &e)
{
    BinNodePosi(T) &x=search(e);
    if(x)  //若目标尚不存在
        return x;
    x=new BinNode<T>(e, _hot);
    _size++;
    BinNodePosi(T) xx=x;  //则创建x
    for(BinNodePosi(T) g = x->parent; g; g=g->parent) //从x出发，逐层向上检查各代祖先g
    {
        if(!AVLBalanced(*g)  //发现失衡，则恢复
        {
            FromParentTo(*g) = rotateAt(tallerChild(tallChild(g)));
            break;
        }
        else  //否则，在仍然平衡的祖先处恢复高度
        updateHeight(g);
    }
    return xx;
}

删除后重平衡

单旋

同时至多只有一个失衡节点，首个有可能的即是x的父节点_hot。
如下图所示，若g,p,v三代节点按同一方向排列，删除T3最底层节点，则需对节点g做zig（或zag）旋转。
其中T0和T1的最底层叶子至少存在一个，T2最底层叶子可存在或不存在。

观察可知，做旋转操作后，子树的树高又T2的最低成叶子是否存在决定，若存在，则子树的整体树高不变，若不存在，则导致子树的树高-1，此时，子树的祖先节点可能由于本次旋转操作而失衡。
因为上述的失衡传播现象，可能要做O（logn）次调整（对每一层进行一次调整），这是删除操作的特点。

双旋

同时至多只有一个失衡节点，首个有可能的即是x的父节点_hot。
如下图所示，若g,p,v三代节点按之字形排列，删除T3最底层节点，则需对节点g做zagzig（或zagzig）旋转。
其中T0和T1的最底层叶子至少存在一个。

可以发现，经过双旋之后，子树整体的高度缩小了一层，则导致这棵子树的所有祖先节点都可能发生了失衡，可能要做O（logn）次调整（对每一层进行一次调整）。

算法实现

tepmlate<typename T> bool AVL::remove(const T &e)
{
    BinNodePosi(T) &x=search(e);
    if(!x)  //若目标的确存在
        return fasle;
    removeAt(x, _hot);  //则在BST规则删除之后，_hot及祖先均有可能失衡 
    size--;
    //从_hot出发逐层向上，依次检查各代祖先g
    for(BinNodePosi(T) g=_hot; g; g=g-<parent)
    {
        if(!AVLBalanced(*g))  //发现失衡，则进行重平衡
            g=FromParentTo(*g)=rotateAt(tallerChild(tallerChild(g)));
        updateHeight(g);  //并更新高度
    }  //可能需要做O（logn）次调整全树高度可能下降
    return true;
}

3+4重构

考虑到rotateAt(x,_hot)按照前述的算法也可以进行实现，但我们考虑更多的是是全树平衡，为此，我们考虑对树进行重构，而不是直接进行繁琐的旋转。
设g(x)为最低的失衡节点，考察期祖孙三代g_pv,按中序遍历的次序，将其重命名为a<b<c。
可知，他们最多拥有四棵（可能为空）不相交的子树，按中序遍历将它们重命名为T0<T1<T2<T3。
观察插入单旋、双旋，删除单旋、双旋可知，我们做的重平衡操作，都是将局部子树的形式转化为下图的形式。

则我们可以直接对局部子树进行重构，使其满足上述形式。

3+4重构实现

template<typename T> BinNodePosi(T) BST<T>connect34(
    BinNodePosi(T) a, BinNodePosi(T) b, BinNodePosi(T) c, 
    BinNodePosi(T) T0, BinNodePosi(T) T1, BinNodePosi(T) T2, BinNodePosi(T) T3)
{
    a->lChild = T0;  if(T0) T0->parent = a;
    a->rChild = T1;  if(T1) T1->parent = a;  updateHeight(a);
    c->lChild = T2;  if(T0) T2->parent = c;
    c->rChild = T3;  if(T1) T3->parent = c;  updateHeight(c);
    b->lChild = a;  a->parent = b;
    b->rChild = c;  c->parent = b;  updateHeight(b);
    return b;
}

rotateAt

为完成重构操作，我们还需做的准备是对3+4个元素进行正确的重命名。

//传入参数只有孙子节点v
template<typename T> BinNodePosi BST<t>::rotateAt(BinNodePosi(T) v)
{
    BinNodePosi(T) p=v->parent；  //父节点
    g=p->parent;  //祖父节点
    if(IsLChild(*p))  //zig
        if(IsLChild(*v))  //zigzig
        {
            p->parent=g->parent;  //向上链接，更新后子树根为p
            return connect(v, p, g, v->lChild, v->rChild, p->lChild, p->rChild);
        }
        else  //zigzag
        {
            v->parent=g->parent;  //向上链接，更新后子树根为v
            return connect(p, v, g, p->lChild, v->lChild, v->rChild, g->rChild);
        }
    else //zag
    {
        if(IsRChild(*v))  //zagzag
        {
            p->parent=g->parent;  //向上链接，更新后子树根为p
            return connect(g, p, v, g->lChild, p->lChild, v->lChild, v->rChild);
        }
        else  //zagzig
        {
            v->parent=g->parent;  //向上链接，更新后子树根为v
            return connect(g, v, p, g->lChild, v->lChild, v->rChild, p->rChild);
        }
    }
}

AVL总体评价

• 优点：无论查找、插入、删除，最坏情况下的复杂度为O(logn),O(n)的存储空间。
• 缺点：借助高度或平衡因子，为此需改造元素结构，或额外封装。实测复杂度与理论值尚有差距，插入\删除后的维护成本不菲，频繁的插入\删除操作使得得不偿失。
  单次动态调整后，全树的拓扑结构的变化量可能高达O(longn)。