【快速理解和上手】逻辑回归logistic regression （无原理，只有公式化步骤）

逻辑回归 Logistic regression

目的：解决二分类问题
数学效果：根据数据$(\vec{x},y)$ （其中y为0或1），拟合一条曲线，x轴表示特征，y轴表示一个概率，即这个输入 $x$ 对应着类别为正类的概率。

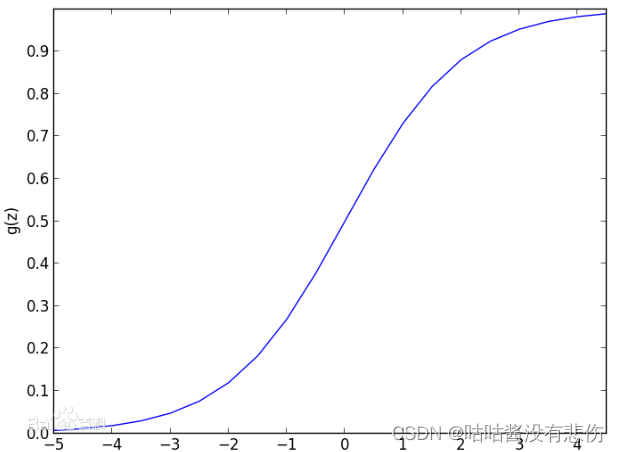
Logistic函数

逻辑回归是一种广义线性回归。
我们知道线性回归直接将 $\vec{w}\cdot \vec{x}+b$ 作为因变量，即 $y=\vec{w}\cdot \vec{x}+b$

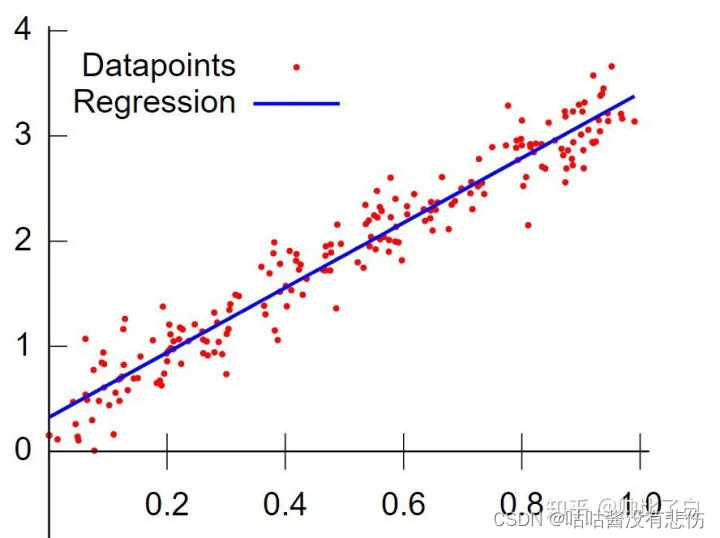
而logistic回归则通过函数 $g(z)$ 将 $z=\vec{w}\cdot \vec{x}+b$ 映射到一个概率 $y\in (0,1)$，$y=g(\vec{w}\cdot \vec{x}+b)$，然后根据 $y$ 的大小是否大于决策边界（一般取0.5）来决定预测值。
如果 $g$ 是logistic函数，就是logistic回归；如果 $g$ 是多项式函数（$g(z)=a_{1}z+a_2{z}^2+....+a_n{z}^n+c$），就是多项式回归。

那么我们的logistic函数长什么样呢?
logistic函数：
$$y=\frac{1}{1+e^{-z}}$$
将$z=\vec{w}\cdot \vec{x}+b$ 带入上式，因变量的名字换成 f，就得到了逻辑回归模型：
$$f_{\vec{w},b}(x)=\frac{1}{1+e^{-(\vec{w}\cdot \vec{x}+b)}}$$

理解logistic回归的输出

咱不想深入理解最大似然的推导过程，只要记住输出表示一个概率，即输入 $x$ 对应着类别为正类的概率，即可。
用数学语言描述就是一个条件概率：
$$f_{\vec{w},b}(x)=P(y=1|\vec{x};\vec{w},b)$$
其中那个分号($;$)后面的$\vec{w},b$，是指 $\vec{w}$ 和 $b$ 是影响计算的参数，分号前面 $\vec{x}$ 的才是条件概率的前提条件。

那么我们接下来要做的，就是求解这个模型$f_{\vec{w},b}(x)=\frac{1}{1+e^{-(\vec{w}\cdot \vec{x}+b)}}$，也就是求得最佳参数$\vec{w}$，使得拟合效果最好（即损失函数值最小）

决策边界 decision boundary

我们的目的是分类，也就是这个x属于正类1还是负类0，那么就需要确定一个决策边界值，当输出超过这个决策边界值，就归为正类1；反之，为负类0。一般这个决策边界取0.5。

损失函数（代价函数） loss function

在线性回归中，我们使用均方差作为损失函数：（m个样本）
$$J(\vec{w},b)=\frac{1}{m}\sum _{i=1}^m\frac{1}{2}(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}{)}^2$$
可否也用均方差作为逻辑回归模型的损失函数呢？不可以。因为损失函数需要是一个凸函数，这样才可以用梯度下降法进行优化，找到使得损失最小的那个参数。但如果对 $f_{\vec{w},b}=\frac{1}{1+e^{-(\vec{w}\cdot \vec{x}+b)}}$ 使用均方差，得到的函数不是一个凸函数，它有很多的局部最小值，不好用梯度下降法优化。

逻辑回归模型的一种常用的损失函数叫做log损失，
对于第 $i$ 个样本，用$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})$ 表示其损失：
$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=-y^{(i)}log(f_{\vec{w},b}({\vec{x}}^{(i)}))-(1-y^{(i)})log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))$$
长得挺奇怪哈，不慌，分开看。当训练数据的标签 $y^{(i)}=1$，$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=-1\ast log(f_{\vec{w},b}({\vec{x}}^{(i)}))$$它是凸的，长这样：（因为 f 的值在0~1之间，所有只看横轴[0,1]对应的这一段就行）

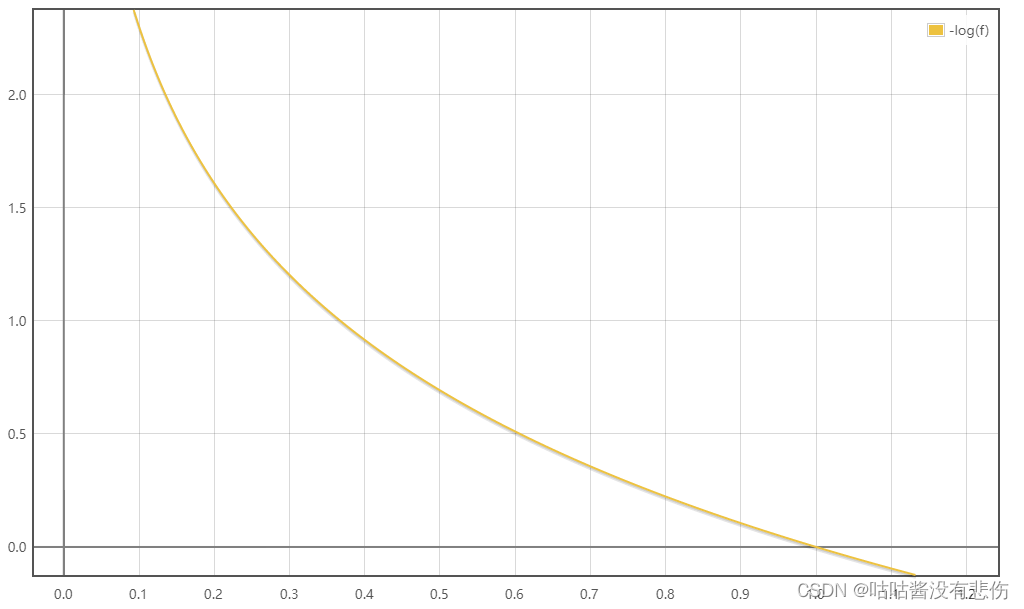
从图像上看，也符合损失函数的基本素养：当训练数据的标签 $y^{(i)}=1$时，预测值越接近1，loss越小。
当训练数据的标签 $y^{(i)}=0$，$$L(f_{\vec{w},b}({\vec{x}}^{(i)}),y^{(i)})=-1\ast log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))$$
它也是凸的，长这样：（因为f的值在0~1之间，所有只看横轴[0,1]对应的这一段就行）

从图像上看，也符合损失函数的基本素养：当训练数据的标签 $y^{(i)}=0$时，预测值越接近0，loss越小。
以上是单个样本的损失，对于整个训练集，损失就是单个损失的平均值，所以逻辑回归损失函数：
$$J(\vec{w},b)=-\frac{1}{m}\sum _{i=1}^m{y}^{(i)}log(f_{\vec{w},b}({\vec{x}}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))$$
有了损失函数，下一步就是求解合适的参数值，使得损失函数最小。我们使用梯度下降法。

梯度下降

梯度下降的原理也不详细展开了，反正我们知道过程就是每次对w和b求偏导，然后让w和b分别减去偏导值乘以学习率。
$$\begin{gathered} w_j=w_j-\alpha \frac{\partial }{\partial w_j}J(\vec{w},b) \\ b=b-\alpha \frac{\partial }{\partial b}J(\vec{w},b) \end{gathered}$$

这两个更新是同时进行的。
把偏导代入，就是
$$\begin{gathered} w_j=w_j-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)} \\ b=b-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}) \end{gathered}$$

其中$$f_{\vec{w},b}(x)=\frac{1}{1+e^{-(\vec{w}\cdot \vec{x}+b)}}$$
不断重复这个过程就好啦，

过拟合与欠拟合

欠拟合—— bias偏差 高。表现为那个函数
过拟合——variance方差 高，泛化性generation差

解决过拟合

1. 使用更多的数据
2. 选择更少的特征 feature selection
3. 正则化 regularization，下文详细说明

正则化

是一种更温和地减少参数的方法，本质是鼓励算法缩小高维参数的值

logistic回归带正则化的损失函数$$J(\vec{w},b)=-\frac{1}{m}\sum _{i=1}^m{y}^{(i)}log(f_{\vec{w},b}({\vec{x}}^{(i)}))+(1-y^{(i)})log(1-f_{\vec{w},b}({\vec{x}}^{(i)}))+\frac{\lambda }{2m}\sum _{j=1}^n{w}_j^2$$
n是特征数量，第二个加数项就是正则项，$\lambda$是正则化系数，$\lambda$越大，函数越不会过拟合越接近欠拟合；$\lambda$越小，正则化的效果越差，函数越接近过拟合。

梯度下降
因为加入了正则项，所以梯度下降的偏导有所变化，但只表现在对w的的偏导上
$$\begin{gathered} w_j=w_j-\alpha [\frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{w}_j] \\ b=b-\alpha \frac{1}{m}\sum _{i=1}^m(f_{\vec{w},b}({\vec{x}}^{(i)})-y^{(i)}) \end{gathered}$$

根据梯度下降公式，我们经过多轮迭代，当损失值足够小，就训练出了最合适的参数了。那么这个logistic回归模型就求解出来了。